Genere sus propios datos estadísticos Teach article
¿Qué preferirían sus estudiantes, cultivar plantas comestibles o trabajar con estadísticas? A continuación, se describe una forma de combinar estas actividades en una aplicación de análisis estadístico en un caso práctico real.
La mayoría de los estudiantes de biología prefieren evitar las matemáticas, pues a menudo ésa es una de las razones por las que eligieron la biología. Por eso, en las clases de último año (de 16 a 18 años), cuando se anuncian las pruebas estadísticas, toda la clase se queja, y muy a menudo también el profesor.

siempre es el aspecto que
más interesa a los estudiantes
Sean/Flickr CC BY-ND 2.0
En 2018, llevamos a cabo un proyecto en nuestra escuela en Kazajstán, cultivando plantas en el invernadero de la escuela con algunas de las clases de Secundaria. Al mismo tiempo, los estudiantes de biología de Bachillerato estaban estudiando la prueba t, que es una forma estándar de evaluar una hipótesis experimental. Introducir las matemáticas en las lecciones de biología no es fácil, por lo que se nos ocurrió que podría ser más interesante utilizar los datos recopilados en el proyecto de cultivo de plantas para hacer algunos análisis de datos de la vida real.
La prueba t es una de las distintas pruebas estadísticas estándar que se utilizan para conocer si existe una diferencia «estadísticamente significativa» entre dos conjuntos de datos relacionados, es decir, si tal diferencia podría haber ocurrido por casualidad. El cultivo de plantas en dos condiciones diferentes, en suelo normal y en suelo enriquecido, puede proporcionar una hipótesis a verificar y dos conjuntos de datos relevantes para el análisis estadístico.
La idea fue un éxito: nos hemos dado cuenta que el uso de datos de un experimento realizado en la escuela hacía que el análisis estadístico pareciera más real, y los estudiantes han podido comprobar cómo la prueba t nos permite sacar conclusiones en la vida cotidiana, en lugar de ser simplemente un ejercicio realizado en una hoja de papel.
En este artículo describimos las dos etapas de esta actividad: el proyecto de invernadero y el posterior análisis estadístico mediante la prueba t. La actividad de invernadero es adecuada para estudiantes de 14 a 16 años y tiene una duración de alrededor de ocho horas de clase, más 10 a 12 semanas para que las plantas crezcan. La actividad de la prueba t es adecuada para estudiantes de 16 a 18 años y dura unas cuatro horas.
Para algunas definiciones de términos estadísticos, consulte el cuadro de texto (o utilice fuentes estándar).

Joanne Brown
Etapa 1: Cultivo de plantas en invernadero

enriquecidas (arriba) son de
color más claro que las
parcelas normales (abajo).
Joanne Brown
A la mayoría de los estudiantes les gusta ver crecer las plantas, por lo que el experimento de horticultura es una actividad interesante en sí misma. Kazajstán tiene un clima continental, con veranos muy calurosos e inviernos extremadamente fríos, por lo que para cultivar plantas en la primavera usamos un invernadero con calefacción. Por supuesto, las plantas también se pueden cultivar al aire libre si la temporada y el clima son adecuados.
Lo más importante es elegir una hipótesis clara y dos condiciones de crecimiento claramente distintas para probar la hipótesis. Elegimos lo siguiente:
Objetivo del experimento: determinar si enriquecer el suelo con nutrientes aumenta el crecimiento de las hojas de rábano.
Hipótesis: las plantas de rábano que crecen en un suelo enriquecido con nutrientes tendrán hojas más grandes.
Para enriquecer el suelo, le agregamos estiércol de corral con potasio (1,3%), nitrógeno (0,1%) y magnesio (0,6%).
Materiales
- Semillas de rábano (aproximadamente 160 en total, o 10 semillas por parcela)
- Superficie de suelo normal para la siembra, al menos 16 m2
- Estiércol de corral (4 kg en total o 500 g por parcela)
- Palas
- Regadera
- Cinta métrica
- Regla
- Calculadora
Procedimiento
Los estudiantes pueden realizar las siguientes tareas para cultivar las plantas.
Nota de seguridad:
Lavarse siempre las manos después de manipular tierra o estiércol.
1. Para preparar la tierra, use la pala para cavar y darle muchas vueltas hasta que esté suelta y sin terrones.
2. Mida 16 parcelas de 1 m2 cada una con la cinta métrica: ocho para el suelo a enriquecer y ocho para el suelo normal. Delimite las parcelas con una cuerda, luego etiquete cada una con el número de parcela.
3. Añada 500 g de estiércol de corral a cada una de las ocho parcelas a enriquecer. Use las palas para mezclar el estiércol con la tierra.
4. Plante diez semillas de rábano por parcela, aproximadamente a 100 mm de distancia y 10 mm de profundidad.
5. Riegue las plantas todos los días o según sea necesario. Observe el crecimiento de las plantas durante aproximadamente siete semanas, desde la germinación hasta las plántulas y luego hasta las plantas completamente desarrolladas.
6. Un día a la semana (por ejemplo, viernes) durante el período de crecimiento, use una regla para medir la longitud de la hoja más grande de cada planta en las 16 parcelas. Registre estas medidas con cuidado.
Al final del período de crecimiento, calcule la longitud media (promedio) de estas hojas para cada parcela durante todo el período de crecimiento. Esto se calcula sumando todas las medidas de ese gráfico y luego dividiendo el resultado por el número de medidas.

Joanne Brown
Resultados y conclusiones
En nuestro experimento, 67 plantas de rábano germinaron en las parcelas con el suelo enriquecido y 99 plantas de rábano germinaron en el suelo normal (los números diferían porque fue difícil contar todas las semillas con precisión, además algunas semillas no germinaron).
La siguiente tabla muestra las longitudes medias de las hojas más grandes de las plantas en cada parcela durante el período de crecimiento y la media general en cada condición.
| Suelo enriquecido: Números de las parcelas | Longitud media de la hoja más grande de las plantas en cada parcela (mm) | Suelo normal: Números de las parcelas | Longitud media de la hoja más larga de las plantas en cada parcela (mm) | |
|---|---|---|---|---|
| 1 | 39 | 9 | 38 | |
| 2 | 45 | 10 | 41 | |
| 3 | 41 | 11 | 43 | |
| 4 | 46 | 12 | 39 | |
| 5 | 45 | 13 | 37 | |
| 6 | 48 | 14 | 38 | |
| 7 | 39 | 15 | 41 | |
| 8 | 44 | 16 | 36 | |
| Media general (suelo enriquecido) | 43.38 | Media general (suelo normal) | 39.13 |
Como muestran estos resultados, las hojas eran en promedio más grandes en las parcelas con los nutrientes añadidos, en línea con nuestra hipótesis.
Para una clase de Secundaria, es suficiente concluir diciendo que este resultado concuerda con la hipótesis. Sin embargo, en una clase de Bachillerato (y en ciencia real), tendríamos que demostrar que es poco probable que este resultado haya ocurrido por casualidad, en otras palabras, que es estadísticamente significativo. Este es el objetivo de la siguiente etapa de la actividad.
Etapa 2: Uso de la prueba t
Los resultados del experimento de horticultura se pueden utilizar como datos «reales» para que los estudiantes avanzados los analicen mediante la prueba t.
La prueba t se utiliza para determinar si existe una diferencia estadísticamente significativa (es decir, no aleatoria) entre las medias de dos conjuntos de datos relacionados y, por tanto, entre los resultados de dos condiciones experimentales diferentes. En este caso, los estudiantes investigan si el enriquecimiento del suelo ha supuesto una diferencia estadísticamente significativa en el tamaño de las hojas de rábano, en comparación con el suelo normal, o si la diferencia en el tamaño medio de las hojas podría haber ocurrido por casualidad.
Procedimiento
Para usar la prueba t, necesitamos los dos conjuntos de datos del experimento (suelo normal y enriquecido). Luego seguimos un proceso matemático estándar para analizar los datos y averiguar si respaldan nuestra hipótesis elegida.
Paso 1: Decidir sobre la hipótesis nula, H0
Para averiguar mediante la prueba t si una hipótesis está respaldada por datos, primero debemos decidir sobre una «hipótesis nula». En general, esta es la hipótesis de que las diferentes condiciones no influyeron en los resultados. Entonces, si el análisis de datos muestra que podemos rechazar esta hipótesis, entonces podemos concluir que las diferentes condiciones sí dieron lugar a obtener resultados diferentes.
Aquí, la hipótesis nula, H0, es:
No habrá una diferencia significativa en el tamaño promedio de las hojas de rábano que crecen en suelo enriquecido y las que crecen en suelo normal.
Paso 2: Calcular la desviación estándar en cada caso
A continuación, calculamos la desviación estándar (DE) para cada uno de los dos conjunto de datos.
Desviación estándar (DE) =
Donde:
 x = medida media para cada parcela de suelo (ver tabla 1)
x = medida media para cada parcela de suelo (ver tabla 1)
x̅ = promedio de las medias de todas las mediciones en una condición (suelo enriquecido, suelo normal); ver tabla 1
n = número de medidas in cada condición (8 en este caso)
Por ejemplo, en la parcela 1:
x = 39
x̅ = 43.38
Entonces (x – x̅)2 = (39 – 43.38)2 = 19.18
Los resultados completos se muestran en la tabla 2.
| Número de parcela | Suelo enriquecido, tamaño de las hojas (mm) | (x – x̅)2
x̅ = 43.38 |
NÚMERO DE PARCELA | Suelo normal, tamaño de las hojas (mm) | (x – x̅)2
x̅ = 39.13 |
|
|---|---|---|---|---|---|---|
| 1 | 39 | 19.18 | 9 | 38 | 1.28 | |
| 2 | 45 | 2.62 | 10 | 41 | 3.50 | |
| 3 | 41 | 5.66 | 11 | 43 | 14.98 | |
| 4 | 46 | 6.86 | 12 | 39 | 0.02 | |
| 5 | 45 | 2.62 | 13 | 37 | 4.53 | |
| 6 | 48 | 21.34 | 14 | 38 | 1.28 | |
| 7 | 39 | 19.18 | 15 | 41 | 3.50 | |
| 8 | 44 | 0.38 | 16 | 36 | 9.80 | |
| Totale | 77.84 | Totale | 38.89 |
Entonces, la desviación estándar para el suelo enriquecido (DE1):
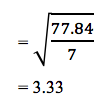
La desviación estándar para el suelo normal (DE2):
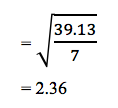
Paso 3: Calcular el valor t general
Para calcular el valor de t utilizamos la ecuación siguiente
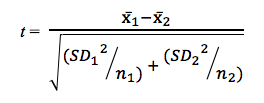
Donde:
x̅1= media de los resultados en la primera condición (suelo enriquecido)
x̅2 = media de los resultados en la segunda condición (suelo normal)
n1 = número de medidas en la primera condición
n2 = número de medidas en la segunda condición
Entonces:
x̅1 – x̅2 = 43.48 – 39.13
= 4.25
DE12= 3.332 = 11.09
DE22 = 2.362 = 5.57
n1 = n2 = 8
11.09/8 = 1.39
5.57/8 = 0.70
Resultando
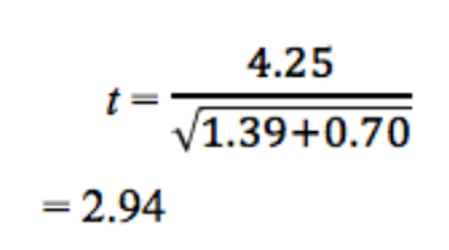
En los siguientes pasos, usaremos esta valor de t para averiguar si los datos apoyan la hipótesis nula o si debemos rechazarla.
Paso 4: Encontrar los ‘grados de libertad’
Los «grados de libertad» en un cálculo estadístico es un concepto matemático que representa cuántos valores involucrados en un cálculo tienen la libertad de variar. Cuanto más bajo sea el número de grados de libertad, más alto debe ser el valor t para obtener significación estadística.
Encontramos el número de grados de libertad:
- sumando los tamaños de muestra (número de mediciones) en ambas condiciones, luego
- restar 2.
Por tanto, el número de grados de libertad es 16 – 2 = 14
Paso 5: Verificar el valor crítico y compararlo con el valor t obtenido
Utilizando el valor obtenido para los grados de libertad, podemos leer el «valor crítico» de las cifras estándar que se muestran en la siguiente tabla.
Si el valor t es mayor que el valor crítico, existe una diferencia estadísticamente significativa entre los resultados en las dos condiciones. Esto significa que hay una probabilidad de no más del 5% (p ≤ 0,05) de que la diferencia haya ocurrido por casualidad.
| Grados de libertad | Valor crítico de significación (p ≤ 0,05) |
|---|---|
| 1 | 12.71 |
| 2 | 4.30 |
| 3 | 3.18 |
| 4 | 2.78 |
| 5 | 2.57 |
| 6 | 2.45 |
| 7 | 2.36 |
| 8 | 2.31 |
| 9 | 2.26 |
| 10 | 2.23 |
| 11 | 2.20 |
| 12 | 2.18 |
| 13 | 2.16 |
| 14 | 2.14 |
| 15 | 2.13 |
Para t = 2,94 el valor crítico es 2,14, por lo que el valor t excede el valor crítico. Esto significa que podemos rechazar la hipótesis nula, ya que es abrumadoramente probable que la diferencia en los resultados no haya ocurrido por casualidad.
Conclusión y discusión
En esta investigación, el valor de t ha sido mayor que el valor crítico en el grado de libertad relevante, por lo que rechazamos la hipótesis nula. Por lo tanto, podemos concluir que existe una diferencia estadísticamente significativa en el tamaño de las hojas que crecen en el suelo enriquecido en comparación con el suelo normal.
Además de discutir la conclusión estadística, a los estudiantes les puede gustar criticar el experimento en general y sugerir cualquier factor que pudiera haber afectado los resultados. ¿Pueden proponer alguna mejora?
Además, ¿existen otros conjuntos de datos que pueden ser interesantes de recopilar y analizar mediante la prueba t?
¿Qué hemos aprendido del proyecto?
Para los estudiantes de Secundaria, a los que les gusta ver crecer las plantas y salir del aula al invernadero, esta actividad les gusta y los motiva. En el próximo año académico, cultivaremos plantas que atraigan más a los gustos de los estudiantes, como tomates y guisantes, en lugar de rábanos.
Para los estudiantes de Bachillerato, hemos comprobado que estas actividades les han ayudado a desarrollar sus habilidades estadísticas, así como a obtener una mejor comprensión de la prueba de hipótesis, que es una parte esencial de cualquier trabajo práctico en biología. ¡Nuestros estudiantes ahora comprenden realmente lo que significa «significación estadística»!
Definitions
| Valor de p | El valor p es un número entre 0 y 1 que determina la significancia estadística de sus resultados. Un valor p pequeño (generalmente ≤ 0,05) indica una fuerte evidencia en contra de la hipótesis nula, por lo que rechaza la hipótesis nula. |
| Grados de libertad | Los grados de libertad en un cálculo estadístico representan cuántos valores involucrados en dicho cálculo tienen la libertad de variar. Este es un factor importante para saber si los resultados son estadísticamente significativos. |
| Desviación estándar | La desviación estándar es una medida que se utiliza para cuantificar la cantidad de variación en un conjunto de valores de datos. Una desviación estándar baja indica que los puntos de datos están cerca de la media del conjunto de datos, mientras que una desviación estándar alta indica que los puntos de datos están distribuidos en un rango más amplio de valores. |
| Hipótesis nula, Ho | Una hipótesis nula expresa la idea de que cualquier diferencia entre conjuntos de datos se debe al azar. |
| Significación estadística | En biología, un resultado es estadísticamente significativo si la probabilidad de que la hipótesis nula sea correcta es del 5% o menor (p ≤ 0,05). Entonces, un resultado estadísticamente significativo significa que estamos 95% seguros de que H0 no es correcta. |
Resources
- Puede obtener más información sobre prueba t y sus aplicaciones en biología en el sitio web Biology for Life.
- Descargue este recurso del consejo de exámenes escolares OCR sobre las diferentes pruebas estadísticas y cómo decidir cuál seleccionar.
- Obtenga más información sobre los grados de libertad en el sitio web Statistics by Jim.
Review
Este artículo muestra cómo las clases de biología de Secundaria y Bachillerato pueden cooperar para comprobar una hipótesis a través de la experimentación. Las clases de Secundaria hacen un experimento de cultivo de plantas al aire libre, lo que genera datos que son utilizados por las clases de Bachillerato para analizarlos con métodos estadísticos.
Si bien la actividad de cultivar plantas y medir su crecimiento no es especialmente nueva, combinar esto con un ejercicio de estadística proporciona una forma útil de enseñar la interpretación de datos en biología y la importancia de una evaluación estadística correcta en la ciencia.
Las actividades también brindan la oportunidad de aumentar la cooperación entre clases. Los estudiantes de Bachillerato año podrían considerar cómo mejorar el experimento para obtener mejores datos, por ejemplo, qué variable del experimento de crecimiento de las plantas sería más adecuada para medir y por qué, y luego compartir sus ideas con los estudiantes de Secundaria.
Monica Menesini, profesora de Ciencias, Italia





