Fai crescere i tuoi dati statistici Teach article
I tuoi studenti preferirebbero coltivare colture commestibili o darsi da fare con la statistica? Ecco un modo per combinare le due attività in un’applicazione dell’analisi statistica al mondo reale.
La maggor parte degli student di biologia preferiscono evitare la matematica, motivo per cui spesso scelgono biologia. Così nelle classi senior (età 16-18), quando vengono citati i test statistici, la classe intera sospira e molto spesso lo fa anche l’insegnante.

sempre è l’aspetto che più
interessa gli studenti
Sean/Flickr CC BY-ND 2.0
Nel 2018 abbiamo portato avanti un project work nella nostra scuola in Kazakhstan, coltivando piante nella serra scolastica con alcune delle classi di student più giovani. Nello stesso tempo, gli student più grandi di biologia stavano studiando il t-test, che è un modo standard per valutare un’ipotesi sperimentale. Introdurre la matematica nelle lezioni di scienze non è facile, così stabilimmo che sarebbe stato più eccitante usare i dati raccolti nel Progetto di crescita delle piante in modo da avere dati che si riferissero alla vita reale.
Il t-test è uno dei test statistici standard utilizzati per stabilire se c’è una differenza statistica significativa tra due insiemi correlati di dati – cioè se una differenza di questo tipo può essere capitata per caso. Far crescere piante in due condizioni diverse – terreno normale o fertilizzato- potrebbe fornire un’ipotesi da testare e due buoni insiemi di dati per un’analisi statistica.
L’idea si è rivelata un successo: abbiamo provato che utilizzando dati raccolti durante un esperimento che si sta realizzando a scuola fa sembrare l’analisi statistica più reale, e gli student possono vedere come il t-test ci renda capaci di trarre conclusion nella vita di tutti I giorni, piuttosto che essere soltanto un mero esercizio sulla carta.
In questo articolo descriviamo entrambi gli aspetti di questa attività: il progetto della serra e la conseguente analisi statistica usando il t-test. L’attività sulla serra è adata per studenti con 14-16 anni e richiede circa 8 ore di attività durante le lezioni, più 10-12 settimane per la crescita delle piante. L’attività del t-test è adatta per student di 16-18 anni e richiede circa 4 ore.
Per alcune definizioni di termini statistici si può utilizzare la casella di testo (o utilizzare risorse standard).

Joanne Brown
Fase 1: Coltiviamo piante nella serra

appezzamenti arricchiti (in
alto) sono di colore più chiaro
rispetto a quelli normali (in
basso).
Joanne Brown
Alla maggior parte degli studenti piace veder crescere le piante, pertanto vale comunque la pena di fare un esperimento di orticoltura. Il Kazakhastan ha un clima continentale, con estate molto calde ed inverni estremamente freddi, per questo motive per coltivare piante in primavera abbiamo utilizzato una serra riscaldata. Naturalmente le piante possono essere cultivate all’esterno se la stagione e le condizioni climatiche lo consentono.
Una cosa importante: scegliere un’ipotesi chiara e due differenti condizioni di crescita per testare l’ipotesi. Noi abbiamo scelto le seguenti:
Scopo dell’esperimento: stabilire se arricchendo il terreno con dei nutrienti le foglie di ravanello crescono di più.
Ipotesi: Le piante di ravanello che crescono su un terreno arricchito di nutrient avranno foglie più grandi.
Per arricchire il terreno, abbiamo aggiunto letame di fattoria contenente potassio (1,3%), azoto (0,1%) e magnesio (0,6%).
Materiali
- Semi di ravanello (circa 160 in totale o 10 semi per appezzamento)
- Area di terreno normale per la semina, almeno 16 m2
- Letame da cortile (4 kg in totale o 500 g per appezzamento)
- Picchetti
- Annaffiatoio
- Metro a nastro
- Righello
- Calcolatrice
Procedura
Gli studenti possono seguire tutti i passaggi necessari per far crescere le piante.
Avvertenza di sicurezza:
lavarsi sempre le mani dopo aver toccat il terreno o il concime.
- Per preparare il terreno, utilizzare la vanga per scavare e capovolgerlo fino a dividerlo abbastanza finemente.
- 2Misurare 16 lotti di 1 m2 ciascuno utilizzando il metro a nastro: otto per il terreno arricchito e otto per il terreno normale. Segnare le trame usando una corda, quindi etichettare ogni lotto con il suo numero.
- Aggiungere 500 g di letame da cortile a ciascuno degli otto lotti arricchiti. Usare le vanghe per mescolarlo bene con il terreno.
- Piantare dieci semi di ravanello in ciascun lotto, a circa 100 mm di distanza e a 10 mm di profondità.
- Innaffiare le piante ogni giorno o secondo necessità. Osservare la crescita delle piante per circa sette settimane, dalla germinazione alle piantine e poi alle piante completamente sviluppate.
- Un giorno alla settimana (ad esempio il venerdì) durante il periodo di crescita, usare un righello per misurare la lunghezza della foglia più grande di ciascuna pianta in tutti i 16 lotti. Registrare attentamente queste misurazioni.
Al termine del periodo di crescita, calcolare la lunghezza media di queste foglie in ogni lotto su tutto il period di crescita. Questa viene calcolata sommando tutte le misure per il singolo lotto e poi dividend il risultato per il numero di misurazioni.

Joanne Brown
Risultati e conclusioni
Nel nostro esperimento sono cresciute 67 piante di ravanello nei lotti con il terreno arricchito e 99 piante nel terreno normale (i numeri differivano tra di loro perchè era difficile contare con precisione i semi, inoltre alcuni non erano germogliati.
La tabella qui sotto mostra le lunghezze medie delle foglie più grandi delle piante in ciascun lotto durante il period di crescita e la media risultante in ogni condizione.
| Terreno arricchito: numeri dei lotti | Lunghezza media delle foglie più grandi in ogni lotto (mm) | Terreno normale: numeri dei lotti | Lunghezza media delle foglie più grandi in ogni lotto (mm) | |
|---|---|---|---|---|
| 1 | 39 | 9 | 38 | |
| 2 | 45 | 10 | 41 | |
| 3 | 41 | 11 | 43 | |
| 4 | 46 | 12 | 39 | |
| 5 | 45 | 13 | 37 | |
| 6 | 48 | 14 | 38 | |
| 7 | 39 | 15 | 41 | |
| 8 | 44 | 16 | 36 | |
| Media complessiva (terreno arricchito) | 43.38 | Media complessiva (terreno normale) | 39.13 |
Come dimostrano questi risultati, le foglie erano in media davvero più grandi nei lotti cui erano stati aggiunti dei nutrient, in linea con le nostre ipotesi.
Per una classe junior è adeguato concludere che questi risultati concordano con l’ipotesi. Tuttavia, ad un livello scolastico senior (e nelle scienze reali), dovremmo dimostrare che questi risultati non sis ono ottenuti per casi – in alter parole, che è statisticamente significativo. Questo è lo scopo della fase successiva dell’attività.
Fase 2: Utilizzo del t-test
I risultati dell’esperimento di orticoltura possono essere utilizzati come dati ‘reali’ da analizzare usando il t-test per student di livello più avanzato.
Il t-test viene usato per stabilire se c’è una differenza statisticamente significative (cioè non casuale) tra le medie dei due insiemi di dati e quindi tra due condizioni sperimentali diverse. In questo caso gli student indagano se arricchire il terreno ha fatto una differenza statisticamente significativa sulle dimensioni delle foglie di ravanello, rispetto ad un terreno normale, oppure se la differenza tra le dimensioni delle foglie è avvenuta per caso.
Procedura
Per utilizzare il t-test abbiamo bisogno di due insiemi di dati dall’esperimento di crescita delle piantine (suolo normale e arricchito). Successivamente va seguito un procedimento matematico standard per analizzare i dati e trovare se convalidano l’ipotesi scelta.
Passaggio 1: Stabilire l’ipotesi nulla H0
Per stabilire utilizzando il t-test se un’ipotesi è supportata dai dati, dobbiamo prima decidere un’’ipotesi nulla’. In generale, questa è l’ipotesi per cui le diverse condizioni non influiscano sui risultati. Quindi, se l’analisi dei dati mostra che possiamo rifiutare questa ipotesi, allora possiamo concludere che le diverse condizioni hanno fatto la differenza per i risultati.
Qui l’ipotesi nulla H0 è
Non ci sarà differenza significative nelle dimensioni medie delle foglie di ravanello che crescono su un terreno arricchito piuttosto che su uno normale.
Passaggio 2: Calcolare la deviazione standard in ogni condizione
Di seguito calcoliamo la deviazione standard (SD) per ciascuno dei due insiemi di dati
Deviazione standard (SD) =
Dove:
x = valore medio per ogni lotto di terreno (vedi tabella 1)
x̅ = media delle medie di tutte le misure in una condizione (terreno arricchito, terreno normale); vedi tabella 1
n = numero di misurazioni in ogni condizione (8 in questo caso)
Per esempio nel lotto 1:
x = 39
x̅ = 43.38
Quindi (x – x̅)2 = (39 – 43.38)2 = 19.18
I risultati completi sono riportati nella tabella 2.
| Numero del lotto | Terreno arricchito, dimensioni delle foglie (mm) | (x – x̅)2
x̅ = 43.38 |
Numero del lotto | Terreno normale, dimensioni delle foglie (mm) | (x – x̅)2
x̅ = 39.13 |
|
|---|---|---|---|---|---|---|
| 1 | 39 | 19.18 | 9 | 38 | 1.28 | |
| 2 | 45 | 2.62 | 10 | 41 | 3.50 | |
| 3 | 41 | 5.66 | 11 | 43 | 14.98 | |
| 4 | 46 | 6.86 | 12 | 39 | 0.02 | |
| 5 | 45 | 2.62 | 13 | 37 | 4.53 | |
| 6 | 48 | 21.34 | 14 | 38 | 1.28 | |
| 7 | 39 | 19.18 | 15 | 41 | 3.50 | |
| 8 | 44 | 0.38 | 16 | 36 | 9.80 | |
| Total | 77.84 | Total | 38.89 |
Quindi la deviazione standard per il terreno arricchito (SD1)
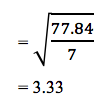
La deviazione standard per il terreno normale (SD2):
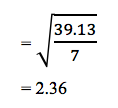
Passaggio 3: Calcolare il valore t complessivo
Possiamo calcolare il valore t usando l’equazione seguente
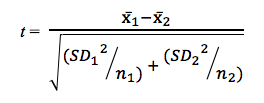
Dove:
x̅1= media dei risultati nella prima condizione (terreno arricchito)
x̅2 = media dei risultati nella seconda condizione (terreno normale)
n1 = numero delle misurazioni nella prima condizione
n2 = numero delle misurazioni nella seconda condizione
Quindi:
x̅1 – x̅2 = 43.48 – 39.13
= 4.25
SD12= 3.332 = 11.09
SD22 = 2.362 = 5.57
n1 = n2 = 8
11.09/8 = 1.39
5.57/8 = 0.70
Quindi:
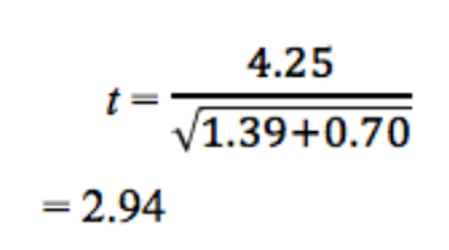
Nel prossimo passaggio utilizzeremo questo valore t per dimostrare se i dati supportano l’ipotesi nulla o se dobbiamo rigettarla.
Passaggio 4: Trovare I ‘gradi di libertà’
I ‘gradi di libertà’ in un calcolo statistico rappresentano un concetto matematico che indica quanti valori coinvolti nel calcolo sono liberi di variare. Minori sono i gradi di libertà, più alto deve essere il valore t perchè ci sia una significatività statistica.
Possiamo trovare i gradi di libertà
- sommando le dimensioni del campione (numero delle misurazioni) in entrambe le condizioni, quindi
- sottraendo 2.
Così in questo caso il valore dei gradi di libertà è 16 – 2 = 14
Passaggio 5: Controllare il valore critico e confrontarlo con il valore t ottenuto
Utilizzando il valore calcolato per i gradi di libertà, possiamo leggere il valore critico dalle cifre significative riportate nella tabella sottostante.
Se il valore t è maggiore del valore critic, c’è una differenza satistica significative tra I risultati nelle due condizioni. Questo significa che c’è una probabilità di non più del 5% (con p ≤ 0.05) che la differenza sia dovuta al caso.
| Gradi di libertà | Valore critico per la significatività (con p ≤ 0.05) |
|---|---|
| 1 | 12.71 |
| 2 | 4.30 |
| 3 | 3.18 |
| 4 | 2.78 |
| 5 | 2.57 |
| 6 | 2.45 |
| 7 | 2.36 |
| 8 | 2.31 |
| 9 | 2.26 |
| 10 | 2.23 |
| 11 | 2.20 |
| 12 | 2.18 |
| 13 | 2.16 |
| 14 | 2.14 |
| 15 | 2.13 |
Qui t = 2.94 e il valore critico è 2.14, quindi il valore t supera il valore critico. Ciò significa che possiamo rifiutare l’ipotesi nulla, poiché è estremamente probabile che la differenza nei risultati non sia avvenuta per caso.
Conclusione e discussione
In questo studio il valore di t era maggiore del valore critico al relative grado di libertà, quindi possiamo rifiutare l’ipotesi nulla. Pertanto, possiamo concludere che esiste una differenza statisticamente significativa nella dimensione delle foglie che crescono nel terreno arricchito rispetto al terreno normale.
Oltre a discutere la conclusione statistica, gli studenti potrebbero voler criticare l’esperimento complessivo e suggerire eventuali fattori che potrebbero aver influenzato i risultati. Hanno miglioramenti da proporre?
Inoltre, ci sono altri insiemi di dati che potrebbero essere interessanti da raccogliere e analizzare utilizzando il test t?
Cosa abbiamo imparato dal Progetto?
Per gli studenti più giovani, a cui piace vedere crescere le piante, uscire dall’aula per recarsi nella serra durante la lezione li incoraggia. Nel prossimo anno accademico, coltiveremo piante che soddisfano maggiormente i gusti degli studenti, come pomodori e piselli dolci, piuttosto che ravanelli.
Per gli studenti senior, abbiamo scoperto che queste attività li hanno aiutati a sviluppare le loro abilità statistiche, nonché ad acquisire una migliore comprensione della verifica delle ipotesi, che è una parte essenziale di qualsiasi lavoro pratico in biologia. I nostri studenti ora capiscono cosa significa effettivamente “significatività statistica”!
Definizioni
| p-value | Il p-value è un numero tra 0 e 1 che determina la significatività statistica dei tuoi risultati. Un p-value piccolo (di solito ≤ 0.05) indica una forte evidenza contro l’ipotesi nulla, così che essa viene respinta. |
| Gradi di libertä | I gradi di libertà in un calcolo statistico indicano quanti valori coinvolti nel calcolo possono variare. Rappresentano un fattore importante per determinare se I risultati sono statisticamente significative. |
| Deviazione standard | La deviazione standard è una misura utilizzata per quantificare la variazione in un insieme di valori di dati. Una deviazione standard bassa indica che i punti dati sono vicini alla media dell’insieme di dati, mentre una deviazione standard alta indica che i punti dati sono distribuiti su una gamma più ampia di valori. |
| Ipotesi nulla H0 | Un’ipotesi nulla esprime l’idea che qualsiasi differenza tra insiemi di dati sia dovuta al caso. |
| Significatività statistica | In biologia, un risultato è statisticamente significativo se la probabilità che l’ipotesi nulla sia corretta è del 5% o inferiore (p ≤ 0,05). Quindi un risultato statisticamente significativo indica che siamo sicuri al 95% che H0 non è corretto. |
Resources
- Si possono reperire più informazioni sul t-test e le sue applicazioni in biologia sul sito di Biology for Life.
- È possible effettuare il download di questa risorsa dal board d’esame OCR sui diversi test statistici e su come decider quale utilizzare.
- Si possono avere informazioni aggiuntive sui gradi di libertà dal sito Statistics by Jim.
Review
Questo articolo mostra come le classi di biologia junior e senior possono cooperare per testare un’ipotesi attraverso la sperimentazione. Le classi junior fanno un esperimento coltivando piante all’aperto, che genera dati che vengono utilizzati dalle classi senior per analizzare con metodi statistici.
Sebbene l’attività di coltivazione delle piante e di misurazione della loro crescita non sia particolarmente nuova, associarla a un esercizio di statistica fornisce un modo utile per insegnare l’interpretazione dei dati in biologia – e l’importanza di una corretta valutazione statistica nelle scienze.
Le attività forniscono anche un’opportunità per aumentare la cooperazione tra le classi. Gli studenti senior potrebbero valutare come migliorare l’esperimento per ottenere dati migliori – ad esempio, quale variabile nell’esperimento di crescita delle piante sarebbe più adatta da misurare e perché – e quindi condividere le loro idee con gli studenti junior.
Monica Menesini, docente di scienze, Italia





