Modelizado del Cambio Climático en el aula Teach article
Traducido por Javier Aseguinolaza. ¿Por qué no hacer que tus estudiantes hagan sus propias predicciones de cambio climático – con la ayuda de Dudley Shallcross y Tim Harrison de la Universidad de Bristol, Reino Unido?
El Cambio Climático y el calentamiento global son temas “calientes” y merecen un espacio importante en el plan de estudios de ciencias de la escuela. BPero, ¿cómo predecimos cómo va a cambiar nuestro clima? Parece oportuno introducir a los estudiantes en el modelizado simple del clima. En este artículo, demostramos que los estudiantes pueden utilizar hojas de cálculo sencillas para investigar los factores clave que afectan al clima de la Tierra.
Un primer intento de modelizar el clima
El modelo más simple del clima es en el que la energía solar incidente es igual a la energía emitida por el planeta, esto es, un modelo en que “la energía entrante es igual a la saliente”. En este artículo, el término “energía” significa realmente flujo de energía, esto es, energía por segundo. Sabemos, a partir de las mediciones, que la energía del Sol, que alcanza la parte alta de la atmósfera (por segundo), denominada constante solar S, es 1370 Wm-2.
Comenzamos calculando la temperature media de la superficie de la Tierra, TE. Si tomamos el radio RE de una Tierra perfectamente esférica, en este simple modelo podemos ver que la Tierra absorbe la radiación solar en un área de πRE2(esto es, disco plano de atmósfera) pero emite energía desde un área 4πRE2(esto es, desde la superficie completa).
(a) Energía entrante = energía saliente
Y utilizando la Ley de Stefan-Boltzmann (ver caja)
(b) La energía por unidad de area por unidad de tiempo x area total(disc) = energía por unidad de área por unidad de tiempo x área total(sphere)
(c) 1370 x πRE2 = σTE4 x 4πRE2
Reorganizando la ecuación da:
σTE4 = 1370 = S/4
4
TE4 = 1370
(4 x 5.67 x 10-8)
TE = 279 K (6 °C)
donde σ es la constante de Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
A primera vista, esto parece una figura demasiado sensible para un modelo crudo, aunque por supuesto la temperatura media real de la Tierra e se sabe que son 16 °C. (Hay varias formas de solucionarlo, tales como separar la tierra en bandas de latitud, obteniendo las temperaturas medias por cada banda y sumando y promediando todas ellas). El problema de este simple modelo, sin embargo, es que hay una parte de la energía solar que no la absorbe la Tierra, sino que es reflejada de vuelta al espacio por las nubes y el hielo.
Aproximadamente el 24% de la energía entrante es reflejada por las nubes y otro 6% es reflejada por la superficie, esto es, por el hielo. Esto da una reflectividad total de la Tierra – conocida como albedo (A) – de un 30% o 0.3. Por lo tanto, la parte izquierda de la ecuación (c) debe ser reescrita ahora como 0.7 x 1370 x πRE2y el cálculo de la TE es:
TE4 = 1370 x 0.7
(4 x 5.67 x 10-8)
TE = 255 K (-18 °C)
Este valor es obviamente muy bajo, y lleva naturalmente a la cuestión: ¿Por qué es la Tierra tan templada? Con el objeto de responder esta pregunta necesitamos un modelo ligeramente más complejo.
Antecedentes esenciales físicos
La radiación del cuerpo negro y la Ley de Stefan-Boltzman
Todos los cuerpos radian energía en forma de radiación electromagnética. Un cuerpo negro absorbe toda la radiación que incide en él. Emite radiación en función de la temperatura de su superficie.
La Ley de Stefan-Boltzmann describe la energía total, I, emitida por un cuerpo negro a cualquier temperature, T, como:
I(T) = σT4 (Ecuación 1)
donde:
I es la energía por unidad de área emitida por segundo (Wm-2)
T es la temperature absoluta (K)
σ es la constante de Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
Black body radiation and the Stefan-Boltzmann Law
El modelo de Tierra de una sola capa atmosférica
Si suponemos que la atmósfera está compuesta de una sola capa de gases miscibles, podemos crear un modelo más preciso que los estudiantes puedan utilizar en una hoja de cálculo. En este modelo, se hacen suposiciones sobre la absorción atmosférica de la luz visible entrante del sol y sobre la absorción de la luz infrarroja emitida por la Tierra.
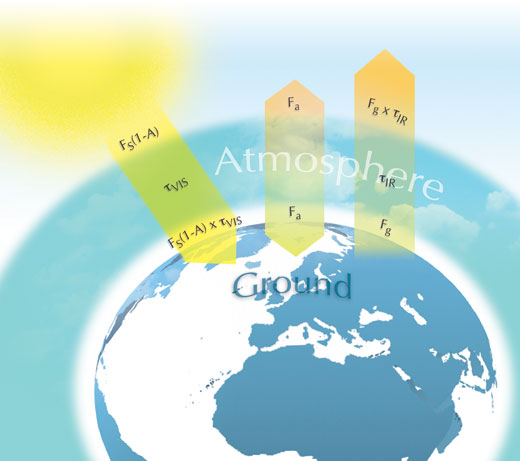
La figura de Abajo resume los elementos del modelo. FS es la constante solar dividida por 4 (S/4), que surge de la diferencia entre la energía entrante repartida sobre un disco, πr2, y la energía saliente radiada desde la superficie de una esfera, 4πr2 (la suposición realizada en el primer modelo). La energía entrante del sol es entonces FS(1-A), donde A es el albedo – la porción reflejada de vuelta al espacio. Esta energía entrante se encuentra en registros de regiones visibles y UV. τVIS es la proporción de esta energía entrante que no es absorbida por la atmósfera: si la atmósfera la absorbe toda, τVIS es cero; si la atmósfera no absorbe nada, τVIS es uno. Por lo tanto, la energía que alcanza la superficie del planeta es FS(1-A) x τVIS.
La Tierra se comportará de forma similar a un cuerpo negro y emitirá la enegía notada como Fg desde su superficie. Esta radiación terrestre está centrada en la región infrarroja del espectro. Ciertos gases de la atmósfera absorben la energía infrarroja (gases de efecto invernadero). De forma similar a τVIS, τIR es la proporción de energía infrarroja no absorbida por estos gases de la atmósfera, por lo que la energía salientes es Fg x τIR.
Suponiendo que la energía de la atmósfera es Fa y que la energía entrante y saliente de la superficie de la tierra y la parte alta de la atmósfera, están ambas equilibradas, entonces:
En la superficie de la Tierra:
FS(1-A) x τVIS + Fa = Fg (Ecuación 2)
y en la parte alta de la atmósfera:
Fg x τIR + Fa = FS(1-A) (Ecuación 3)
Combinando las Ecuaciones 2 y 3 da:
Fg = FS(1-A)(1 + τVIS)
(1 + τIR)
Finalmente,
Fg = σTE4 = FS(1-A)(1 + τVIS)
(1 + tIR)
TE = [ FS(1-A)(1 + τVIS) ]0.25
[ σ(1 + τIR) ] (Ecuación 4)
Si tomamos los siguientes valores:
FS = 1370/4 = 342.5 Wm-2 (constante solar dividida por 4)
A = 0.3
τVIS = 0.8
τIR = 0.1
La ecuación 4 nos das:
TE = 288.5 K (15.5 °C),
Lo cual es una aproximación cercana a la media real de la temperature en la superficie de la Tierra.
Es la ecuación 4 la que puede ser introducida en un programa como Microsoft Excel para que los estudiantes puedan ver los cambios en la temperature global cuando se cambian los parámetros de la ecuación. Esto se ha hecho y hay una versión interactiva que puede utilizarse online o bajada desde el websitew1 de la Universidad de Bristol.
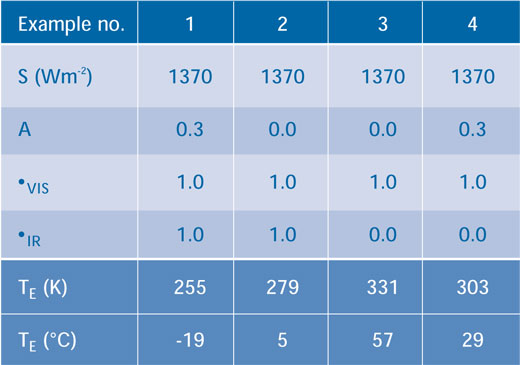
La Tabla 1 muestra ejemplos de los resultados si las variables A, τVIS y τIR se modifican. En el Ejemplo 1 suponemos que la atmósfera no absorbe nada de los flujos de energía entrants o salientes (esto es, ambos τVIS y τIRson iguales a 1.0) y el albedo es 0.3, dando una temperatura def 255 K. En el Ejemplo 2, suponemos que no hay nubes ni hielo (esto es, A = 0.0), lo que eleva la temperatura d ela Tierra a 279 K, mostrando la importancia del albedo. En el Ejemplo 3, tampoco hay nubes o hielo (A = 0.0) pero ahora la atmósfera absorbe toda la radiación infrarroja saliente (esto es τIR = 0.0) y la Tierra se calienta hasta los 331 K. Si ahora reintroducimos nubes y hielo en el Ejemplo 4 (A = 0.3), la temperatura cae a los 303 K.
Preguntas posibles
Las preguntas típicas que pueden hacerse, y que requerirían que los estudiantes usaran este modelo, son:
- ¿Cuál de las variables tiene el mayor efecto en la temperature media global?
- Si la distancia media de la Tierra al Sol se incrementara un 1% sobre el valor actual, la constante solar se reduciría por un factor de 1.0201, estoe s, sería 1343 Wm-2. ¿Cuál sería la temperatura? Suponga un albedo de 0.3, τIR de 0.3 y τVIS de 0.6.
(La constante solar se escalaría con el cuadrado d ela distancia, luego mover la Tierra un 10% más cerca del Sol significará S = 1370/(0.9)2 = 1691 Wm-2 y mover la Tierra un 1% más allá significará S = 1370/(1.01)2 = 1343 Wm-2)
Por supuesto, se pueden realizar preguntas más desafiantes.
- Si la arena del desierto del Sáhara pudiera convertirse en un espejo de cristal (la arena se puede fundir para dar cristal/vidrio),
- Cómo d egrande debería ser el Espejo para conseguir enfriar el planeta 1 °C?
- Qué fracción de desierto del Sáhara sería?
Un modelo más sofisticado
¿Cómo es el modelo simple en comparación con modelos más sofisticados tales como el modelo de clima del Hadley Centre usado por la Oficina Meteorológica del reino Unido (ver imágenes abajo)? De hecho, los dos modelos son muy similares, excepto que el modelo del Hadley Centre no tiene en cuenta la atmósfera como una sola capa, sino que la descompone en una serie de cajas en base a la altitud, latitud y longitud. Para cada caja, el modelo calcula directamente la cantidad de radiación UV/visible entrante transmitida y dispersada en esa caja, y la cantidad de radiación infrarroja saliente transmitida por dicha caja, en base a las concentraciones de gases clave de efecto invernadero y del área de la superficie de nubes y hielo. Las versiones más sofisticadas del modelo del Hadley Centre también tienen en cuenta el flujo de calor que entra y sale de los océanos así como del consumo de CO2 que realiza la vegetación. Pero si entiende los principios del modelo simple, está en el buen camino para comprender los modelos climáticos reales más complicados.
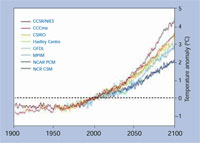
global; Predicciones del modelo
climático para el calentamiento
global en relación a la temperatura
media global de 2000. Los datos
del modelo utilizados fueron
tomados del Centro de Distribución
de datos del Panel
Intergubernamental para el Cambio
Climático. Haga clic sobre la imagen
para ampliarla
Imagen cortesía de Robert A. Rohde
; Fuente de la imagen: Wikimedia Commons
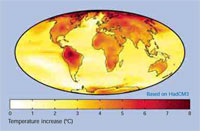
global; predicción 2070-2100 vs.
media 1960-1990 Un mapa del
calentamiento global previsto a
final del siglo XXI. Este modelo
tiene un calentamiento global de
3.0°C y utiliza el modelo climático
Hadley Centre HadCM. Haga clic
sobre la imagen para ampliarla
Imagen cortesía de Robert A. Rohde;
Fuente de la imagen: Wikimedia Commons
Tomar parte en una simulación real de clima
Climateprediction.netw2 es el mayor experimento para intentar producir una predicción del clima para el siglo 21. Lo hace recogiendo ayuda de personas alrededor del mundo que pueden ofrecer tiempo de sus ordenadores – tal como el encendido del ordenador, en el que no se utilice en su total capacidad. El modelo climático completo tiene muchos parámetros que pueden ser ajustados; para explorar todos estos parámetros, se tiene que realizar una cantidad ingente de simulaciones. Incluso con los recursos informáticos disponibles para el climateprediction.net team, el ensamblaje de tales simulaciones llevaría un largo tiempo. La idea detrás de climateprediction.net es que cualquiera pueda bajarse una versión del modelo para explorar en cada uno de estos parámetros (preestablecidos). El modelo tarda unos tres meses en funcionar en el fondo mientras usted trabaja, sin comprometer la velocidad del ordenador.
Los cálculos se realizan en tres partes. La primera parte realiza cálculos utilizando datos de los años 1850 a 1900, verificando las predicciones resultantes frente a registros de temperatura: esto se conoce como la calibración. La segunda parte realiza una simulación desde 1901 hasta el presente. El tercer paso realiza una simulación del clima futuro (2000-2100) cambiando un parámetro, por ejemplo la sensibilidad del clima frente a las incertidumbres del ciclo del azufre. Una vez que se han completado los cálculos, los datos se suben automáticamente a la Oficina Meteorológica del Reino Unido la siguiente vez en que el ordenador está online. El software de interfaz provisto (libre de cargas) con la simulación da al usuario del ordenador un gráfico con los cambios del clima, según se calculan. Variaciones de temperatura por estación con la latitude, longitude y altitude son una parte de las variables que se pueden visualizar. Tales funcionalidades permitirían desarrollar un proyecto de escuela con plan de estudios transversal uniendo geografía y ciencias físicas.
En el próximo ejemplar de Science in School, los autores proponen algunos experimentos químicos relevantes para el cambio climático.
Web References
- w1 – Una version interactiva del modelo simple de clima se puede utilizar online o descargar aquí: www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- Use las fichas para cambiar las variables.
- w2 – Para más detalles sobre el experimento y cómo involucrarse, ver http://climateprediction.net.
- La web de climateprediction.net ofrece también información y recursos especialmente para los colegios, disponibles tanto en inglés como en español: http://climateprediction.net/content/resources-schools
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- En el siguiente enlace se pueden localizar numerosos apuntes para profesores de contaminación del aire, cambio climático y el agotamiento de la capa de ozono: www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html
- Para una Fuente excelente de gráficos y datos relacionados con cambio climático, ver: www.grida.no/climate/vital/index.htm
- Datos del Earth System Research Laboratory Global Monitoring Station: www.cmdl.noaa.gov
- La web del Intergovernmental Panel on Climate Change (IPCC), en el que se puede localizar el informe de cambio climático de 2007 y otros datos: www.ipcc.ch
- Haubold B (2008) Una verdad incómoda. Science in School 9. www.scienceinschool.org/2008/issue9/inconvenient/spanish
Review
El cambio climático debería ser ciertamente uno de los temas de la enseñanza actual en todos los niveles de la enseñanza a lo largo de Europa. En particular tras la gran campaña de Al Gore Una Verdad Inconveniente (Inconvenient Truth) , el tema ha ganado un reconocimiento de escala mundial. Sin embargo, no siempre hay disponible material útil con información de fondo o precedente utilizable para los profesores de ciencia. Este artículo, sin embargo, ofrece una aproximación adecuada y fácilmente adaptativa al complicado proceso de modelizado de los desarrollos atmosféricos.
Mientras el modelo matemático es más adecuado para su uso en cursos avanzados de ciencia para estudiantes de 16 años en adelante, el fenómeno básico se puede presentar fácilmente a estudiantes de 15 años e incluso menores – tanto si no tienen intención de especializarse en ciencia en los siguientes años. Los recursos web mencionados ofrecen un amplio rango de aproximaciones, imágenes y gráficos preparadas para ser utilizadas, proporcionando así un recurso muy útil para cualquier profesor de ciencia.
Tobias Kirschbaum, Alemania





