Modélisation du changement climatique en classe Teach article
Traduit par Nathalie Bisson. Pourquoi ne pas amener vos élèves à créer leurs propres prévisions de changement climatique- avec l’aide de Dudley Shallcross et Tim Harrison de l’Université de Bristol, au Royaume Uni?
Le changement climatique et le réchauffement global sont des sujets “chauds” qui méritent une place importante dans le cursus scolaire scientifique. Mais comment peut-on prévoir les modalités de ce changement climatique? Il semble que c’est le bon moment pour initier les élèves à une modélisation climatique simple. Dans cet article nous montrons que les élèves peuvent utiliser une feuille de calcul informatique très simple, pour découvrir les principaux facteurs qui affectent le climat de la Terre.
Premier essai de modélisation du climat
Le modèle climatique le plus simple est celui dans lequel l’énergie solaire incidente égale l’énergie radiative terrestre émise vers l’espace, c’est-à-dire un modèle «d’équilibre entre l’énergie qui entre et celle qui sort». Dans cet article, le terme d’énergie recouvre vraiment le flux d’énergie, en unité d’énergie par seconde. Nous savons, grâce à des mesures, que l’énergie solaire atteignant le sommet de l’atmosphère (par seconde) est de 1370 Wm-2, c’est ce que l’on appelle la constante solaire S.
Commençons par calculer la température moyenne de surface de la Terre, TE. Si nous considérons que la Terre est une sphère parfaite de rayon RE, nous voyons que la Terre, dans ce modèle très simple, absorbe les radiations solaires par une surface égale à πRE2 (c’est-à-dire un disque plat d’atmosphère), alors qu’elle émet de l’énergie par une surface égale à 4πRE2 (c’est-à-dire par toute sa surface).
(a) on pose : énergie incidente = énergie radiative
Utilisons la loi de Stefan-Boltzmann (voir encadré)
(b) énergie par unité de surface et de temps X aire totale(disque) = énergie par unité de surface et de temps X aire totale(sphère)
(c) 1370 x πRE2 = σTE4 x 4πRE2
En réarrangeant ces équations, on obtient:
σTE4 = 1370 = S/4
4
TE4 = 1370
(4 x 5.67 x 10-8)
TE = 279 K (6 °C)
Où σ est la constante de Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
En première approche, ceci semble un résultat intéressant pour un modèle aussi simpliste, bien qu’on sache que la véritable température moyenne terrestre soit de 16°C. (Il y a plusieurs façons de s’en sortir, comme de diviser la Terre en bandes latitudinales, de calculer la température moyenne par bande, puis de faire la moyenne de toutes ces valeurs). En fait, le problème, avec ce modèle très simple, est qu’une partie de l’énergie solaire n’est pas absorbée mais est renvoyée vers l’espace par les nuages et la glace.
Environ 24% de l’énergie incidente est réfléchie par les nuages, et 6% supplémentaires par la surface et en particulier la glace. Ceci donne une réflectance totale de la Terre –connue sous le nom d’albédo terrestre (A)- de 30% ou 0,3. Par suite, le membre gauche de l’équation (c) doit maintenant être réécrit comme suit: 0,7 x 1370 x πRE2 et le calcul de TE devient:
TE4 = 1370 x 0.7
(4 x 5.67 x 10-8)
TE = 255 K (-18 °C)
Cette valeur est beaucoup trop basse, et conduit naturellement à la question : pourquoi la Terre est elle si chaude ? pour répondre à cette question, nous avons besoin d’un modèle un petit peu plus compliqué.
Quelques bases nécessaires de Physique
La loi de Stefan-Boltzmann et l’émission des corps noirs
Tous les corps émettent de l’énergie sous forme de radiations électromagnétiques. Un corps noir absorbe toutes les radiations qui l’atteignent. Il émet des radiations en relation avec sa température de surface. La loi de Stefan-Boltzmann décrit l’énergie totale, I, émise par un corps noir à une température T:
I(T) = σT4 (Équation 1)
where:
I est l’énergie émise par seconde et par unité de surface (Wm-2)
T est la température absolue (K)
σ est la constant de Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
Le modèle terrestre à une seule couche atmosphérique
Si on suppose que l’atmosphère est faite d’une seule épaisseur d’un mélange de gaz, nous pouvons créer un modèle plus pertinent que les étudiants peuvent manipuler avec leur programme. Dans ce modèle, l’absorption par l’atmosphère de la lumière incidente du soleil dans le domaine du visible, et l’absorption des radiations infrarouges émises par la terre sont prises en considération.
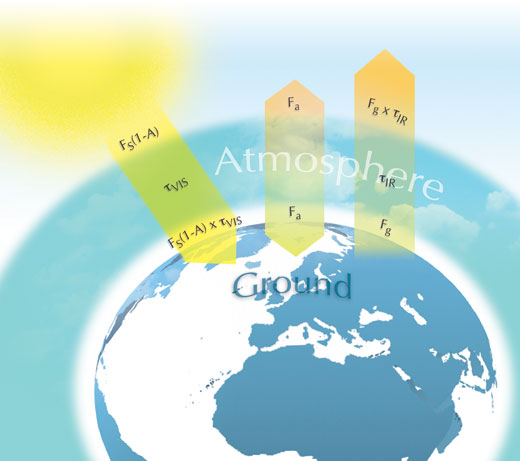
La figure ci-dessous résume les éléments de ce modèle. FS est la constante solaire divisée par 4 (S/4), qui est calculée comme la différence entre l’énergie incidente répartie sur un disque, πr2, et l’énergie émise par la surface d’une sphère, 4πr2 (hypothèse déjà formulée dans le premier modèle). L’énergie apportée par le soleil est alors FS (1-A), où A est l’albédo -la partie réfléchie vers l’espace. L’énergie incidente comprend des radiations ultra-violettes et visibles. τVIS est la partie de l’énergie incidente qui n’est pas absorbée par l’atmosphère : si l’atmosphère l’absorbe toute, τVIS est nul; Si l’atmosphère n’en absorbe pas du tout,est égal à 1. Par conséquent, l’énergie qui atteint la surface de la planète est donnée par FS(1-A) x τVIS.
La Terre se comporte comme un corps noir et émet l’énergie notée Fgà partir de sa surface. Cette émission radiative terrestre est centrée dans le domaine infrarouge du spectre. Certains gaz de l’atmosphère absorbent le rayonnement infrarouge (gaz à effet de serre). Parallèlement o τVIS, τIR est la proportion du rayonnement infrarouge qui n’est pas absorbée par les gaz à effet de serre. Par conséquent l’énergie émise par la Terre est Fg x τIR.
Si on pose que l’énergie venant de l’atmosphère est notée Fa et que l’énergie échangée par la surface terrestre et celle échangée au sommet de l’atmosphère se compensent, alors:
À la surface de la Terre:
FS(1-A) x τVIS + Fa = Fg (Équation 2)
Et au sommet de l’atmosphère:
Fg x τIR + Fa = FS(1-A) (Équation 3)
La combinaison des équations 2 et 3 donne:
Fg = FS(1-A)(1 + τVIS)
(1 + τIR)
Finalement,
Fg = σTE4 = FS(1-A)(1 + τVIS)
(1 + τIR)
TE = [ FS(1-A)(1 + τVIS) ]0.25
[ σ(1 + τIR) ] (Équation 4)
Faisons l’application numérique avec les valeurs suivantes :
FS = 1370/4 = 342.5 Wm-2 (constante solaire divisée par 4)
A = 0.3
τVIS = 0.8
τIR = 0.1
Alors l’équation 4 nous donne:
TE = 288.5 K (15.5 °C),
Cette valeur est une bonne approximation de la température moyenne de surface de la Terre couramment admise.
C’est l’équation 4 qui peut être insérée dans une feuille de calcul de Microsoft Excel par exemple, de façon à ce que les étudiants puissent voir les changements de la température globale lorsque les paramètres de l’équation changent. Ceci a été fait et une version interactive peut être utilisée en ligne ou téléchargée depuis le site internet de l’Université de Bristolw1.
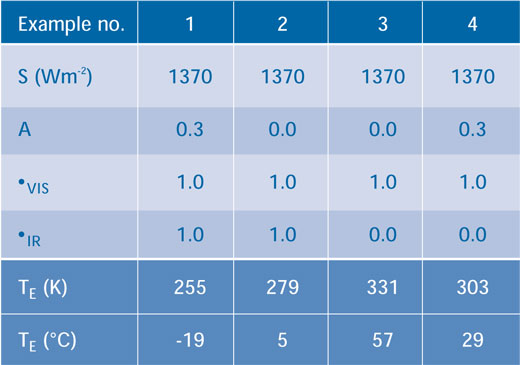
Le tableau 1 donne des exemples de résultats lorsque les variables, τVIS et τIR changent. Dans l’exemple 1, on fait l’hypothèse que l’atmosphère n’absorbe aucun des flux d’énergie entrant ou sortant (c’est-à-dire que τVIS et τIR sont égaux à 1) et que l’albédo est de 0,3, Ce qui donne un résultat de 255K. Dans l’exemple 2, on fait l’hypothèse qu’il n’y a ni nuages ni glace (c’est-à-dire que A = 0), ce qui élève la température de la Terre à 279K, montrant l’importance de l’albédo. Dans l’exemple 3, il n’y a pas non plus de nuages ou de glace (A = 0) mais l’atmosphère absorbe désormais toute les radiations infrarouge émises (c’est-à-dire que τIR = 0) et la Terre chauffe jusqu’à 331K. Si nous réintroduisons les nuages et la glace dans l’exemple 4 (A = 0,3), la température redescend à 303K.
Questions possibles
Les questions typiques qui peuvent être posées, et qui pousseront les étudiants à utiliser ce modèle, sont :
- Laquelle des variables a les effets les plus significatifs sur la température moyenne globale?
- Si la distance moyenne Terre-soleil était augmentée de 1% de sa valeur actuelle, la constante solaire serait Quelle serait alors la température? Considérer que: albédo = 0,3, τIR = 0,3 et τVIS = 0,6.
(la constante solaire varie avec le carré de la distance, donc rapprocher la Terre du soleil de 10% porterait S à 1370/(0,9)2 = 1691 Wm-2 , et éloigner la Terre du soleil de 1% porterait S à 1370/(1,01)2 = 1343 Wm-2)
Bien sûr, des questions encore bien plus provocantes peuvent être posées.
- Si le sable du Sahara pouvait être remplacé par un miroir (le sable peut être fondu pour obtenir du verre),
- quelle taille devrait avoir ce miroir pour réduire la température de la planète de 1°C?
- quelle fraction du désert du Sahara cela représenterait-il?
Un modèle plus sophistiqué
Comment ce modèle simple peut il être comparé avec des modèles climatiques plus sophistiqués comme celui du centre Hadley utilisé par l’office météorologique du Royaume-Uni (voir les images ci-dessous)? En fait, les deux modèles sont très similaires, sauf que celui du centre Hadley ne considère pas une atmosphère à une seule couche, mais la divise en une série de boites définies par leur altitude, leur longitude et leur latitude. Pour chaque boite, le modèle calcule directement la quantité de radiations visibles et ultraviolettes incidentes transmises et réparties dans cette boite, et la quantité de radiations infrarouges émises sortant de cette boite, en se basant sur les concentrations des gaz à effet de serre principaux, et sur la surface des nuages et des glaces. Les versions les plus sophistiquées du modèle du centre Hadley considèrent aussi le flux de chaleur échangé avec l’océan et la recapture de CO2 par la végétation. Mais si l’on comprend les principes du modèle simple, on peut facilement saisir les modèles climatiques plus précis et compliqués.
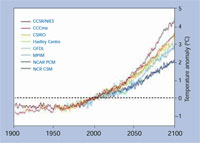
climatique; Prévisions de
réchauffement du modèle de
réchauffement global basées sur
les températures moyennes en
2000.Les données du modèle
sont issues du centre de diffusion
intergouvernemental de données
sur le changement climatique.
Image reproduite avec l’aimable
autorisation de Robert A. Rohde;
source de l’image: Wikimedia Commons
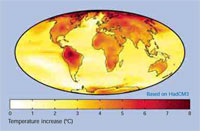
projections pour 2070-2100 d’après
les moyennes 1960-1990. Carte
prédictive du réchauffement
climatique à la fin du 21ème
siècle. Ce modèle prédit un
réchauffement moyen de 3°C,
et a été réalisé grâce au modèle
climatique du centre Hadley
HadCM3.
Image reproduite avec l’aimable
autorisation de Robert A. Rohde; source
de l’image: Wikimedia Commons
Participer à une vraie simulation climatique
Climateprediction.netw2 est la plus grande expérience tentant de produire une prédiction du climat du 21ème siècle. Ceci est rendu possible en demandant l’aide de personnes partout dans le monde, pouvant offrir du temps sur leurs ordinateurs- comme lorsque les ordinateurs sont allumés mais qu’ils ne sont pas utilisés au maximum de leurs capacités. Le modèle climatique complet comprend de nombreux paramètres qui doivent être ajustés; pour explorer tous ces paramètres, un nombre phénoménal de simulations doivent être réalisées. Même avec toutes les ressources informatiques disponibles pour l’équipe climateprediction.net, un tel ensemble de simulations prendrait énormément de temps. L’idée de climateprediction.net est que n’importe qui peut télécharger une version du modèle qui explorera un de ces paramètres particuliers (prédéfini). Il faudra environ 3 mois pour réaliser le programme, en arrière plan pendant que la personne travaille, sans altérer les performances de l’ordinateur.
Les calculs sont réalisés en trois étapes. La première étape utilise des données des années 1850 à 1900, comparant les résultats des prédictions avec les enregistrements de température: c’est la phase de calibrage. La seconde étape réalise une simulation de 1901 jusqu’à aujourd’hui. La troisième étape réalise une simulation du climat futur (2000-2100) avec un paramètre fluctuant, par exemple la sensibilité du climat aux incertitudes du cycle des sulfures. Quand les calculs sont terminés, les données sont automatiquement rechargées sur le site de l’office météorologique du Royaume-Uni lors de la prochaine connexion internet de l’ordinateur. Le logiciel d’interface fourni (gratuit) avec la simulation propose à l’utilisateur de l’ordinateur un graphique des changements du climat, tels qu’ils sont calculés. Les changements de températures à chaque saison par latitude, longitude et altitude sont certaines des variables qui peuvent être visualisées. Une telle opportunité peut permettre un projet scolaire interdisciplinaire alliant géographie et physique.
Dans le prochain numéro de Science in School, les auteurs proposeront des expériences de chimie en rapport avec le changement climatique.
Web References
- w1 – une version interactive du modèle climatique simple peut être utilisée en ligne ou téléchargée sur le site: www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- Utiliser les onglets pour changer les variables.
- w2 – pour plus de détails sur cette expérience, et pour participer, voir: http://climateprediction.net.
- Le site web climateprediction.net propose aussi des informations et des ressources spécifiques pour les scolaires, disponibles en anglais et en espagnol: http://climateprediction.net/content/resources-schools
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- De nombreuses fiches pour les enseignants, réalisées par les auteurs, sur la pollution de l’air, le changement climatique et le trou d’ozone sont disponibles sur: www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html
- Pour une excellente source de graphiques et de données relatives au changement climatique, voir: www.grida.no/climate/vital/index.htm
- Des données de la station de coordination générale du laboratoire de recherche sur le système Terre peuvent être trouvés sur: www.cmdl.noaa.gov
- Le site du rapport intergouvernemental sur le changement climatique, où le rapport du changement climatique 2007 et d’autres données peuvent être retrouvés, est: www.ipcc.ch
- Haubold B (2008) An Inconvenient Truth. Science in School 9: 72. www.scienceinschool.org/2008/issue9/inconvenient
Review
Le changement climatique devrait résolument faire partie des enseignements modernes de science à tous les niveaux scolaires partout en Europe. D’autant plus que, suite à l’énorme campagne menée par Al Gore avec «Une vérité qui dérange», les consciences ont été éveillées partout dans le monde sur ce thème. Cependant, les outils pédagogiques accompagnés de données scientifiques pour les enseignants ne sont pas toujours disponibles facilement. Cet article en deux parties propose une approche clef en main, facile à adapter, du processus compliqué de modélisation de l’évolution de l’atmosphère.
Alors que le modèle mathématique est mieux adapté à des étudiants de 16 ans et plus, engagés dans un cursus approfondi, les phénomènes simplifiés peuvent être présentés à des élèves de 15 ans ou même plus jeunes, même s’ils ne se destinent pas à des études scientifiques. Les ressources internet mentionnées offrent un large choix de protocoles et d’images prêtes à l’emploi, de liens informatiques et de graphiques, qui constituent une source d’information utile pour tout professeur de science.
Tobias Kirschbaum, Allemagne





