Costruire un modello del cambiamento climatico in classe Teach article
Traduzione di Massimo Bosetti – Museo Tridentino di Scienze Naturali, Laboratorio di Comunicazione delle Scienze Fisiche (Università degli Studi di Trento). Perché non permettere ai nostri studenti di fare le proprie “predizioni” del cambiamento climatico – con l'aiuto di Dudley…
Cambiamento climatico e riscaldamento globale sono diventati argomenti molto popolari e discussi che meritano un posto di rilievo nei curriculum scolastici di scienze. Come possiamo prevedere in quale direzione il clima cambierà? Sembra essere arrivato il momento in cui è possibile introdurre agli studenti i modelli climatici più semplici. In quest’articolo dimostriamo come gli studenti possono utilizzare un semplice foglio di calcolo per esaminare i principali fattori che influenzano il clima della Terra.
Un primo tentativo di costruire un modello del clima
Il modello climatico più semplice che possiamo ideare è quello in cui l’energia solare che arriva sulla terra è uguale all’energia uscente che il pianeta emette, quindi un modello d’equilibrio energetico “Energia entrante = Energia uscente”. In questo articolo con il termine “Energia” in realtà intendiamo dire “Flusso di Energia”, vale a dire energia per secondo per unità di superficie. Sappiamo dalle misure effettuate che l’energia (per secondo) solare che raggiunge la parte superiore dell’atmosfera, chiamata costante solare S, è di 1370 Wm-2.
Vogliamo cominciare calcolando la temperatura superficiale media della Terra: TE. Se la terra fosse perfettamente sferica e avesse raggio RE, in questo semplice modello, possiamo pensare che la Terra può assorbire la radiazione solare su di un’area uguale a πRE2 (quindi un disco piano di atmosfera) ed è capace di emettere energia, invece, da un’area pari a 4πRE2 (vale a dire tutta la superficie della Terra).
(a) Energia in = energia via
E usando la legge di Stefan-Boltzmann (vedi riquadro)
(b) Energia per unità di superficie per unità di tempo x superficie totale(disco) = energia per unità di superficie per unità di tempo x superficie totale(sfera)
(c) 1370 x πRE2 = σTE4 x 4πRE2
Modificando l’equazione si ottiene:
σTE4 = 1370 = S/4
4
TE4 = 1370
(4 x 5.67 x 10-8)
TE = 279 K (6 °C)
Dove σ è la costante di Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
A prima vista, per un modello così semplificato, sembra un valore ragionevole, anche se la temperatura superficiale media della Terra, realmente misurata, è noto essere di circa 16 °C (Esistono molti metodi per calcolare il valore medio, come ad esempio suddividendo la Terra in fasce di latitudine, calcolando la temperatura media per fascia e mediando i valori così ottenuti). Il problema con questo modello molto semplice, però, è che una parte dell’energia solare non è assorbita dalla Terra ma è, invece, riflessa indietro nello spazio dalle nubi prima, dal ghiaccio e dalla terra in seguito.
Approssimativamente il 24% della radiazione solare incidente è riflessa dalle nubi e un altro 6% è riflesso dalla superficie della terra, ad esempio, dal ghiaccio. Questo fa si che la riflettività totale della Terra – chiamata albedo (A) – sia di circa il 30% o 0.3. Pertanto, la parte sinistra dell’equazione (c) deve essere modificata così 0.7 x 1370 x πRE2 e la calculazione di TE diventa:
TE4 = 1370 x 0.7
(4 x 5.67 x 10-8)
TE = 255 K (-18 °C)
Questo valore è evidentemente troppo basso e conduce alla naturale domanda: Per quale motivo è così caldo sulla Terra? Al fine di rispondere a questa domanda abbiamo bisogno di un modello leggermente più complesso.
This value is obviously far too low, and leads naturally to the question: why is Earth so warm? In order to answer this question we need a slightly more complex model.
Conoscenze fisiche essenziali
La radiazione di corpo nero e la legge di Stefan-Boltzmann
Tutti i corpi irradiano energia sotto forma di radiazioni elettromagnetiche. Un corpo nero è un oggetto che assorbe tutte le radiazioni che incidono sul corpo stesso. Sappiamo, inoltre, che il corpo nero emette radiazioni elettromagnetiche in funzione della sua temperatura superficiale. La legge di Stefan-Boltzmann asserisce che l’energia totale, I, emessa da un corpo nero a una certa temperatura, T, è data da:
I(T) = σT4 (Equazione 1)
Dove:
I è l’energia per unità di area emessa al secondo (Wm-2)
T è la temperatura assoluta (K)
σ è la costante di Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
Black body radiation and the Stefan-Boltzmann Law
Il modello dell’atmosfera terrestre a strato singolo
Se assumiamo, per semplicità, che l’atmosfera sia costituita da un unico strato di gas miscibili, possiamo, con l’uso di un foglio di calcolo, sviluppare un modello molto più accurato del precedente. In questo modello si considera anche la parte di luce visibile, che arriva dal sole, e che è assorbita dall’atmosfera e la parte di radiazione infrarossa emessa dalla Terra che viene, a sua volta, assorbita dall’atmosfera.
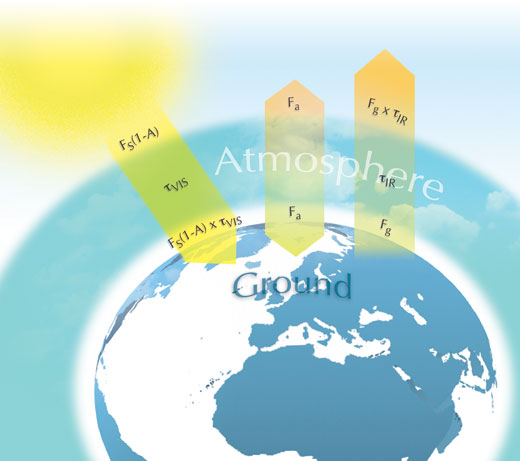
La figura riportata qui di seguito sintetizza gli elementi del modello. Fs è la costante solare divisa per 4 (S/4), che deriva dalla differenza tra l’energia che arriva su un disco di area πr2 e la radiazione uscente emessa dalla superficie della Terra di area 4πr2 (le ipotesi assunte nel primo modello). L’energia in arrivo dal sole è quindi FS(1-A), dove A è l’albedo – la parte riflessa indietro nello spazio. Questa radiazione incidente è maggiormente centrata nelle regioni UV e visibile dello spettro elettromagnetico. τVIS è la parte dell’energia, della radiazione visibile incidente, che non è assorbita dall’atmosfera: se l’atmosfera assorbisse tutto, τVIS sarebbe zero; se l’atmosfera non assorbisse nulla, allora. τVIS sarebbe uno. Per cui l’energia che raggiunge la superficie del pianeta è FS(1-A) x τVIS.
La terra comportasi in maniera simile a un corpo nero emette energia dalla sua superficie, che indichiamo con Fg a differenza della radiazione proveniente dal Sole, centrata maggiormente nella regione infrarossa dello spettro. Dobbiamo anche considerare che nell’atmosfera sono presenti alcuni gas capaci di assorbire la radiazione infrarossa: i gas serra. Questo porta ad una interazione tra i gas serra atmosferici e la radiazione emessa dalla terra in quanto corpo nero. In maniera simile a τVIS, τIR è la parte di energia assorbita dai gas atmosferici, relativa alla radiazione infrarossa, così l’energia uscente si scrive Fg x τIR.
Assumendo che l’energia proveniente dall’atmosfera sia Fa e che l’energia entrante e uscente dalla superficie della Terra e nella parte superiore dell’atmosfera siano entrambe in equilibrio, abbiamo quindi:
Sulla superficie della Terra:
FS(1-A) x τVIS + Fa = Fg (Equazione 2)
E nella parte superiore dell’atmosfera:
Fg x τIR + Fa = FS(1-A) (Equazione 3)
Combinando le equazioni 2 e 3:
Fg = FS(1-A)(1 + τVIS)
(1 + τIR)
Infine,
Fg = σTE4 = FS(1-A)(1 + τVIS)
(1 + τIR)
TE = [ FS(1-A)(1 + τVIS) ]0.25
[ σ(1 + τIR) ] (Equazione 4)
Se prendiamo i seguenti valori:
FS = 1370/4 = 342.5 Wm-2 (costante solare divisa per 4)
A = 0.3
τVIS = 0.8
τIR = 0.1
l’equazione 4 ci da:
TE = 288.5 K (15.5 °C),
Che è un’ottima approssimazione della temperatura superficiale media attuale della Terra.
È proprio l’Equazione 4 che può essere messa dagli studenti in un programma, come MS Excel o Openoffice.org Calc, in modo che possano essere osservati i cambiamenti della temperatura media globale quando vengono cambiati i valori dei parametri dell’equazione. Questo è possibile anche attraverso l’uso di un applet java interattivo scaricabile del sito web della Bristol Universityw1.
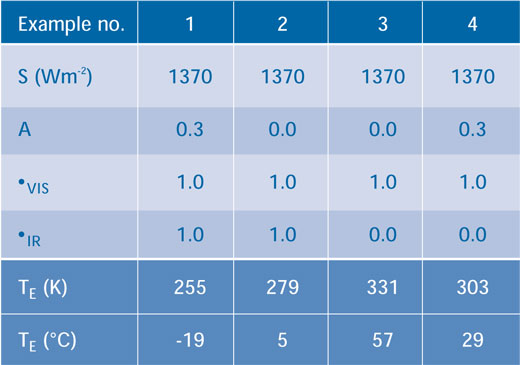
La Tabella 1 mostra alcuni esempi di risultati quando i parametri A, τVIS e τIR vengono modificati. Nell’Esempio 1 abbiamo assunto che l’atmosfera non assorba né la radiazione proveniente dal Sole (entrante) né la radiazione emessa dalla superficie della Terra (uscente), quindi entrambih τVIS e τIR are equasono posti uguali a 1.0) e l’albedo è 0.3. Questi valori dei parametri, messi nell’equazione, ci restituiscono una temperatura di 255 K. Nell’Esempio 2 abbiamo assunto che non vi siano nubi e la superficie della terra non rifletta nessuna radiazione, quindi A=0. Il risultato è una temperatura di 279 K, che mostra l’importanza dell’albedo sul clima. L’Esempio 3 è ancora ad albedo nullo, A=0, ma ora l’atmosfera è capace di assorbire tutta la radiazione infrarossa, quindi τIR = 0.0 e possiamo osservare come la temperatura si alzi a 331 K. Se ora modifichiamo l’albedo portandolo ad A = 0.3, Esempio 4, otteniamo una caduta della temperatura a 303 K.
Domande possibili
Tipiche domande che possono essere poste e che richiedono agli studenti l’uso di questo modello sono:
- Quale variabile ha il maggior effetto sulla temperatura globale media?
- Se la distanza media Terra-Sole aumentasse dell’1% rispetto al valore odierno, la costante solare diminuirebbe di un fattore 1.0201, quindi avrebbe un valore di 1343 Wm-2. Quale sarebbe la temperatura della Terra? Si assume che l’albedo sia 0.3, τIR 0.3 e τVIS 0.6.
(La costante solare varia come il quadrato della distanza Terra-Sole. Se avvicinassimo la Terra il 10% al Sole avremmo S = 1370/(0.9)2 = 1691 Wm-2 e se, invece, allontanassimo la Terra dal sole del 1% avremmo S = 1370/(1.01)2 = 1343 Wm-2).
Certamente molte altre domande possono essere poste.
- Se trasformassimo la sabbia del deserto del Sahara in vetro a specchio (la sabbia può essere sciolta in vetro),
- Quanto dovrebbe essere grande lo specchio per avere un raffreddamento del pianeta di 1 °C?
- Che frazione della superficie del deserto dovrebbe diventare vetro?
Un modello più sofisticato
Come funziona questo semplice modello in confronto ai modelli più raffinati come il modello dell’Hadley Centre usato dall’Ufficio Meteorologico della Gran Bretagna (vedi immagine sotto)? In realtà i due modelli sono molto simili, eccetto per il fatto che il modello dell’Hadley Centre non considera l’atmosfera come uno strato unico, ma la divide in un certo numero di celle sulla base della latitudine, longitudine e altitudine. Per ogni cella, il modello calcola direttamente la quantità di radiazioni, UV e visibile, entranti trasmesse e diffuse all’interno della cella, e la quantità di radiazione infrarossa uscente dalla cella, sulla base della concentrazione dei gas serra e della superficie di nubi e ghiaccio. I modelli più sofisticati del modello dell’Hadley Centre considerano anche il flusso di calore entrante e uscente dall’oceano e l’assorbimento di CO2 della vegetazione. Ma se si capiscono i principi alla base di questo modello semplice, si è sulla buona strada per capire i ben più complicati modelli climatici reali.
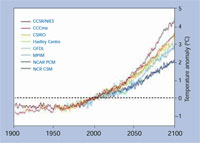
risclaldamento globale relative
alla temperature media globale
nel 2000. I dati del modello usati
sono presi dal Data Distribuition
Centre dell’IPCC.
Immagine cortesemente messa a
disposizione da Robert A. Rohde;
sorgete Wikimedia Commons
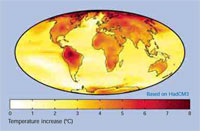
risclaldamento globale alla fine
del 21° secolo. Questo modello
Questo modello ha un
riscaldamento medio di of 3.0°C
e utilizza il modello climatico
HadCM3 dell’Hadley Centre.
Immagine cortesemente messa a
disposizione da Robert A. Rohde;
sorgete Wikimedia Commons
Prendere parte ad una simulazione climatica reale
Climateprediction.netw2 è il più grande esperimento per cercare di produrre una previsione per il clima del 21° secolo. A tal fine si cercano persone in tutto il mondo che facciano usare il loro computer – ad esempio quando il computer è acceso, ma non viene utilizzato al pieno delle capacità. Il modello climatico reale ha molti parametri che devono essere adattati e, quindi, un fenomenale numero di simulazioni deve essere eseguito. Anche con le risorse computazionali a disposizione di climateprediction.net, le varie simulazioni hanno bisogno di molto tempo. L’idea che sta dietro climateprediction.net è che ognuno può scaricare una versione del modello che studierà un particolare insieme di valori di parametri stabiliti in anticipo. Il modello lavorerà per circa tre mesi in background, senza compromettere la velocità del computer.
I calcoli sono svolti in tre fasi. Nella prima fase I calcoli usano i dati dal 1850 al 1900, confrontando i risultati delle previsioni e le temperature registrate: questa è conosciuta come fase di calibrazione. Nella seconda parte gira una simulazione dal 1901 ai giorni nostri. La terza fase simula il clima futuro (2000-2100) con uno dei parametri cambiati, per esempio la sensitività climatica alle incertezze del ciclo dello zolfo. Una volta completati, i calcoli, durante la prossima connessione internet vengono automaticamente scaricati all’Ufficio Meteorologico della Gran Bretagna. L’interfaccia del programma (liberamente scaricabile) assieme alla simulazione consente, al proprietario del computer, di vedere il grafico dei cambiamenti climatici così come sono stati calcolati. Le variazioni di temperatura stagionali, per latitudine, longitudine e altitudine sono alcune delle variabili che possono essere visualizzate. Tali caratteristiche permettono di sviluppare argomenti trasversali del curriculm collegando geografia e scienze fisiche.
Nel prossimo numero di Science in School, gli autori, suggeriranno alcuni importanti esperimenti di chimica in relazione al cambiamento climatico.
Web References
- w1 – Una versione interattiva del modello climatico semplice può essere utilizzata on line o scaricata qui: www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- Usa le slide per modificare i parametri.
- w2 – Per maggoiori dettagli sull’esperimento e come essere coinvolti, vedere http://climateprediction.net.
- Il sito web climateprediction.net offre anche informazioni e risorse specifiche per le scuole in lingua inglese e spagnolo. http://climateprediction.net/content/resources-schools
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- Numerose osservazioni per i docenti di scuola sull’inquinamento dell’aria, i cambiamenti climatici e l’assottigliamento dello strato d’ozono scritti dagli autori possono essere trovati sul sito: www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html
- Per eccellenti grafici e dati relativi ai cambiamenti climatici vdedere: www.grida.no/climate/vital/index.htm
- Molti dati del Earth System Research Laboratory Global Monitoring Station possono essere trovati qui: www.cmdl.noaa.gov
- Il sito internet del gruppo intergovernativo sul cambiamento climatico (IPCC), dal quale è scaricabile il report sui cambiamenti climatici del 2007, è: www.ipcc.ch
- Haubold B (2008) An Inconvenient Truth. Science in School 9: 72. www.scienceinschool.org/2008/issue9/inconvenient
Review
I cambiamenti climatici dovrebbero essere certamente uno degli argomenti dell’odierno insegnamento delle scienze in tutti i gradi di scuole d’Europa. Particolarmente dopo la campagna di Al Gore “Inconvenient Truth” l’argomento ha guadagnato peso nelle coscienze mondiali. Nonostante ciò, materiali utili con informazioni sul contesto climatico per gli insegnanti di scienze sono sempre di pronto disponibilità. Questo articolo, però, offre un approccio idoneo e facilmente adattabile ai complicati modelli climatici e atmosferici.
Nonostante i modelli matematici siano maggiormente adatti ad un uso in corsi di scienze avanzati per studenti con un’età maggiore di 16 anni, il fenomeno alla base può essere facilmente compreso anche da studenti di età inferiore, anche se essi non intendono specializzarsi in materie scientifiche negli anni successivi. Le risorse web indicate offrono un ampia varietà di approcci, immagini pronte all’uso, applet e grafici che sono uno strumento molto utile per ogni insegnante di scienze.
Tobias Kirschbaum, Germania





