Sınıfta iklim değişikliği modellemesi Teach article
Çeviri: Zeynep Gençyiğit, Hayrünisa Dere, Yusufcan Irmak, Canbolat Gürses, Hikmet Geçkil (Department of Molecular Biology and Genetics, Inonu University). İngiltere Bristol Üniversitesi’nden Dudley Shallcros ve Tim Harrison’un yardımıyla, öğrencileriniz iklim değişikliği ile…
İklim değişikliği ve küresel ısınma günümüzün ‘sıcak’ konularıdır ve bu nedenle iki konu da okuldaki fen dersi müfredatında önemli bir yerde olmayı hakediyor. Ancak iklimin değişeceğini nasıl tahmin ederiz? Basit iklim modellemesini öğrencilere tanıtmanın tam zamanı. Bu makalede, öğrencilerin dünya iklimini etkileyen ana faktörleri inceleyebilmeleri için basit bir çizelgenin nasıl kullanılabileceğini göstereceğiz.
İklim modellemesi için ilk adım
İklimin en basit modellemesi, gelen güneş enerjisi ile gezegen tarafından yayılan yani uzaklaşan karasal enerjinin birbirine eşit olduğudur. Yani ‘giren enerji çıkan enerjiye eşittir’. Bu makalede, ‘enerji’ terimi gerçekte enerji akışı anlamına gelmektedir (örn. Bir saniyedeki enerji). Ölçümlerden bildiğimiz üzere, güneşten gelen ve bir saniyede atmosferin en üst noktasına ulaşan enerji, güneş sabiti S olarak bilinen 1370 Wm-2’dir.
Dünyanın ortalama yüzey sıcaklığını (TE) hesaplayarak başlayalım. Eğer kusursuz küresel biçimdeki Dünya’nın yarıçapını RE olarak (yani atmosferik düz bir disk) kabul edersek, bu basit modelde Dünya’nın, bir πRE2 alanı üzerindeki güneş radyasyonunu emdiği görülebilir ama enerjiyi 4πRE2 gibi bir alandan (yani tüm yüzeyden) yayar.
(a) Alınan enerji= Verilen enerji
ve Stefan-Boltzmann Yasasını kullanarak (kutuya bakınız)
(b) Birim zamanda birim alandaki enerji x toplam alan(disk) = birim zamandaki birim alandaki enerji x toplam alan(küre)
(c) 1370 x πRE2 = σTE4 x 4πRE2
Yeniden düzenlenmiş denkleme göre:
σTE4 = 1370/4 = S/4
TE4 = 1370/(4 x 5.67 x 10-8)
TE = 279 K (6 °C)
Burada σ, Stefan-Boltzmann sabitidir (5.67 x 10-8 Wm-2K-4).
İlk bakışta, böylesine kaba bir model için anlamlı bir şekil gibi görünse de, Dünya’nın gerçek ortalama yüzey sıcaklığının 16°C derece olduğu bilinmektedir (Bunu anlamamızı kolaylaştıracak birkaç yöntem bulunmaktadır. Dünyanın enlem kuşaklarına bölünmesi, kuşak başına ortalama sıcaklığın hesaplanması ve hepsinin toplanıp ortalamasının alınması örnek olarak verilebilir). Bu basit modeldeki sorun, güneş enerjisinin bir kısmının bulutlar ve buz tarafından geri yansıtılması sonucu Yer Küre tarafından absorbe edilmemesidir.
Gelen enerjinin yaklaşık olarak %24’ü bulutlar tarafından yansıtılırken, diğer bir %6’sı da yüzey (örneğin buz) tarafından yansıtılmaktadır. Bu durum albedo (A) olarak bilinir ve dünyanın toplam %30 veya 0.3 yansıtma özelliğini belirtir. Bundan dolayı, denklemin sol tarafı (c) 0.7 x 1370 x πRE2 şeklinde yeniden yazılmalıdır ve TE’nin hesaplanması şu hale gelir:
TE4 = (1370 x 0.7) / (4 x 5.67 x 10-8)
TE = 255 K (-18 °C)
Bu değer açıkça çok düşüktür ve doğal olarak şu soruya cevap aramaya yöneltmektedir: Neden Dünya bu kadar sıcak? Bu soruyu cevaplamak için biraz daha karmaşık bir modele ihtiyacımız vardır.
Temel Fizik
Siyah cisim radyasyonu ve Stefan-Boltzmann Yasası
Bütün cisimler enerjiyi elektromanyetik radyasyon şeklinde yayarlar. Siyah cisimler, üzerlerine düşen bütün radyasyonu absorbe eder ve radyasyonu yüzey sıcaklığının bir fonksiyonu olarak yayarlar.Stefan-Boltzmann Yasası, herhangi bir T sıcaklığında siyah bir cisim tarafından yayılan toplam enerjiyi (I) şu şekilde açıklar:
I(T) = σT4 (Denklem 1)
Bu denklemde,I, saniyede yayılan birim alan başına enerji (Wm-2)
T, mutlak sıcaklıktır (K)
σ ise Stefan-Boltzmann sabitidir (5.67 x 10-8 Wm-2K-4).
Dünya’nın tek katmanlı atmosfer modeli
Atmosfer tabakasını birbiri içinde karışabilen gazlardan oluşan tek tabakalı olarak varsayarsak, öğrencilerin grafik şeklinde kullanabileceği daha doğru bir model oluşturabiliriz. Bu modelde, Güneşten gelen görünür ışığın atmosferi ve Dünyadan yayılan kızılötesi ışığın absorbsiyonu hesaba katılır.
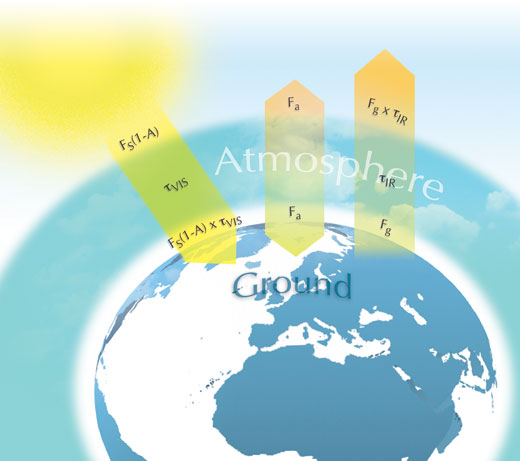
Aşağıdaki şekil modelin unsurlarını özetlemektedir. FS, bir disk üzerinde (πr2) dağılmış olan gelen enerji ile bir kürenin yüzeyinden (4πr2) (ilk modelde yapılan varsayımdan yola çıkarak) yayılan enerji arasındaki farktan kaynaklanan güneş sabitinin 4’e bölümüdür (S/4). Güneşten gelen enerji FS(1-A)’dır, burada A albedo’dur (yani uzaya geri yansıtılan kısım). Bu gelen enerji UV’de ve görünür bölgelerdedir. τVIS, bu gelen enerjinin atmosfer tarafından soğurulmayan kısmıdır. Eğer atmosfer hepsini soğurursa, τVIS sıfır olur. Atmosfer hiçbirini soğurmaz ise, τVIS bir olur. Bundan dolayı, gezegenin yüzeyine ulaşan enerji FS(1-A) x τVIS’dir.
Yerküre, kara maddeye benzer davranacaktır ve yüzeyinden Fg olarak gösterilen enerjiyi yayacaktır. Bu karasal radyasyon, spektrumun (şua) kızılötesi bölgesinin merkezindedir. Atmosferdeki belirli gazlar (sera gazları) kızılötesi enerjiyi soğurur. τVIS’a benzer bir şekilde τIR atmosferde bu gazlar tarafından soğurulmayan kızılötesi enerjinin bir ksımıdır ve böylece dışarı salınan enerji Fg x τIR’dir.
Earth will behave similarly to a black body and will emit the energy denoted as Fg from its surface. This terrestrial radiation is centred in the infra-red region of the spectrum. Certain gases in the atmosphere absorb the infra-red energy (greenhouse gases). Similar to τVIS, τIR is the proportion of infra-red energy not absorbed by these gases in the atmosphere, and so the outgoing energy is Fg x τIR.
Atmosferin enerjisini Fa olarak gösterir ve dünyanın iç ve dış yüzeyindeki enerji ve atmosferin üstündeki bu enerjinin ikisinde de dengede olduğunu varsayarsak:
Dünyanın yüzeyinde:
FS(1-A) x τVIS + Fa = Fg (Denklem 2)
ve atmosferin üzerinde:
Fg x τIR + Fa = FS(1-A) (Denklem 3)
2 ve 3. Denklemlerin birleşimi sonuçta şunu verir:
Fg = (FS(1-A)(1 + τVIS)) / (1 + τIR)
Sonuç olarak,
Fg = σTE4 = (FS(1-A)(1 + τVIS)) / (1 + tIR)
TE = [(FS(1-A)(1 + τVIS)) / σ(1 + τIR)]0.25 (Denklem 4)
Aşağıdaki değerleri alırsak:
FS = 1370/4 = 342.5 Wm-2 (güneş sabiti 4’e bölünmüş)
A = 0.3
τVIS = 0.8
τIR = 0.1
Denklem 4 bize şunu verir:
TE = 288.5 K (15.5 °C),
Bu, Dünya’nın şu andaki ortalama yüzey sıcaklığına yakın bir tahmindir.
Denklem 4 Microsoft Excel gibi bir programa koyulabilinir böylece öğrenciler denklemdeki parametreleri değiştirdikçe küresel ısınmadaki değişimleri görebilir. Bunun interaktif (etkileşimli) versiyonu çevrimiçi olarak Bristol Üniversitesinin internet sitesindenw1 indirilebilir.
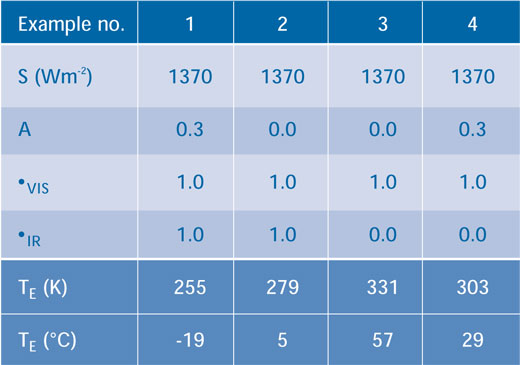
Değişkenler A, τVIS ve τIR değiştirilirse, Tablo 1 çıktı örneklerini gösterir. Birinci örnekte atmsoferin giren ve çıkan hiçbir enerji akışını soğurmadığını (yani hem τVIS hem de τIR 1.0’a eşittir) farzediyoruz ve albedo 0.3 olup 255 K’lik bir sıcaklık verir. Ikinci örnekte, hiçbir buz veya bulutun olmadığını varsayıyoruz (yani, A=0.0). Bu, dünyanın sıcaklığını 279 K’e çıkarmakta ve albedo’nun önemini göstermektedir. Üçüncü örnekte, yine hiçbir buz veya bulut yok fakat atmosfer bu defa tüm giden kızılötesi radyasyonları absorbe ediyor (yani, τIR = 0.0) ve dünya 331 K’ne ısınıyor. Şimdi Dördüncü örnek (A = 0.3), bulut ve buzları yeniden devreye sokarsak sıcaklık 303 K’e düşer.
Muhtemel sorular
Sorulabilecek ve öğrencilerin bu modeli kullanmasını gerektiren tipik sorular şunlardır:
- Ortalama küresel sıcaklığın üzerinde en büyük etkiye sahip değişkenler hangileridir?
- Dünya ile Güneş arasındaki ortalama mesafenin mevcut değeri %1 artsaydı, güneş sabiti 1.0201 faktör kadar azaltılacak, yani 1343 Wm-2 olacaktı. Sıcaklık ne olurdu? (bir albedo’yu 0.3, τIR 0.3 ve τVIS 0.6 varsayınız).
(Güneş sabiti, mesafenin karesi ile ölçeklenecek, yani Dünya’nın Güneş’e %10 daha yakın hareket etmesi anlamına gelecektir; S = 1370 / (0.9)2 = 1691 Wm-2 ve Dünya’nın %1 daha uzaklaşması demek; S = 1370 / (1.01)2 = 1343 Wm-2)
Elbette, çok daha zorlayıcı sorular sorulabilir.
- Sahra Çölü’ndeki tüm kumla bir cam ayna yapılsa (kum, cama eritilebilir),
- Gezegeni 1°C soğutmak için aynanın ne kadar büyük olması gerekir?
- Bu, Sahra Çölü’nün ne kadarlık bir parçası olurdu?
Daha sofistike bir model
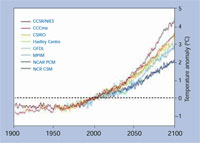
projeksiyonları; 2000’deki
küresel ısınmada ortalama
küresel sıcaklık için iklim
modeli tahminleri. Kullanılan
model verileri, İklim
Değişikliği Veri Dağıtım
Merkezi üzerinden bir
Hükümetler Arası Panelden
alınmıştır. Resmi büyütmek için tıklayınız.
Robert A. Rohde’un izniyle;
görüntü kaynağı: Wikimedia
Commons
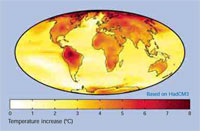
2070-2100 tahmini ve 1960-
1990 ortalaması
21. yüzyılın sonunda tahmin
edilen küresel ısınmanın bir
haritası. Bu model ortalama
3.0°C’lik bir ısınma
öngörüyor ve Hadley Center
HadCM3 iklim modelini
kullanıyor. Resmi büyütmek
için tıklayınız.
Robert A. Rohde’un izniyle;
görüntü kaynağı: Wikimedia
Commons
Basit bir model, daha karmaşık olan Birleşik Krallık Meteroloji Ofisindeki (aşağıdaki resimlere bakınız) Hadley Merkezi iklim modeli ile kıyaslanabilir? Aslında, bir şey hariç olmak üzere iki model birbirine çok benzerdir; Hadley merkezi modelinde atmosfer tek katmanlı olarak kabul edilmemekte ve enlem, boylam ve rakıma dayalı bir dizi kutucuğa ayrmaktadır. Her bir kutu için, gelen UV/görünür radyasyondan iletilen ve kutu içerisinde saçılan miktarını ve giden kızılötesi radyasyonun bu kutu tarafından iletilen miktarını sera gazlarının yoğunluğuna, bulut ve buzun yüzey alanına dayanarak doğrudan hesaplar. Hadley Merkezi modelinin en gelişmiş versiyonları okyanusa giren ve çıkan ısı akışını ve bitki örtüsü tarafından CO2 alımını da göz önüne alır. Fakat basit modelin ilkelerini anlarsanız, daha karmaşık gerçek iklim modelini anlamada iyi yolda ilerliyorsunuz demektir.
Gerçek iklim simülasyonuna katılmak
Climateprediction.netw2, 21. yüzyılda iklim tahmini yapmak için geliştirilmiş en büyük deneydir. Bu proje, bilgisayarlarının kapasitelerini tamamen kullanmayan dünyanın dört bir yanında gönüllünün bilgisayarlarını açık bırakıp bu hesaplamalara yardımcı olmaları yürütülmektedir. Tam iklim modelinde ayarlanabilen birçok parametre vardır. Bu parametrelerin hepsini keşfetmek için olağanüstü sayıda simülasyon yapılmalıdır. Climateprediction.net ekibi için bilgisayar kaynakları uygun olsa bile, böyle çok sayıda simülasyon uzun zaman alacaktır. Climateprediction.net’in arkasındaki fikir, herhangi birinin bu belirli parametrelerden birini keşfedecek bir modelin sürümünü indirebilmesidir. Modelin bilgisayarın hızından ödün vermeden, siz çalışırken arka planda çalışmaya devam etmesi yaklaşık üç ayı bulacaktır.
Hesaplamalar üç aşamada gerçekleştirilmektedir. İlk aşamada, 1850-1900 yılları arasındaki verileri kullanarak tahmin sonuçlarını sıcaklık kayıtlarına karşı kontrol edip hesaplamaları yapar: bu süreç, kalibrasyon çalışması olarak bilinir. İkinci aşama, 1901’den günümüze kadar bir simülasyon çalıştırmaktadır. Daha sonra üçüncü aşama ise bir parametrenin değiştirilmesiyle, örneğin kükürt döngüsündeki belirsizliklere iklimin duyarlılığı, gelecekteki iklimin (2000-2100) simülasyonunu gerçekleştirir. Hesaplamalar tamamlandıktan sonra veri, Birleşik Krallık Meteoroloji Bürosu’nun bilgisayarı çevrimiçi olduğunda otomatik olarak yüklenir. Simülasyon ile sağlanan arayüz yazılımı (ücretsiz) bilgisayar kullanıcısına, iklimin hesaplanmasıyla ortaya çıkan değişiklikler grafiğini verir. Mevsime göre sıcaklık değişimleri enlem, boylam ve rakımla görselleştirilebilen bazı değişkenlerdir. Bu özellikler, coğrafya ve fiziksel bilimler arasında bağlantı kurarak bir çapraz müfredatlı okul projesini mümkün kılar.
Science in School‘un sonraki sayısında, çeşitli yazarlar iklim değişikliği ile ilgili bazı kimya deneyleri önermektedirler.
Web References
- w1 – Basit iklim modelinin interaktif bir versiyonu çevrimiçi olarak kullanılabilir veya buradan indirilebilir:www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- Değişkenleri değiştirmek için sürgüleri kullanın.
- w2 – Deney ve deneye nasıl dahil olabileceğiniz hakkında daha fazla detay için bakınız: http://climateprediction.net.
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- Hava kirliliği, iklim değişikliği ve ozon tabakasının azalması hakkında çeşitli yazarlar tarafından öğretmenler için sayısız not burada bulunmaktadır:www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html
- İklim değişikliği ile ilgili mükemmel grafikler ve veri kaynakları için bakınız: www.grida.no/climate/vital/index.htm
- Dünya Sistem Araştırma Laboratuvarı Küresel İzleme İstasyonu’ndan elde edilen veriler şu adreste bulunabilir: www.cmdl.noaa.gov
- İklim Değişikliği 2007 raporunun ve diğer verilerin yer alabileceği Hükümetler Arası İklim Değişikliği Paneli’nin web sitesi: www.ipcc.ch
- Haubold B (2008) Uygunsuz Gerçek. Science in School 9.
Review
İklim değişikliği, Avrupa’daki tüm okullarda bugünün fen öğretiminin başlıklarından biri kesinlikle olmalıdır. Özellikle Al Gore’un muazzam Uygunsuz Gerçek kampanyasından sonra konu dünya çapında tanınır hale geldi. Ancak, fen öğretmenlerinin kullanabileceği arka planda neler olduğunun bilgisini içeren yararlı malzemeler her zaman mevcut değildir. Oysa bu iki bölümlü makale, atmosferik gelişmelerin modellenmesi için oldukça karmaşık bir sürece nazaran uygun ve kolay uyarlanabilir bir yaklaşım önermektedir.
Buna karşılık, 16 yaş ve üzerindeki öğrencilerin yararına ileri düzey fen derslerinde kullanılmak için en uygun olanı matematiksel modeldir. Hatta daha sonraki okul yıllarında bilimde uzmanlaşmak istemeseler bile, 15 veya daha genç yaştaki öğrenciler için temel olgular kolaylıkla sunulabilir. Bahsedilen internet kaynakları, kullanıma hazır görüntülerin, basit uygulamaların ve grafiklerin yanısıra çok geniş bir yaklaşım sunmaktadır. Böylece, herhangi bir fen öğretmeni için çok yararlı kaynaklar sağlanmaktadır.
Tobias Kirschbaum, Almanya





