Weighing up the evidence: what is a kilo? Understand article

​We all know what a kilogram is – or do we? Researchers worldwide are working to define precisely what this familiar unit is.

How much does it weigh? What is its surface area? What is its temperature? These questions may seem simple but the answers only make sense when we have defined a value and a unit.

The more widely accepted this unit is, the better the measurements are understood. Just imagine – if I walked seven furlongs to work this morning and you travelled 10 km, who had the longest journey? This is why we need an international system of units.

The first unit to be internationally defined was the metre (figure 1). It also led to the first international agreement on units, when the 1875 Convention of the Metre in Paris, France, established the International Bureau of Weights and Measures (BIPM, or Bureau International des Poids et Mesures) – an organisation that exists to this day.

Initially, the only common units were for length and mass, but the system has evolved over the years. Thus the initial set of units for length and mass was extended to include the standards of electricity, photometry and radiometry, ionising radiation, time and chemistry. The complete set of standardised units is referred to as the International System of Units^w1 (SI for Système International d’Unités).

The SI is based on the metric system and consists of both base units and derived units. The seven base units^w2 define a system of independent quantities and their units (see box on definitions of SI base units). The derived units of the SI define all other quantities in terms of the base units. For example, the SI unit of force, the newton, is defined as the force that accelerates a mass of one kilogram at the rate of one metre per second squared.

A universal system?

A universal set of units has clear advantages, but there is still some way to go before the SI is established globally and to the exclusion of all other systems. Initially established by 17 countries, the BIPM now has 55 member states. Nonetheless, the degree to which the SI has been adopted varies between the members. In both the UK and the USA, for example, miles, pints, and degrees Fahrenheit are still commonly used. Furthermore, even in fully metrified countries, some non-SI units remain popular. These include the minute, day and hour, as well as the hectare, litre and tonne.

The case of the kilogram

The kilogram is the only one of the seven base units to have a prefix (‘kilo’) in its name. It is also the only one that is still officially defined by a material artefact – all others are defined by fundamental constants or atomic properties (see box on definitions of SI base units). The international prototype of the kilogram is a cylinder of platinum-iridium alloy, machined in 1878 and preserved at BIPM (figure 2).

Over the years, several official copies have been produced and distributed to various national metrology offices (metrology is the scientific study of units and measurement). With the aid of modern technology, the mass of the prototype and its copies can now be compared with very high precision (up to 1 microgram), revealing significant variation (figure 3).

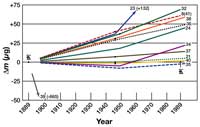
It is, therefore, high time for an absolute definition of the kilogram. This will not involve changing the mass of the kilogram. What will change is the way in which the kilogram is defined: rather than being defined as the mass of an object stored in a Paris vault, it will be a reproducible definition based on atomic properties and fundamental constants. Using this new definition, a well equipped laboratory will be able to create from scratch, without reference to the prototype, an object that weighs exactly 1 kg. Or, of course, to test and calibrate scales very precisely.

Furthermore, redefining the kilogram will also affect three other base units: the ampere, the mole and the candela, the definitions of which depend on the kilo (see box on definitions of SI base units).

Since the 1990s, several approaches have been pursued, two of which seem promising. Both involve defining the kilogram in terms of an invariant natural quantity: in one case the Avogadro constant, in another, the Planck constant. Both of the approaches also involve measuring the relevant constant to an unprecedented degree of precision.

Defining the kilogram in terms of the Avogadro constant

The aim of the international Avogadro project is to define the kilogram as the mass of a specific number of carbon-12 atoms. Under the current definition, Avogadro’s number is the number of atoms in 0.012 kg of carbon-12. Thus if we rearrange the equation, we could define a kilogram as the mass of an Avogadro number of carbon-12 atoms x 1000 / 12.

To do this, the project team aims to measure the value of the Avogadro constant (N_A, which has the same numerical value as the Avogadro number, expressed in moles) more precisely than ever before.

At the heart of the project is a nearly perfect sphere of silicon (figure 4) weighing exactly 1 kg, as defined by the platinum-iridium prototype. Silicon, rather than carbon-12, was chosen because large, high-purity and almost perfect single crystals can be produced.

The scientists are using a variety of techniques to determine the distance between atoms (the lattice parameter), the crystal density and the mean molar mass of the silicon (which has several isotopes). Using these data, they will be able to calculate the number of atoms in the 1 kg silicon sphere and derive a new and more precise measurement of the Avogadro constant. This could then be used in a new definition of the kilogram (Andreas et al., 2011; Becker et al., 2003):

1 kg = atomic mass of C-12 x 0.0012 x N_A

Defining the kilogram in terms of the Planck constant

The other approach to defining the kilogram uses a watt balance^w3, ^w4. The watt balance, which compares mechanical and electrical energy, was invented in 1975 and used in the 1980s to better determine the Planck constant by weighing the platinum-iridium prototype of the kilogram. Then scientists realised they could turn the idea around and use the instrument to define the kilogram.

Currently, the Planck constant has been measured to be:

h = 6.626 068 96 x 10^-34 kg m² s^-1

The values of fundamental constants, such as the Planck constant, are invariants of nature. However their numerical values (e.g. 6.626 068 96 x 10^-34) depend on the units (e.g. kg, m, and s) in which they are expressed. Fixing the numerical value of the constant therefore defines the units. In the case of the Planck constant, the metre and second are already defined in the SI. As can be seen in the equation above, therefore, precisely measuring the Parisian kilogram prototype – as will be possible with the watt balance – will allow h to be measured more precisely than before. Once that value is fixed, the kilogram can then be defined in terms of h, m and s, independently of the original prototype.

Worldwide, several metrology institutes are working to develop increasingly precise watt balances. One project, led by the Swiss Federal Institute of Metrology (METAS), includes CERN (see box), which is developing a type of magnet^w3 that is crucial to the operation of the balance. The aim of all the watt balance projects is to reach a new definition of the mass unit – known provisionally as the electronic kilogram – by reducing the uncertainty in their experimental setups to ≤ 5 x 10^-8. This, however, is no mean feat, due to the precision of the measurements and complexity of the instruments required.

The outlook

So which of the two approaches will be used to redefine the kilogram? At the BIPM’s 24^th general conference on weights and measures in 2011, it was proposed that the definition based on the Planck constant should be used. Nonetheless, if the proposal were accepted, the work on the Avogadro constant would not go to waste. For one thing, the Avogadro constant may be used in a new definition of the mole^w5. And for another, the Avogadro constant provides an alternative method to determine the Planck constant^w6 – thus indirectly feeding into the definition of the kilogram. But that is another story.

More about CERN

The European Organization for Nuclear Research (CERN)^w7 is one of the world’s most prestigious research centres. Its main mission is fundamental physics – finding out what makes our Universe work, where it came from, and where it is going.

CERN is a member of EIROforum^w8, the publisher of Science in School.

Acknowledgement

The authors would like to thank Simon Anders, a physicist based at the European Molecular Biology Laboratory, for his helpful comments on the article.

References

• Andreas B et al. (2011). Counting the atoms in a ²⁸Si crystal for a new kilogram definition. Metrologia 48(2): S1-13. doi: 10.1088/0026-1394/48/2/S01
• Becker P et al. (2003) Determination of the Avogadro constant via the silicon route. Metrologia 40: 271-287. doi: 10.1088/0026-1394/40/5/010
• Girard G (1994) The third periodic verification of national prototypes of the kilogram (1988-1992). Metrologia 31: 317-336. doi: 10.1088/0026-1394/31/4/007

Web References

• w1 – The definitive international reference on the SI is published in French, although an English translation is also available.
• w2 – Learn more about the seven base units of the SI system.
• w3 – Download an explanation of the watt balance (in Word^® or as a PDF).
• w4 – Visit the BIPM website for more details of the watt balance.
• w5 – Learn more about how the kilogram and the mole may be redefined.
• w6 – Learn more about the international Avogadro project.
• w7 – More information about CERN.
• w8 – EIROforum is a collaboration between eight of Europe’s largest inter-governmental scientific research organisations, which combine their resources, facilities and expertise to support European science in reaching its full potential. As part of its education and outreach activities, EIROforum publishes Science in School.

Institutions

Author(s)

Dr Eleanor Hayes is the editor-in-chief of Science in School. She studied zoology at the University of Oxford, UK, and completed a PhD in insect ecology. She then spent some time working in university administration before moving to Germany and into science publishing in 2001. In 2005, she moved to the European Molecular Biology Laboratory to launch Science in School.

Dr Marlene Rau was born in Germany and grew up in Spain. After obtaining a PhD in developmental biology at the European Molecular Biology Laboratory, she studied journalism and went into science communication. Since 2008, she has been one of the editors of Science in School.

Review

This article highlights the importance of having and using an international system of units. It could be very suitable for introductory lessons in physics or chemistry, and could also be used in non-scientific subjects such as languages and history to explain how important it is to follow established conventions (e.g. grammar).

Before reading the text, the following questions could be asked to students to make them start thinking about the concepts explained in it:

1. Is it important to have standard measurement units in science?
2. When do you think the international system of units was established?
3. What could happen if scientists do not use standard units?
4. Can you find an analogy between the international system of units and a concept in a non-scientific subject such as English, history or art?

As the article includes some historical data of the evolution of the international system of units, it could be used for a discussion of the history of science, a topic rarely seen in secondary school. Moreover, these historical details could make students who are not usually keen on science read the article with interest.

Mireia Güell Serra, Spain

License

CC-BY-NC-ND