Damn lies Understand article
Do you have more than the average number of ears? Is your salary lower than average? When will the next bus arrive? Ben Parker attempts to convince us of the value of statistics – when used correctly.

number of ears?
Image courtesy of Lisa Kyle
Young/iStockphoto
Whether it was Mark Twain or Benjamin Disraeli who first coined the idea that there are three types of falsehood – “Lies, damned lies, and statistics” – the sentiment still persists. Statisticians are manipulative, deceitful types, set to pollute our minds with meaningless and mendacious information that will make us vote for their favourite political party, use their demonstrably effective skin cream, or buy the pet food that their cats prefer. For me, as a statistician, it’s now time to debunk a few myths.
Exactly 96.4% of our modern world revolves around statistics, and although there are some shockingly bad statistics out there, I hope to convince you that the fault lies generally in their presentation.
Ear we go
I could make a confident bet that you, gentle reader, have more than the average number of ears. Why? Let’s assume that there are six billion people in this crowded world of ours, more than 99% of whom have two ears. There are a few exceptional people who, due to injury or birth, may have one or even no ears. There are, to my knowledge, no three-eared people (Captain Kirk is unfortunately fictional, but he did have three ears: a left ear, a right ear, and a final front ear). When we take an average (add up the total number of ears that humanity possesses, and divide by the number of people), we get the sum
Slightly less than 12 billion/6 billion
which is slightly less than two. This means that, as most people in the world have two ears, they have very slightly more than the average, so most times I would win my bet.
What does this mean?
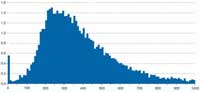
weekly income 2004/2005:
Number of individuals
(millions), Great Britain. Click
to enlarge image
Source: Households Below
Average Income (HBAI)
1994/95-2004/05,
Department for Work and
Pensions.
Now, of course, this is obviously just a statistician being pedantic. However, slightly less silly examples abound. Statistics on how one group of people earn less than a certain percentage of the national average income are used as political footballs. It is all too common to read commentaries in newspapers about how shocking it is that people earn only a percentage of the national income, and it’s all the fault of the Labour government, previous Conservative administration, European Union or sunspots.
The distribution of incomes, according to the UK Department for Work and Pensions (see figure to the right), is such that there are relatively few people who earn large sums of money (unfortunately statisticians do not fall into this high-income group). This means that the average income, which the Department has calculated to be £427 per week for a couple with no children (DWP, 2006), is much more than what the majority of people earn, in parallel with the above explanation of average ear count. A few extraordinary people, whether they have fewer than two ears or earn large amounts of money, skew the average from the situation for the majority of people.
Now of course, people soon realised that this commonly used average, calculated by adding everything up and dividing by the number of things you added up, more properly referred to as the mean, was likely to be misinterpreted. So the concept of the median is one that is often used in practice. If we were to put all the people in the UK in a line according to their income, the median salary would be that which the person standing in the middle of the line would have. The median, about £349 per week in this example, in practice often gives a better idea about what is typical.
At least we have reached some common sense – so can we expect everyone to understand this fairly basic problem in conveying ideas with averages? After all, surely the role of a good journalist is to take ideas and present the truth in a way the public can understand?
Unfortunately, factual accuracy and correctly interpreting data sometimes don’t sell newspapers, or make the correct political point.
Ironing out the wrinkles

was satisfied
Image courtesy of Al Wekelo
/iStockphoto
Worse than journalists, but not quite as bad as politicians, are advertisers. A recent television advert for a cosmetics company claims that their latest wrinkle-removing cream satisfies 8 out of 10 customers, based on a survey of 134 people. We can perhaps excuse the small sample size – and even the rounding (134 x 8/10 = 107.2), which means they must have found 0.2 of a customer to try out the cream – but the crucial question is how did they do the survey?
It seems to me that asking 134 customers whether they like the product is dubious – if the people are already customers, and have bought the product voluntarily, perhaps it’s not the fairest sample in the world. Why would anyone buy the product who doesn’t like it? In most sensible scientific trials, one would hope to compare the performance of the cream objectively against a brand X cream, or a placebo, to see whether people chosen at random have had a positive effect with the cream.
There’s no problem with advertising per se; philosophers argue that advertising is the most vital thing for a strong democracy. It’s fine for advertisers to let people know about their product and promote its benefits. However, what’s not acceptable is putting a thin veneer of science around the marketing; although cunningly worded, without explaining the method, the statistic ‘8 out of 10’ is meaningless. It’s just as bad as saying “Our car has a top speed of 500 miles an hour” without adding that this speed is only obtainable when measuring how fast the car drops out of an aeroplane: it’s true, but it’s misleading. Using this kind of fake survey in advertising is paramount to lying.
Three come along at once
Maybe it’s unfair to blame the conveyors instead of the statistics themselves. There are some real, difficult, non-intuitive facts that statistics throws up, the truth of which can be very hard to work out. Let’s say you’re waiting for a bus, and you look at the schedule, which, assuming it hasn’t been vandalised, tells you that there are five buses an hour. How long would you expect to wait for a bus?
Sensible logic tells us that if there are 5 buses an hour, then the average (sorry, mean) time between buses is 12 minutes. So, assuming you arrive at the bus stop at a random time within this period, you’d expect to wait 6 minutes for a bus. Good logic, but unfortunately, in general, wrong.
We know that buses don’t run to the minute. They may leave the depot on time, but chance factors will alter their progress in different ways, so we have to assume that the incoming pattern at our bus stop varies somewhat. What exact distribution we choose might vary – we may, for example, assume that times between arrivals of buses follow an exponential distribution – but the important fact is that the buses do not come at regular times. So let us now assume that we arrive at the bus stop at some random point in time – how long is our expected wait for a bus now?
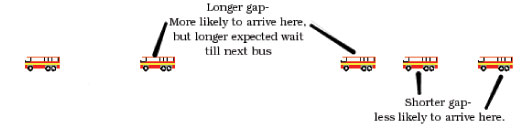
Image courtesy of Ben Parker
When we turn up at the bus stop, we are more likely to pick a period when there is a big gap between buses – a big gap occupies more time than a small gap, so we’re more likely to get a big one when picking at random. But given that we’ve picked a big gap, we know that the length of gap is more than 12 minutes (there are still 5 buses an hour) – so the average time to wait, given that our exact arrival time is equally likely to be somewhere in the big gap, is more than 6 minutes.
This is known as the inspection paradox, and it’s tricky to get your head around it. However, it’s a real phenomenon that is used by traffic planners and operational researchers, who are responsible for working out the most efficient method of arranging queues in post offices, and then ignoring it totally.
Are the bus companies wrong to advertise, then, that they have a bus approximately every 12 minutes? I think so, although it’s difficult to convey all the gory details of the inspection paradox; perhaps in this case we can excuse a little statistical laxity.
Conclusions
In general, statistics is fairly intuitive and cases that are difficult to conceptualise are rare. In general, a questioning reader must:
- Find out who is presenting the data, and what they are trying to achieve.
- If possible, find out the sample methodology – whether the data comes from a suitably representative sample of the population being measured, and whether any testing is applied in a fair manner. Are fair comparisons used, and is the right question being asked?
- Question any averages or percentages and think about how extreme the statistics really are, and what you would expect. In particular, don’t assume that mean values are typical of the data.
Statistics is a powerful and useful tool in the right hands, and we need to give people the ability to understand it. We also need to ensure that some basic education in statistics, particularly in relation to interpreting advertising, is something that every pupil receives at school. At the very least, until journalists, the marketing industry, and the people who regulate them learn some statistics and, more importantly, how to present them, the world won’t be buying the best skin cream and pet food for their cats, all of whom have an above average number of ears.

References
- DWP (2006) Households Below Average Income (HBAI) 1994/95-2004/05. London, UK: Department for Work and Pensions
- This article first appeared in Plus, a free online magazine opening a window on the world of mathematics: http://plus.maths.org. ‘Damn lies’ was a runner-up in the general public category of the Plus new writers award in 2006.
Review
The article presents a humorous view of how statistics are misused in everyday life. It would be comprehensible for teachers, students and general readers all over the world. In school, it could be used as an introduction to statistics and probability, to encourage pupils to think about how statistics and probabilities are used and misused.
I particularly like the hilarious headings and humour in the article – sometimes obvious, sometimes less so.
Marco Nicolini, Italy





