Przeklęte kłamstwa Understand article
Tłumaczenie Małgorzata Szmigielska. Czy masz ponadprzeciętną liczbę uszu? Czy zarabiasz poniżej średniej? Kiedy jest następny autobus? Ben Parker próbuje przekonać nas do wartości statystyki – poprawnie stosowanej.

Zdjęcie dzięki uprzejmości Lisa
Kyle Young/iStockphoto
O ile nie jest pewne, czy przekonanie o tym, że istnieją trzy rodzaje kłamstwa – „Kłamstwa, przeklęte kłamstwa i statystyki” wyraził po raz pierwszy Mark Twain czy Benjamin Disraeli, o tyle pewne jest, że nie straciło ono na popularności. Statystycy to manipulanci i oszuści. Zaśmiecają nasze głowy kłamliwymi i niemającymi znaczenia danymi, chcąc skłonić nas do zagłosowania na wybraną partię polityczną, używania jednego, w oczywisty sposób skutecznego kremu albo kupowania ulubionego przez ich koty pokarmu. Najwyższy już czas, żebym, jako statystyk, obalił kilka mitów.
Dokładnie 96,4% współczesnego świata obraca się wokół statystyk. I chociaż czasem wypadają one naprawdę słabo, mam nadzieję przekonać wszystkich czytelników, że zasadniczo wina leży po stronie sposobu ich przedstawiania.
Co uchodzi statystykom
Mógłbym się założyć, że ty, drogi czytelniku, masz ponadprzeciętną liczbę uszu. Dlaczego? Załóżmy, że spośród 6 miliardów osób tłumnie zamieszkujących ziemski glob, 99% ma jedną parę uszu. Nielicznymi wyjątkami będą ci, którzy w wyniku wypadku albo wrodzonej wady, mają jedno ucho albo żadnego. Z tego co wiem, nie ma ludzi z trojgiem uszu (Kapitan Kirk to niestety postać fikcyjna, ale w istocie miał troje uszu – lewe, prawe i przednie). Licząc więc średnią (liczbę uszu całej ludzkości dzieląc przez liczbę osób) otrzymujemy działanie:
Trochę poniżej 12 miliardów/6 miliardów
którego wynik to niecałe dwa. Oznacza to, że skoro większość z nas ma dwoje uszu, każdy ma troszkę więcej niż wynosi średnia. W większości przypadków zatem, wygrałbym mój zakład.
Przekaz pośredni?
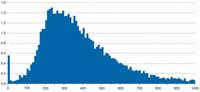
dochodów w gospodarstwie
domowym w latach
2004/2005 – liczba osób (w
milionach), Wielka Brytania.
Kliknij na obrazek aby
powiększyć.
Dane z: Households Below
Average Income (HBAI)
1994/95-2004/05,
Department for Work and
Pensions (Departament Pracy i
Emerytur).
Powyższy rachunek jest oczywiście jedynie dowodem pedanterii statystyka, ale podać można mnóstwo bardziej poważnych przykładów. Statystyki dotyczące średnich dochodów stanowią stały element debat politycznych. Zdecydowanie za często prasa donosi o alarmująco niskich zarobkach wśród obywateli, winą za nie obarczając rządzących, poprzednie rządy, Unię Europejską albo plamy na słońcu.
Według brytyjskiego Departamentu Pracy i Emerytur (Department for Work and Pensions) (zob. wykres powyżej), rozkład zarobków kształtuje się w ten sposób, że względnie niewielka liczba obywateli zarabia naprawdę duże sumy (do tej grupy statystycy niestety się nie zaliczają). Oznacza to, że średni dochód, według Departamentu wynoszący 427 funtów tygodniowo w bezdzietnym małżeństwie (DWP, 2006), jest tak naprawdę znacznie wyższy niż zarobek większości obywateli – analogicznie do naszego wcześniejszego rachunku liczby uszu. Garstka osób wyjątkowych, czy to ze względu na posiadaną liczbę uszu, czy uzyskiwane dochody, wypacza rachunek średniej odpowiadającej rzeczywistej sytuacji większości z nas.
Szybko się oczywiście zorientowano, że ta powszechnie używana średnia, zwana średnią arytmetyczną, liczona poprzez dodawanie danych wartości i dzielenie otrzymanej sumy przez liczbę składników, może zostać błędnie zinterpretowana. Dlatego zamiast średniej często stosuje się medianę. Jeśli wszystkich obywateli Wielkiej Brytanii ustawimy w szeregu uporządkowanym według ich zarobków, mediana będzie równa zarobkom osoby stojącej w środku szeregu. Wartość mediany, w tym przypadku wynosząca około 349 funtów, często stanowi bardziej rzeczywiste odzwierciedlenie tego, co można uznać za przeciętną.
W końcu udało nam się dojść do zdroworozsądkowych wniosków. Czy możemy się zatem spodziewać, że wszyscy zrozumieją ten podstawowy problem związany z obliczaniem średniej? Co by nie mówić, zadanie dobrego dziennikarza polega na przekazywaniu prawdziwych informacji w przystępny dla odbiorcy sposób.
Niestety czasem bywa tak, że wierność faktom i właściwa interpretacja danych ani dziennikarzom, ani politykom nie przysparzają popularności.
Likwidując zmarszczki

0,2 tego użytkownika.
Zdjęcie dzięki uprzejmości Al
Wekelo /iStockphoto
Jeszcze gorsi od dziennikarzy – nieupadając jednak tak nisko jak politycy – są twórcy reklam. W ukazującej się od niedawna w telewizji reklamie kremu przeciwzmarszczkowego możemy usłyszeć, że spośród 134 stosujących go uczestników ankiety, 8 na 10 jest zadowolonych z efektów. Być może da się wybaczyć niewielki rozmiar badania, a nawet zaokrągloną liczbę (134 x 8/10 = 107,2), z której wynika, że o wypróbowanie kremu poproszono 0,2 osoby. Kluczowe jednak pozostaje pytanie, w jaki sposób przeprowadzono to badanie.
Wydaje się, że zasadność pytania 134 użytkowników danego produktu, czy są z niego zadowoleni, jest wątpliwa – osoby, które z własnej woli kupiły daną rzecz i jej używają być może nie stanowią najwłaściwszej próby. Dlaczego ktokolwiek miałby kupować coś, z czego nie jest zadowolony? W badaniach tego typu, przeprowadzanych metodą naukową, należałoby porównać działanie reklamowanego kremu z kremem innej marki albo z placebo i sprawdzić, czy losowo wybrana grupa osób ocenia je pozytywnie.
Nie ma nic złego w reklamie jako takiej; filozofia uważa ją za podstawę silnej demokracji. W porządku, jeśli twórcy reklam informują nas o swoich produktach i podkreślają ich zalety. Nie do zaakceptowania jest jednak nadawanie marketingowi naukowej otoczki – dane statystyczne „8 na 10”, choć sprytnie ukrywające zastosowaną metodę pomiaru, nie mają kompletnie znaczenia. Są takim samym pustosłowiem, jak informacja, że „maksymalna prędkość samochodu wynosi 800 kilometrów na godzinę” bez wyjaśnienia, w jakich specyficznych okolicznościach ta prędkość jest osiągalna. Stosowanie takich fałszywych metod w reklamach to prosta droga do kłamstwa.
Trzy w jednej chwili
Może to niesprawiedliwe winić tych, którzy są odpowiedzialni za przekaz informacji zamiast samych ich twórców – statystyków. Czasami statystyka podejmuje się naprawdę trudnych, nieintuicyjnych tematów, które bardzo ciężko wyjaśnić. Załóżmy, że stoisz na przystanku i czekasz na autobus. Patrzysz na rozkład, z którego wynika (o ile nie został zniszczony), że w ciągu godziny kursuje pięć autobusów. Jak długo będziesz musiał czekać?
Logika podpowiada, że jeśli jest 5 autobusów na godzinę, to znaczy, że kursują średnio co 12 minut. Zatem zakładając, że zjawiasz się na przystanku w jakiejkolwiek chwili podczas tej przerwy, będziesz musiał poczekać średnio 6 minut. Słuszne rozumowanie, na ogół, niestety, błędne.
Wiadomo, że autobusy nie kursują regularnie co do minuty. Nawet jeśli punktualnie wyjadą z zajezdni, po drodze w różnych okolicznościach może dojść do opóźnienia. Trzeba zatem założyć, że rzeczywiste pory przyjazdów różnią się nieznacznie od tego, co jest napisane w rozkładzie. Możemy przyjąć różne założenia, na przykład, że autobusy kursują zgodnie z rozkładem wykładniczym. Ale ważne jest tutaj to, że nie kursują one regularnie co do minuty. Załóżmy więc, że zjawiamy się na przystanku w przypadkowym czasie. Jak długo będziemy czekać na autobus?
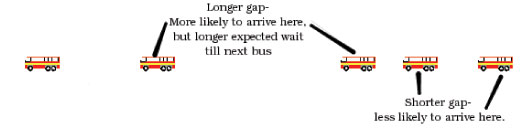
Zdjęcie dzięki uprzejmości Ben Parker
Kiedy przychodzimy na przystanek, mamy większe prawdopodobieństwo trafienia na długą przerwę – długa przerwa zabiera więcej czasu niż krótka przerwa, więc bardziej prawdopodobne jest, że kiedy przyjdziemy o przypadkowej porze, trafimy na tę pierwszą. Załóżmy więc, że trafiliśmy na długą przerwę. Wiemy, że będzie trwała dłużej niż 12 minut (nadal zakładamy, że jest 5 autobusów w ciągu godziny), więc średni czas oczekiwania wyniesie więcej niż 6 minut.
Zjawisko to nosi nazwę paradoksu inspekcji. Trudno je pojąć, ale funkcjonuje w rzeczywistości i jest wykorzystywane w planowaniu ruchu komunikacyjnego oraz w badaniach operacyjnych, na przykład zajmujących się analizowaniem procesu powstawania kolejek i opracowywaniem optymalnych (i tak później nie branych pod uwagę) metod organizacji obsługi.
Czy zatem błędne jest podawanie informacji, że autobusy kursują co 12 minut? Tak myślę, chociaż trudno byłoby przekazać wszystkie drastyczne szczegóły dotyczące paradoksu inspekcji. Chyba więc w tym przypadku możemy wybaczyć tę drobną statystyczną nieścisłość.
Wnioski
Ogólnie rzecz biorąc, statystyka jest dosyć intuicyjną dziedziną, a przykłady trudne do wyobrażenia należą do rzadkości. Dociekliwy odbiorca powinien zatem:
- Sprawdzić, kto przedstawia konkretne dane i w jakim celu.
- Jeśli to możliwe, sprawdzić metodologię – czy pomiar został przeprowadzony na reprezentatywnej próbie i czy był rzetelny. Czy zastosowano uczciwe porównania i zadano właściwe pytania?
- Sceptycznie podchodzić do tego, co przedstawia się jako wartości średnie i procentowe. Nie należy zakładać, że średnia odzwierciedla to, co uznalibyśmy za typowe w danej sytuacji.
Statystyka to potężne narzędzie. To też narzędzie pożyteczne, jeśli tylko znajduje się w odpowiednich rękach – dlatego trzeba dać ludziom szansę je zrozumieć. Trzeba również zapewnić podstawową edukacje w zakresie statystyki, co wydaje się szczególnie ważne w odniesieniu do sposobu interpretowania reklam. Przynajmniej dopóki dziennikarze i marketingowcy nie dowiedzą się trochę więcej o statystykach i, co ważniejsze, o sposobie ich przedstawiania, nie będziemy kupowali najlepszego kremu do twarzy i najlepszego pokarmu dla naszych kotów.

References
- DWP (2006) Households Below Average Income (HBAI) 1994/95-2004/05. London, UK: Department for Work and Pensions
- Artykuł ten po raz pierwszy opublikowano w Plus, darmowym czasopiśmie internetowym – http://plus.maths.org. „Przeklęte kłamstwa” były liderem rankingu czytelników do nagrody dla nowego autora w 2006 roku, przyznawanej przez czasopismo.
Review
Artykuł ten w zabawny sposób przedstawia znaną z codziennego życia praktykę nadużywania statystyk. Jest napisany w sposób, który umożliwia zrozumienie tematu przez nauczycieli, uczniów i szeroki krąg czytelników. W szkole można go wykorzystać jako wstęp do statystyki i rachunku prawdopodobieństwa, tak aby zachęcić uczniów do zastanowienia się, w jaki sposób statystyki są używane i nadużywane.
Szczególnie podobały mi się zabawne nagłówki – niektóre łatwe do zrozumienie, inne niekoniecznie.
Marco Nicolini, Włochy





