The new definition of crystals – or how to win a Nobel Prize Understand article
Why is symmetry so central to the understanding of crystals? And why did ‘forbidden’ symmetry change the definition of crystals themselves?

Schellhase; image source:
Wikimedia Commons
Studying crystalline materials is one of the most powerful analytical techniques available to scientists. If it is possible to grow a single crystal of a salt, molecule, protein or even a whole virus, then it is usually possible to identify not only its connectivity (what atoms are bonded to what), but also its bond lengths, bond angles and molecular conformation (what shape a flexible molecule adopts). From the study of protein crystals, it is often possible to elucidate how that protein works in the body and where its active sites are.
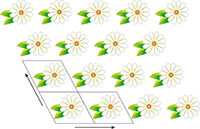
illustrating translational
symmetry in two dimensions.
The parallelograms indicate
the repeating unit. Click on
image to enlarge
Image courtesy of Mairi
Haddow
Crystals are inherently beautiful, thanks largely to their symmetry. Conventionally, all crystals were thought to have one property in common: translational symmetry in three dimensions. Indeed, this is how crystals were originally defined – as materials in which the constituent atoms, molecules, or ions are packed in a regularly ordered, repeating three-dimensional pattern. Translational symmetry is best illustrated in two dimensions by thinking about patterned wallpaper, which usually has this property – if hung properly. This means that we can draw a parallelogram (tile) containing a certain pattern, and by stacking the tile in two directions, derive the wallpaper pattern (figure 1).
In a similar way, we can derive a 3D crystal structure from a ‘box’ of atoms, by repeating the box along the x, y, and z axes. The repeating box is known as the unit cell (figure 2).
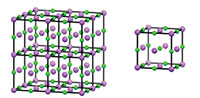
Click on image to enlarge
Image courtesy of Mairi Haddow

the atomic structure of
quasi- periodic crystals at a
meeting at the National
Institute of Standards and
Technology, USA, in 1985 –
just months after he
published his discovery
Image courtesy of Phillip
Westcott, National Institute of
Standards and Technology
Symmetry in crystals and quasi-periodicity
Crystals that have such translational symmetry in three dimensions are formally referred to as periodic crystals because the structures have a pattern that repeats at a certain distance or period. In 2011, however, the Nobel Prize in Chemistry was awarded to Dan Shechtman for his discovery of quasi-periodic crystals. These crystals are not periodic – they do not possess translational symmetry – but still have local order. They have the same repeating unit at different points in the crystal, but not at periodic intervals. The recent recognition of this work is a triumph of Shechtmann’s perseverance over the ridicule that he received when he first published his work (Shechtman et al., 1984). So why was this idea so contentious? Because these crystals seemed to have symmetries that are forbidden in periodic systems.
In addition to translational symmetry, most periodic crystal structures have additional symmetry, such as mirror symmetry. For example, by looking at the unit cell of sodium chloride, we can see that each half is the mirror image of the other (figure 3; see also figure 4).
Rotational symmetry is also possible. This means that if we take an object and rotate it around a central point by a certain number of degrees, it will look the same (figure 4).
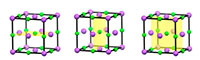
Click on image to enlarge
Image courtesy of Mairi Haddow

Click on image to enlarge
Public domain image (recycling symbol); other images courtesy of Mairi Haddow
Click on image to enlarge
Image courtesy of Mairi Haddow
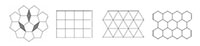
When a pattern or crystal has translational symmetry and is periodic, two-fold, three-fold, four-fold and six-fold rotational symmetries are all possible, but five-fold, or indeed seven-fold or higher symmetry, is not. This is because triangles, rectangles, squares and hexagons may all be packed in 2D space without leaving any space in between. In contrast, pentagons, heptagons and higher polygons may not (figure 5).
How are crystals analysed?
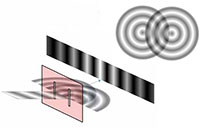
experiment, showing the
interference of light passing
through a diffraction grating.
Click on image to enlarge
Image courtesy of Mairi
Haddow
Many students will have performed Young’s famous double-slit experiment at school, in which a laser is shone through two slits in a diffraction grating, the spacing between which is comparable to the wavelength of the laser light. An interference pattern can be seen, caused by constructive and deconstructive interference of the waves diffracted by the slits (figure 6).
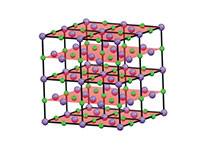
sodium chloride that act
similarly to slits in a
diffraction grating
Click on image to enlarge
Image courtesy of Mairi
Haddow
Crystals are studied using a technique known as X-ray diffraction, the theory of which was developed extensively in 1913 by William Henry Bragg and his son William Lawrence Bragg, who were jointly awarded the Nobel Prize in Physics in 1915 for their work. In a diffraction experiment, crystals act as a complex diffraction grating, where the ‘slits’ are layers of atoms in the crystal (figure 7).
For diffraction to occur, the wavelength of the radiation interacting with the crystal must be comparable to the distance between the atoms.
Commonly in laboratories, the radiation will be X-rays (which are scattered by the electrons in atoms), but there are other possibilities, such as electrons or neutronsw1.
The crystal is mounted in an X-ray beam of a selected wavelength, and the diffraction pattern is measured as the crystal is rotated. For layers of atoms positioned at an angle θ to the X-ray beam, scattered X-rays will be in phase (i.e. have constructive interference) if and only if the difference between the path lengths of two scattered X-rays is equal to a whole number of wavelengths, resulting in a measurable diffraction peak. This is known as Bragg’s law, and the derivation is illustrated in figure 8.
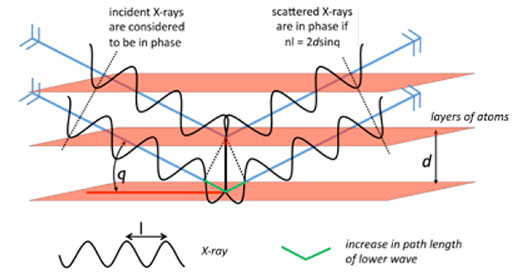
Image courtesy of Mairi Haddow

pattern from a conventional
crystal at one particular
angle. Each bright spot
(reflection) represents
constructive interference
from a different layer of
atoms. (The shape on the
right is the shadow of the
beam stop, a metal shield
which absorbs the
unscattered X-ray beam)
Image courtesy of Mairi
Haddow
As the crystal is rotated, different layers of atoms will satisfy Bragg’s law and produce constructive interference. This results in a diffraction peak with an intensity related to the number and type of atoms in the layer, for example as shown in figure 9. A typical diffraction experiment will measure thousands to millions of reflections, and by careful analysis can be used to figure out the exact structure of the crystal.
The diffraction pattern produced by a crystal also has symmetry and this is related to the symmetry of the crystal. The diffraction patterns of quasi-periodic crystals have symmetry that is forbidden in periodic crystals, such as five- or 10-fold rotation (figure 10).
The structures of these unusual crystals are related to Penrose tilings (figure 11). These are structures that possess local symmetry, but not translational symmetry.

Images courtesy of Mairi Haddow (right and left images); central image courtesy of Materialscientist; image source: Wikimedia Commons

may possess five-fold
rotational symmetry (top)
but these objects may not be
combined into a periodic
system. This occurs, for
example, in Penrose tiling
(bottom), in which instances
of local five-fold symmetry
may be found, but which
does not have translational
symmetry. Click on image to
enlarge
Image courtesy of Mairi
Haddow
Research in this area led to a change in the definition of a crystal by the International Union of Crystallography in 1991. Crystals now no longer need to have translational symmetry: a material is a crystal if it has a sharp diffraction pattern, which quasi-periodic crystals certainly do.
However, it’s unlikely that the school curriculum will be changed any time soon to reflect this new definition. Very few of these quasi-periodic materials have yet been discovered, and the first natural quasi-periodic crystal – icosahedrite (Al63Cu24Fe13), a mineral that is probably of meteoritic origin and was found in the Khatyrka river in eastern Russia – was discovered only in 2009 (Bindi L et al., 2009). Although more examples have been created since then, and quasi-crystals are now known to exist in many metallic alloys and some polymers, the crystals that school students grow in the lab are unlikely to be anything but periodic, and aside from their unusual and interesting properties, quasi-crystals have no real applications – yet.
References
- Bindi L et al. (2009) Natural Quasicrystals. Science 324(5932): 1306-1309. doi: 10.1126/science.1170827
- Shechtman D et al. (1984) Metallic phase with long-range orientational order and no translational symmetry. Physical Review Letters, 53(20): 1951-1953. doi: 10.1103/PhysRevLett.53.1951
Web References
- w1 – Diffraction analysis is possible not only with X-rays, but also with neutrons and electrons. This is exemplified by three of the members of EIROforum, the publisher of Science in School.
- The European Synchrotron Radiation Facility uses the diffraction patterns of high-energy X-rays to analyse materials. The experiments carried out at ESRF have applications not only in materials science, but also in biology, medicine, physics, chemistry, environmental science and even palaeontology and cultural heritage.
- The Institut Laue-Langevin operates the most intense steady neutron source in the world. Diffraction studies of the neutron beams are used in research into condensed matter physics, chemistry, biology, nuclear physics and materials science.
- The European X-ray Free Electron Laser, due to start operation in 2015, will use X-ray flashes to examine samples. The basic idea behind a typical experiment is simple: illuminate a sample by intense X-ray flashes and count the photons that are scattered from the sample in different directions. The result is a diffraction pattern.
Resources
- Cornuéjols D (2009) Biological crystals: at the interface between physics, chemistry and biology. Science in School 11: 70-76.
- To learn how to grow your own protein crystals at school, see:
- Blattmann B, Sticher P (2009) Growing crystals from protein. Science in School 11: 30-36.
- More information about Dan Shechtman and his discovery.
- Howes L (2011) Quasicrystals scoop prize. Chemistry World 8(11): 38-41.
- For an interview with mathematician and symmetry researcher Marcus de Sautoy, see:
- Hayes E (2012) Finding maths where you least expect it: interview with Marcus du Sautoy. Science in School 23: 6-11.
Review
As the author writes, “crystals are inherently beautiful,” but students often regard crystallography as a difficult and boring subject. For these students and for their teachers, Mairi Haddow’s article is a valuable resource to look at crystals with a new and inspiring approach. In this enjoyable article, the topic is explained in clear and precise language, together with beautiful and impressive pictures (for example the one about wallpaper and translational symmetry).
The article could be used in school within chemistry (solid structures), physics (diffraction, waves, atomic structure), earth science (mineralogy, crystallography), and maths (symmetry) curricula. These subjects, with the addition of art history (tiling), offer different interdisciplinary opportunities.
Suitable comprehension questions include:
- From the article you can deduce that it is possible to grow a crystal of:
- A salt
- A molecule
- A virus
- A bacterium
- With which of the following can diffraction analysis of crystals NOT be performed?
- X-rays
- Radio waves
- Neutrons
- Free electron laser
- With which of the following types of tiles is it possible to completely cover a 2D surface?
- Triangles, squares, pentagons, and hexagons
- Triangles, rectangles and heptagons
- Triangles, squares, rectangles and hexagons
- Squares, rectangles and pentagons
Giulia Realdon, Italy
