La nueva definición de cristal o cómo ganar un Premio Nobel Understand article
Traducido por Julia Martínez Beamonte. ¿Por qué la simetría resulta tan importante para comprender los cristales? y ¿cómo es que la simetría “prohibida” cambió la definición de los mismos cristales?

Schellhase; Origen de la
imagen: Wikimedia Commons
El estudio de los materiales cristalinos es una de las técnicas analíticas más poderosas al alcance de los científicos. Si se puede hacer crecer un cristal único de sal, de una molécula, de una proteína o incluso de un virus completo, entonces será posible identificar no solo su conectividad (qué átomos están enlazados a qué), sino también sus distancias y ángulos de enlace así como su forma molecular (la forma que adopta una molécula flexible). A partir del estudio de los cristales de proteínas, a menudo es posible dilucidar cómo funcionan las proteínas en el cuerpo y dónde están sus centros activos.
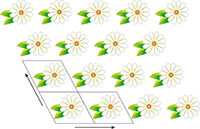
muestra la simetría
traslacional en dos
dimensiones. Los
paralelogramos indican el
motivo repetido. Haga clic en
la imagen para ampliarla
Imagen cortesía de Mairi
Haddow
Los cristales son intrínsecamente hermosos, gracias en gran medida a su simetría. Antes se pensaba que todos los cristales tenían una propiedad en común, la simetría traslacional en tres dimensiones. De hecho, los cristales se definían originalmente como materiales en los que los átomos, las moléculas o los iones formaban un motivo tridimensional repetido y ordenado de manera regular. La simetría traslacional se visualiza mejor en dos dimensiones al imaginar un papel pintado estampado, que normalmente tiene esta propiedad siempre que se coloque adecuadamente. Esto significa que podemos dibujar un paralelogramo (mosaico) que contenga un determinado motivo y, mediante la colocación de los mosaicos en dos direcciones, generar el motivo estampado en el papel (figura 1).
De manera análoga, se puede obtener la estructura cristalina en 3D de una “caja” de átomos, mediante la repetición de la caja a lo largo de los ejes X, Y, Z. Esta caja que se repite, se llama celda unidad (figura 2).
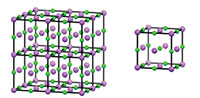
Haga clic en la imagen para ampliarla
Imagen cortesía de Mairi Haddow

estructura atómica de los
cristales cuasiperiódicos en
una reunión de 1985 en el
Instituto Nacional de Normas
y Tecnología de EE.UU., unos
meses antes de publicar su
descubrimiento
Imagen cortesía de Phillip
Westcott, Instituto Nacional de
Normas y Tecnología
La simetría en los cristales y la cuasiperiodicidad
Los cristales con simetría traslacional en tres dimensiones se conocen formalmente como cristales periódicos porque sus estructuras presentan un motivo que se repite a una determinada distancia o periodo. En 2011, sin embargo, Dan Shechtman recibió el Premio Nobel de Química por su descubrimiento de los cristales cuasiperiódicos. Estos cristales son aperiódicos (carecen de simetría traslacional) pero aún así tienen orden de corto alcance. Es decir, poseen la misma unidad que se repite en diferentes puntos del cristal, pero no a intervalos periódicos. El reciente reconocimiento de la investigación de Shechtman supone el triunfo de su perseverancia frente al menosprecio que sufrió cuando se publicó su trabajo (Shechtman et al., 1984). ¿Por qué, entonces, su idea resultaba tan polémica? Porque estos cristales parecían tener simetrías que están prohibidas en los sistemas periódicos.
Además de contar con simetría traslacional, la mayoría de las estructuras cristalinas periódicas presentan una simetría adicional: la simetría especular. Por ejemplo, si observamos la celda unidad del cloruro sódico podemos ver que cada una de sus mitades es la imagen especular de la otra (figura 3; ver también la figura 4).
Estos cristales también pueden presentar simetría de rotación. Esto significa que si rotamos un objeto un cierto número de grados alrededor de un punto central, mantendrá la misma apariencia (figura 4).
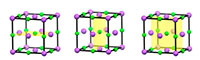
Haga clic en la imagen para ampliarla
Imagen cortesía de Mairi Haddow

Haga clic en la imagen para ampliarla
Imagen de dominio público (símbolo del reciclaje); las demás imágenes cortesía de Mairi Haddow
Haga clic en la imagen para ampliarla
Imagen cortesía de Mairi Haddow
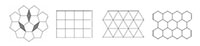
Cuando un motivo o un cristal posee simetría traslacional y es periódico, puede tener simetría rotacional de segundo, de tercer, de cuarto y de sexto orden. Por el contrario, no puede tener simetría rotacional de quinto o de séptimo orden o mayor. Esto se debe a que los triángulos, los rectángulos, los cuadrados y los hexágonos pueden cubrir completamente una superficie bidimensional sin dejar ningún hueco libre. En cambio, para los pentágonos, los heptágonos y otros polígonos con mayor número de lados es imposible rellenar todo el espacio (figura 5).
¿Cómo se analizan los cristales?
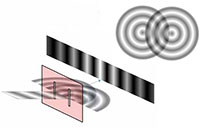
experimento de Young
muestra la interferencia de
la luz al atravesar el
enrejado de difracción.
Haga clic sobre la imagen
para ampliarla
Imagen cortesía de Mairi
Haddow
Muchos estudiantes habrán realizado en la escuela el famoso experimento de Young sobre la doble rendija. En este experimento se utiliza un enrejado de difracción en el que un haz láser atraviesa dos rendijas separadas entre sí por una distancia comparable a la longitud de onda de la luz láser. La luz que sale de las dos rendijas produce un patrón de interferencia, que se forma como consecuencia de las interferencias constructivas y destructivas de las ondas difractadas por las rendijas (figura 6).
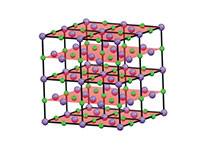
átomos en el cloruro sódico
actúan de manera similar a
las rendijas en un enrejado
de difracción. Haga clic sobre
la imagen para ampliarla
Imagen cortesía de Mairi
Haddow
Los cristales se estudian utilizando una técnica conocida como difracción de rayos X. William Henry Bragg y su hijo William Lawrence Bragg desarrollaron en profundidad esta teoría en 1913 y obtuvieron conjuntamente el Premio Nobel de Física por su trabajo en 1915. En un experimento de difracción, los cristales actúan como un enrejado de difracción complejo donde los rendijas son capas de átomos en el cristal (figura 7).
Para que se produzca la difracción, la longitud de onda de la radiación que interactúa con el cristal debe ser equiparable a la distancia entre los átomos.
Normalmente en laboratorio la radiación utilizada será de rayos X (que son dispersados por los electrones en los átomos), pero hay otras posibilidades, como los electrones o los neutronesw1.
El haz de rayos X incide en el cristal a una longitud de onda seleccionada y el patrón de la difracción se mide a medida que el cristal gira. Los rayos X dispersados estarán en fase (es decir, tendrán una interferencia constructiva) cuando las capas de átomos estén situadas en un ángulo θ respecto al haz de rayos X, si y solo si la diferencia entre la longitud de los recorridos de los dos rayos X dispersados es igual al número entero de longitudes de onda, lo que resulta en un pico de difracción medible. Esto se conoce como la ley de Bragg y la deducción se muestra en la figura 8.
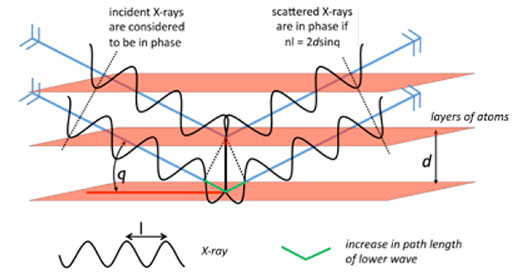
Imagen cortesía de Mairi Haddow

difracción de un cristal
convencional con un ángulo
específico. Cada uno de los
puntos brillantes (reflejos)
representa una interferencia
constructiva de una capa
distinta de átomos. (La
imagen de la derecha es la
sombra del “beam stop”, una
placa de metal que absorbe
el haz de rayos X no
dispersado)
Imagen cortesía de Mairi
Haddow
A medida que el cristal gira, las diferentes capas de átomos cumplirán la ley de Bragg y producirán una interferencia constructiva. Se obtiene entonces un pico de difracción con una intensidad relacionada con el número y tipo de átomos de la capa, como se muestra, por ejemplo, en la figura 9. Un experimento de difracción típico medirá entre miles y millones de reflexiones y mediante un cuidadoso análisis se puede utilizar para explicar la estructura exacta del cristal.
El patrón de difracción producido por un cristal también tiene simetría y está relacionado con la simetría del cristal. Los patrones de difracción de los cristales cuasiperiódicos tienen una simetría que está prohibida en los cristales periódicos, como las simetrías rotacionales de quinto o décimo orden (figura 10).
Las estructuras de estos cristales singulares están relacionadas con las teselaciones de Penrose (figura 11). Estas estructuras se caracterizan por presentar simetría local, pero no simetría traslacional.

Imágenes cortesía de Mairi Haddow (imágenes derecha e izquierda); imagen central cortesía de Materialscientist; Origen de la imagen: Wikimedia Commons

puede poseer una simetría
rotacional de quinto orden
(arriba) pero estos objetos
no pueden combinarse en
un sistema periódico. Esto
ocurre, por ejemplo, en las
teselaciones de Penrose
(abajo), en las que se
pueden encontrar simetrías
locales de orden cinco que
carecen de simetría
traslacional. Haga clic sobre
la imagen para ampliarla
Imagen cortesía de Mairi
Haddow
En 1991 la Unión Internacional de Cristalografía modificó la definición de cristal a raíz de las investigaciones en este campo. Actualmente, ya no es necesario que un cristal tenga simetría traslacional: un material se considera un cristal si tiene un patrón de difracción nítido, como el de los cristales cuasiperiódicos.
Sin embargo, no es probable que los planes de estudios cambien a corto plazo para reflejar esta nueva definición. Hasta la fecha se han descubierto muy pocos cristales cuasiperiódicos. El primer cristal natural cuasiperiódico es la icosaedrita (Al63Cu24Fe13), que se encontró en 1991 en el río Khatyrka al este de Rusia y que probablemente es de origen meteorítico (Bindi L et al., 2009). Aunque se han creado más cuasicristales artificiales desde entonces, y ahora se conoce su existencia en muchas aleaciones metálicas y en algunos polímeros, es poco probable que los cristales que los estudiantes hacen crecer en el laboratorio no sean periódicos. Al margen de sus interesantes propiedades singulares, los cuasicristales no tienen ninguna aplicación práctica…por el momento.
References
- Bindi L et al. (2009) Natural Quasicrystals. Science 324(5932): 1306-1309. doi: 10.1126/science.1170827
- Shechtman D et al. (1984) Metallic phase with long-range orientational order and no translational symmetry. Physical Review Letters, 53(20): 1951-1953. doi: 10.1103/PhysRevLett.53.1951
Web References
- w1 – El análisis por difracción no solo es posible con rayos X, sino también con neutrones y electrones. Tres de los miembros de EIROforum, la editorial de Science in School, ejemplifican estas difracciones.
-
El laboratorio Europeo de Radiación Sincrotón (ESRF por sus siglas en inglés) utiliza los patrones de difracción de rayos X de alta energía para analizar materiales. Los experimentos llevados a cabo en el ESRF tienen aplicaciones tanto para la ciencia de los materiales como en biología, medicina, física, química, ciencias medioambientales e incluso en paleontología y patrimonio cultural.
-
El Instituto Laue-Langevin está a cargo de la fuente de neutrones continua más intensa del mundo. Los estudios de difracción de los haces de neutrones se utilizan en la investigación en física de la materia condensada, química, biología, física nuclear y ciencia de los materiales.
-
La Instalación Europea de Láser de Electrones Libres de Rayos X (European XFEL por sus siglas en inglés) dse pondrá en funcionamiento en 2015 y utilizará destellos de rayos X para examinar muestras. La idea básica detrás de uno de estos experimentos es simple: iluminar la muestra mediante destellos intensos de rayos X y contar los fotones que se dispersan de la muestra en diferentes direcciones. El resultado es un patrón de difracción.
-
Resources
- Cornuéjols D (2009) Biological crystals: at the interface between physics, chemistry and biology. Science in School 11: 70-76.
- Para aprender a cristalizar proteínas en la escuela, ver:
-
Blattmann B, Sticher P (2009) Growing crystals from protein. Science in School 11: 30-36.
-
- Más información sobre Dan Shechtman y su descubrimiento.
- Howes L (2011) Quasicrystals scoop prize. Chemistry World 8(11): 38-41.
- Una entrevista con el matemático e investigador de simetría Marcus du Sautoy, ver:
-
Hayes E (2012) Las matemáticas se encuentran donde menos te lo esperas: entrevista con Marcus du Sautoy. Science in School 23.
-
Review
Tal y como señala la autora, “los cristales son intrínsecamente hermosos”, pero los estudiantes a veces consideran que la cristalografía es una asignatura difícil y aburrida. Para estos estudiantes y para sus profesores, el artículo de Mairi Haddow representa un valioso recurso para observar los cristales con un enfoque nuevo e inspirador. En este entretenido artículo, el tema se aborda con un lenguaje claro y preciso, además de contar con unas preciosas e impresionantes imágenes (como, por ejemplo, la del papel pintado y la simetría traslacional).
Este artículo se podría utilizar en diferentes asignaturas de enseñanza media y superior: química (estructuras sólidas), física (difracción, ondas y estructura atómica), ciencias de la tierra (cristalografía y mineralogía) y matemáticas (simetría). Estas asignaturas, junto con historia del arte (teselas), ofrecen diversas oportunidades para un enfoque interdisciplinar.
Preguntas adecuadas para comprobar la comprensión del artículo:
- A partir del artículo puedes deducir si es posible hacer crecer un cristal de:
- Sal
- Una molécula
- Un virus
- Una bacteria
- ¿Con cuál de las siguientes técnicas NO puede realizarse un análisis de difracción de cristales?
- Rayos X
- Ondas de radio
- Neutrones
- Láser de electrones libres
- ¿Con cuál de los siguientes tipos de teselas es posible cubrir completamente una superficie en 2D?
- Triángulos, cuadrados, pentágonos y hexágonos
- Triángulos, rectángulos y heptágonos
- Triángulos, cuadrados, rectángulos y hexágonos
- Cuadrados, rectángulos y pentágonos
Giulia Realdon, Italia





