Symmetry rules Understand article
Everyone knows what symmetry is. In this article, though, Mario Livio from the Space Telescope Science Institute, Baltimore, USA, explains how not only shapes, but also laws of nature, can be symmetrical.
Everybody will recognize the inkblot below left as being symmetrical, but few know that the figure below right is also considered symmetrical in the precise mathematical sense. So, what is symmetry, really? And why has this concept become so pivotal that many scientists believe it to be the basis of the laws of nature?


symmetrical…
When things that could have changed, don’t
Symmetry represents immunity to possible alterations — those stubborn cores of shapes, phrases, laws, or mathematical expressions that remain unchanged under certain transformations. Consider, for instance, the phrase “Madam, I’m Adam”, which is symmetrical when read back to front, letter by letter. That is, the sentence remains the same when read backwards.

symmetry
The title of the documentary, A Man, a Plan, a Canal, Panama, has the same property. Phrases with this type of symmetry are known as palindromes, and palindromes play an important role in the structure of the male-defining Y chromosome. Until 2003, genome biologists believed that, due to the fact that the Y chromosome lacks a partner (with which it could swap genes), its genetic cargo was about to dwindle away through damaging mutations. To their surprise, however, the researchers who sequenced the Y chromosome discovered that it fights destruction with palindromes. About 6 million (out of 50 million) of the chromosome’s DNA letters form palindromic sequences. These ‘mirror’ copies provide backups in the case of damaging mutations, and allow the chromosome, in some sense, to have sex with itself — strands can swap position.
For two-dimensional figures and shapes, like those drawn on a piece of paper, there are precisely four types of ‘rigid’ symmetry (when stretching and distortions are not allowed), known as: reflection, rotation, translation, and glide reflection.

under rotation
We encounter symmetry under reflection all around us — this is the familiar bilateral symmetry that characterises animals. Draw a line down the middle of a picture of a butterfly (right). Now flip it over, while keeping the central line in place. The resulting perfect overlap indicates that the butterfly remains unchanged under reflection about its central line.
Many letters of the alphabet also have this property. If you hold a sheet of paper up to a mirror with the phrase ‘MAX IT WITH MATH’ written vertically, it looks the same.
Symmetry under rotation is also very prevalent in nature. A snowflake (right) rotated through 60, 120, 180, 240, 300, or 360 degrees about an axis through its centre (perpendicular to its plane) leads to an indistinguishable configuration. A circle rotated through any angle about a central, perpendicular axis will remain unaltered.
Symmetry under translation is the type of immunity to change that is encountered in recurring, repeating motifs, such as the one in the second figure. Translation means a displacement or shift, by a certain distance, along a particular line. Many classical friezes, wallpaper designs, rows of windows in high-rise apartment buildings, and even centipedes, exhibit this type of symmetry.
Finally, the footprints generated by a left-right-left-right walk are symmetrical under glide reflection (see below). The transformation in this case consists of a translation (or glide), followed by a reflection in a line parallel to the direction of the displacement (the dotted line).

All of the symmetries discussed so far are symmetries of shape and form — ones that we can actually see with our own eyes. The symmetries underlying the fundamental laws of nature are in some sense closely related to these, but instead of focusing on form or figure they address a different question: what transformations can be performed on the world around us that would leave unchanged the laws describing all observed phenomena?
Symmetry rules
The ‘laws of nature’ collectively describe a body of rules that are supposed to explain literally everything we observe in the universe. That such a grand set of rules even exists was inconceivable before the 17th century. Only through the works of scientific giants such as Galileo Galilei (1564-1642), René Descartes (1596-1650), and in particular, Isaac Newton (1642-1727), did it become clear that a mere handful of laws could explain a wide range of phenomena. Suddenly, things as diverse as the falling of apples, tides on the beach, and the motion of the planets all fell under the umbrella of Newton’s law of gravitation.
Similarly, building on the impressive experimental results of Michael Faraday (1791-1867), the Scottish physicist James Clerk Maxwell (1831-1879) was able to explain all the classical electric, magnetic, and light phenomena with just four equations! Think about this for a moment – the entire world of electromagnetism in four equations.
The laws of nature were found to obey some of the same symmetries we have already encountered, as well as a few other, more esoteric, ones. To begin with, the laws are symmetrical under translation. The manifestation of this property is simple: whether you perform an experiment in New York or Los Angeles, at the other edge of the Milky Way or in a galaxy a billion light-years from here, you will be able to describe the results using the same laws. How do we know this to be true? Because observations of galaxies all across the universe show not only that the law of gravity is the same there as here, but also that hydrogen atoms at the edge of the observable universe obey precisely the same laws of electromagnetism and quantum mechanics as they obey here on Earth.
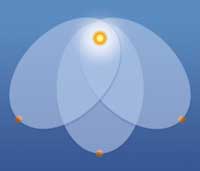
be symmetrical under
rotation, but this doesn’t
mean the orbits are
The laws of nature are also symmetrical with respect to rotation – the laws look precisely the same whether we measure directions with respect to north or the nearest coffee shop – physics has no preferred direction in space.
If it were not for this remarkable symmetry of the laws under translation and rotation, there would be no hope of ever understanding different parts of the cosmos. Furthermore, even here on Earth, if the laws were not symmetrical, experiments would have to be repeated in every laboratory across the globe.
A word of caution is needed to distinguish between symmetries of shapes and symmetries of laws. The ancient Greeks thought that the orbits of the planets around the sun were symmetrical with respect to rotation: circular. In fact, it is not the shape of the orbit, but Newton’s law of gravity that is symmetrical under rotation. This means that the orbits can be (and indeed are!) elliptical, but that the orbits can have any orientation in space (left).
In my opening paragraph, I made a statement stronger than merely saying that the laws obey certain symmetries; I said that symmetry may be the source of laws. What does this mean?
The source of natural laws
Imagine that you have never heard of snowflakes before, and someone asks you to guess the shape of one. Clearly, this is an impossible task. For all you know, the snowflake may look like a teapot, like the letter S, or like Bugs Bunny.

snowflake
Even if you are given the shape of one ray of the snowflake (right, a) and are told that this is part of its total shape, this is not much help. The snowflake could still look, for example, like the configuration right, b. If you are told, on the other hand, that the snowflake is symmetrical under rotations through 60 degrees about its centre, this information can be used very effectively. The symmetry immediately limits the possible configurations to six-cornered, twelve-cornered, eighteen-cornered, and so on, snowflakes. Assuming, based on experience, that nature would opt for the simplest, most economical solution, a six-cornered snowflake (right, c) would be a very reasonable guess. In other words, the requirement of the symmetry of the shape has guided us in the right direction.
In the same way, the requirement that the laws of nature would be symmetrical under certain transformations not only dictates the form of these laws, but also, in some cases, necessitates the existence of forces or of yet undiscovered elementary particles. Let me explain, using two interesting examples.
One of Einstein’s main goals in his explanation of general relativity was to formulate a theory in which the laws of nature would look precisely the same to all observers. That is, the laws had to be symmetrical under any change in our point of view in space and time (in physics, this is known as ‘general covariance’). An observer sitting on the back of a giant turtle should deduce the same laws as an observer on a merry-go-round or in an accelerating rocket. Indeed, if the laws are to be universal, why should they depend on whether the observer is accelerating?
Although Einstein’s symmetry requirement was certainly reasonable, it was by no means trivial. After all, a million whiplash injuries per year in the United States alone demonstrate that we feel acceleration. Every time an aeroplane hits an air pocket, we feel our stomachs leap into our throats — there appears to be an unmistakable distinction between uniform and accelerating motion. So how can the laws of nature be the same for accelerating observers, when these observers appear to experience additional forces?
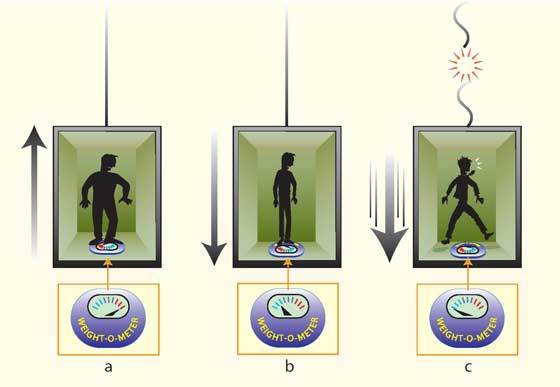
Consider the following situation. If you stand on bathroom scales inside an elevator that is accelerating upward, your feet exert a greater pressure on the scales — the scales will register a higher weight (below, a). The same would happen, however, if gravity somehow became stronger in a static elevator. An elevator accelerating downward would feel just like weaker gravity (below, b). If the elevator’s cable snapped, you and the scales would free-fall in unison, and the scales would register zero weight (below, c). Free-fall is therefore equivalent to someone miraculously switching gravity off. This led Einstein in 1907 to a ground-breaking conclusion: the force of gravity and the force resulting from acceleration are in fact one and the same. This powerful unification has been dubbed the ‘equivalence principle’, implying that acceleration and gravity are really two facets of the same force — they are equivalent.
In a lecture delivered in Kyoto in 1922, Einstein described that moment of epiphany he had in 1907: “I was sitting in the patent office in Bern when all of a sudden a thought occurred to me: if a person falls freely, he won’t feel his own weight. I was startled. This simple thought made a deep impression on me. It impelled me toward a theory of gravitation.”
The equivalence principle is really a statement of a pervasive symmetry; the laws of nature — as expressed by Einstein’s equations of general relativity — are the same in all systems, including accelerating ones. So why are there apparent differences between what is observed on a merry-go-round and in a laboratory at rest? General relativity provides a surprising answer. They are differences only in the environment, not in the laws themselves. Similarly, the directions of up and down only appear to be different on Earth because of the Earth’s gravity. The laws of nature themselves have no preferred direction (they are symmetrical under rotation); they do not distinguish between up and down. Observers on a merry-go-round, according to general relativity, feel the centrifugal force that is equivalent to gravity. The conclusion is truly electrifying: the symmetry of the laws under any change in the space-time co-ordinates necessitates the existence of gravity! This explains why symmetry is the source of forces. The requirement of symmetry leaves nature no choice: gravity must exist.
Review
Dr. Mario Livio, a Senior Astrophysicist at the Space Telescope Science Institute, gives a very interesting account of the symmetry of the laws of nature. For figures and shapes drawn on a piece of paper, there are four types of symmetries: reflection, rotation, translation, and glide reflection. How can these be applied to the laws of nature? Are the laws of nature symmetrical? And which transformations can be performed on them so that the laws remain unchanged?
Although not directly connected with curriculum material for school science, this article will surely interest all science teachers who would like to improve their understanding of the laws that govern the universe. Mathematics teachers would find this article of particular interest.
Elton Micallef, Malta
