Το μέτρο της συμμετρίας Understand article

Μετάφραση Αντώνης Γίτσας (Antonis Gitsas), Πανεπιστήμιο Ιωαννίνων, Τμήμα Φυσικής. Όλοι γνωρίζουμε τι είναι η συμμετρία. Σε αυτό το άρθρο ο Mario Livio από το Space Telescope Science…

Όλοι μπορούν να αναγνωρίσουν ότι η παρακάτω κηλίδα μελάνης είναι συμμετρική, αλλά λίγοι ξέρουν ότι το σχήμα κάτω δεξιά θεωρείται επίσης συμμετρικό υπό την αυστηρή μαθηματική έννοια. Επομένως, τι είναι, αλήθεια, η συμμετρία; Και γιατί αυτή η έννοια έχει γίνει τόσο θεμελιώδης ώστε πολλοί επιστήμονες να πιστεύουν ότι είναι η βάση των νόμων της φύσης;

Όταν τα πράγματα που θα μπορούσαν να αλλάξουν, δεν αλλάζουν

Η συμμετρία αντιπροσωπεύει την απουσία ορατής αλλαγής σε οποιαδήποτε μεταβολή, όπως σε σχήματα, φράσεις, φυσικούς νόμους, ή μαθηματικές εκφράσεις που μένουν απαράλλαχτα σε συγκεκριμένους μετασχηματισμούς. Σκεφτείτε, λόγου χάρη, τη φράση “Νίψον ανομήματα, μη μόναν όψιν”, η οποία είναι συμμετρική όταν διαβάζεται από το τέλος προς την αρχή γράμμα γράμμα. Δηλαδή παραμένει ίδια αν διαβαστεί ανάποδα. Ο τίτλος του ντοκιμαντέρ A Man, a Plan, a Canal, Panamaέχει την ίδια ιδιότητα. Οι φράσεις με τέτοιου είδους συμμετρία ονομάζονται καρκινικές, και αυτή η συμμετρία παίζει σημαντικό ρόλο στη δομή του φυλετικού χρωμοσώματος Υ. Μέχρι το 2003, οι βιολόγοι που μελετούν το γονιδίωμα πίστευαν ότι λόγω του γεγονότος ότι το χρωμόσωμα Υ δεν έχει συνοδό (με τον οποίο θα μπορούσε να ανταλλάξει γονίδια), το γενετικό του φορτίο θα υποβαθμιζόταν από ζημιογόνες μεταλλάξεις. Με έκπληξη όμως, οι ερευνητές που βρήκαν την ακολουθία του χρωμοσώματος Υ διαπίστωσαν ότι το χρωμόσωμα καταπολεμά την υποβάθμιση με τη βοήθεια της καρκινικής συμμετρίας: Περίπου 6 εκατομμύρια (από τα 50 εκατομμύρια) των γραμμάτων DNA του χρωμοσώματος σχηματίζουν καρκινικές αλληλουχίες. Αυτά τα κατοπτρικά αντίγραφα χρησιμεύουν ως αντίγραφα ασφαλείας για την περίπτωση ζημιογόνων μεταλλάξεων, και επιτρέπουν στο χρωμόσωμα, κατά κάποιο τρόπο, να ζευγαρώσει με τον εαυτό του – οι κλώνοι μπορούν να αλλάξουν θέσεις.

Οι διδιάστατες εικόνες και σχήματα, όπως αυτά που ζωγραφίζονται σε ένα φύλλο χαρτί, έχουν τεσσάρων ειδών συμμετρίες (όταν δεν επιτρέπονται εκτάσεις και παραμορφώσεις): ανάκλασης, περιστροφής, μετατόπισης, και ανάκλασης με ολίσθηση.

Συναντούμε τη συμμετρία ανάκλασης παντού τριγύρω μας – αυτή είναι η συνήθης αμφίπλευρη συμμετρία που χαρακτηρίζει τα ζώα. Τραβήξτε μια κατακόρυφη γραμμή στη μέση της εικόνας μιας πεταλούδας (βλ. εικόνα δεξιά). Μετά διπλώστε τη κατά μήκος αυτής της γραμμής. Η τέλεια σύμπτωση υποδεικνύει ότι η εικόνα της πεταλούδας μένει απαράλλαχτη αν ανακλαστεί κατά μήκος του διαμήκους άξονά της.

Πολλά γράμματα του αλφαβήτου έχουν επίσης αυτήν την ιδιότητα. Αν κρατήσετε μπροστά στον καθρέφτη ένα χαρτί με τη φράση “ΤΟ ΘΟΛΟ ΠΟΤΑΜΙ” γραμμένη κατακόρυφα, μπορεί να διαβαστεί κανονικά.

Η περιστροφική συμμετρία είναι επίσης πολύ διαδεδομένη στη φύση. Μια νιφάδα χιονιού (εικόνα δεξιά) περιστραμμένη κατά 60, 120, 180, 240, 300, ή 360 μοίρες γύρω από έναν άξονα που περνά από το κέντρο της (κάθετα στο επίπεδο) καταλήγει σε μια πανομοιότυπη διάταξη. Ένας κύκλος που περιστρέφεται κατά οποιαδήποτε γωνία γύρω από έναν άξονα που περνάει από το κέντρο του, κάθετα στο επίπεδο του κύκλου, παραμένει το ίδιο απαράλλαχτος.

Η συμμετρία μετατόπισης είναι η “ανοσία” σε αλλαγές που παρατηρείται σε επαναλαμβανόμενα σχέδια, όπως αυτό στη δεύτερη εικόνα. Μετατόπιση είναι μια μετακίνηση ή αλλαγή θέσης, κατά μια συγκεκριμένη απόσταση, κατά μήκος μιας γραμμής. Πολλές κορνίζες, ταπετσαρίες, παράθυρα ουρανοξυστών, ακόμα και οι σαρανταποδαρούσες, εμφανίζουν αυτό το είδος συμμετρίας.

Τέλος, οι αριστερές και οι δεξιές πατημασιές έχουν συμμετρία ανάκλασης με ολίσθηση (βλ. παρακάτω). Ο μετασχηματισμός σε αυτήν την περίπτωση αποτελείται από μια μετατόπιση (ολίσθηση) και μια ανάκλαση ως προς μια γραμμή παράλληλη προς την κατεύθυνση της μετατόπισης (διακεκομμένη γραμμή).

Όλες οι συμμετρίες που προαναφέρθηκαν είναι συμμετρίες σχήματος και μορφής – τέτοιες που μπορούν να παρατηρηθούν με τα μάτια μας. Οι συμμετρίες που αποτελούν τη βάση των θεμελιωδών νόμων της φύσης σχετίζονται με αυτές κατά κάποιο τρόπο, αλλά αντί να επικεντρώνονται στη μορφή, απαντούν μια διαφορετική ερώτηση: ποιοι μετασχηματισμοί μπορούν να πραγματοποιηθούν στον κόσμο γύρω μας που να αφήνουν απαράλλαχτους τους νόμους που διέπουν όλα τα παρατηρούμενα φαινόμενα;

Το μέτρο της συμμετρίας

Όλοι μαζί οι “νόμοι της φύσης” συνιστούν ένα σώμα κανόνων που θεωρείται ότι ερμηνεύουν κυριολεκτικά όλα όσα παρατηρούμε στο σύμπαν. Το γεγονός και μόνο ότι υπάρχει ένα τέτοιο σύνολο κανόνων, ήταν αδιανόητο πριν τον 17ο αιώνα. Μόνο με τις εργασίες επιστημονικών γιγάντων όπως του Γαλιλαίου (1564-1642), του Καρτέσιου (1596-1650), και, ειδικά, του Ισαάκ Νεύτωνα (1642-1727), έγινε σαφές ότι μια χούφτα νόμοι μπορούν να εξηγήσουν μια πληθώρα φαινομένων. Ξαφνικά, πράγματα φαινομενικά άσχετα μεταξύ τους, όπως η πτώση των μήλων, οι παλίρροιες, και η κίνηση των πλανητών, μπήκαν κάτω από την ομπρέλα του νόμου της βαρύτητας του Νεύτωνα.

Παρομοίως, με βάση τα εντυπωσιακά πειραματικά αποτελέσματα του Μάικλ Φαραντέι (1791-1867), ο Σκωτσέζος φυσικός Τζέιμς Κλαρκ Μάξγουελ (1831-1879) μπόρεσε να εξηγήσει όλα τα φαινόμενα του κλασικού ηλεκτρισμού, μαγνητισμού, και οπτικής με μόνο τέσσερις εξισώσεις! Αναλογιστείτε το για μια στιγμή – όλος ο κόσμος του ηλεκτρομαγνητισμού σε τέσσερις εξισώσεις.

Βρέθηκε ότι οι νόμοι της φύσης υπακούν σε μερικές από τις συμμετρίες που έχουμε ήδη συναντήσει, καθώς και μερικές άλλες, πιο ακατανόητες. Καταρχήν, οι νόμοι έχουν συμμετρία μετατόπισης. Η εκδήλωση αυτής της ιδιότητας είναι απλή: είτε πραγματοποιείτε ένα πείραμα στη Νέα Υόρκη, είτε στο Λος Άντζελες, είτε στην άλλη άκρη του Γαλαξία, είτε σε ένα γαλαξία δισεκατομμύρια έτη φωτός μακριά, μπορείτε να περιγράψετε τα αποτελέσματα χρησιμοποιώντας τους ίδιους νόμους. Πώς ξέρουμε ότι αυτό είναι αλήθεια; Επειδή οι παρατηρήσεις γαλαξιών σε όλο το σύμπαν δεν δείχνουν μόνο ότι ο νόμος της βαρύτητας είναι ο ίδιος παντού, αλλά και ότι τα άτομα υδρογόνου στο τέλος του παρατηρούμενου σύμπαντος υπακούν ακριβώς τους ίδιους νόμους του ηλεκτρομαγνητισμού και της κβαντομηχανικής που υπακούν και εδώ στη Γη.

Οι νόμοι της φύσης έχουν επίσης συμμετρία περιστροφής – οι νόμοι είναι ίδιοι είτε μετράμε αποστάσεις ως προς το βόρειο πόλο, είτε ως προς το γειτονικό καφενείο – η Φυσική δεν έχει προτιμητέα κατεύθυνση στο χώρο.

Αν δεν υπήρχε αυτή η αξιοπρόσεκτη συμμετρία των νόμων σε μετατοπίσεις και περιστροφές, δε θα υπήρχε καμιά ελπίδα να καταλάβουμε ποτέ τα διάφορα μέρη του σύμπαντος. Επιπλέον, ακόμα και εδώ στη Γη, αν οι νόμοι δεν ήταν συμμετρικοί, τα πειράματα θα έπρεπε να επαναλαμβάνονται συνεχώς σε κάθε εργαστήριο του κόσμου.

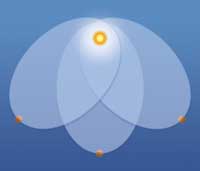
Θα πρέπει να προσέξουμε τη διαφορά μεταξύ των συμμετριών των σχημάτων και των συμμετριών των νόμων. Οι αρχαίοι Έλληνες πίστευαν ότι οι τροχιές των πλανητών γύρω από τον Ήλιο είχαν συμμετρία περιστροφής, ότι ήταν κυκλικές. Στην πραγματικότητα δεν έχουν συμμετρία περιστροφής οι τροχιές, αλλά ο νόμος της βαρύτητας του Νεύτωνα. Αυτό σημαίνει ότι οι τροχιές μπορεί να είναι (και πράγματι είναι!) ελλειπτικές, και να έχουν οποιονδήποτε προσανατολισμό στο χώρο (βλ. εικόνα αριστερά).

Στην εισαγωγική παράγραφο, δεν είπαμε απλώς ότι οι νόμοι ακολουθούν ορισμένες συμμετρίες, αλλά ότι η συμμετρία μπορεί να είναι η πηγή των νόμων. Τι σημαίνει αυτό;

Η πηγή των φυσικών νόμων

Φανταστείτε ότι δεν έχετε ξανακούσει για νιφάδες, και κάποιος σας ζητά να μαντέψετε το σχήμα τους. Προφανώς πρόκειται για κάτι ακατόρθωτο. Απ’ αυτά που ξέρετε, μια νιφάδα θα μπορούσε κάλλιστα να μοιάζει με τσαγιέρα, με το γράμμα Σ, ή με τον Μπαγκς Μπάνι.

Ακόμα και αν σας έδιναν το σχήμα μιας ακτίνας της νιφάδας (εικόνα δεξιά, a) και σας έλεγαν ότι αυτό είναι μέρος το συνολικού της σχήματος, δε θα βοηθούσε πολύ. Η νιφάδα θα μπορούσε να μοιάζει, για παράδειγμα, με τη διάταξη b. Από την άλλη πλευρά, αν σας έλεγαν ότι η νιφάδα έχει συμμετρία περιστροφής 60 μοιρών, αυτή η πληροφορία θα μπορούσε να αξιοποιηθεί πολύ αποτελεσματικά. Η συμμετρία περιορίζει αμέσως τις πιθανές διατάξεις, σε εξάγωνες, δωδεκάγωνες, δεκαοχτάγωνες, κ.ο.κ., νιφάδες. Θεωρώντας, με βάση την εμπειρία, ότι η φύση προτιμά την απλούστερη, πιο οικονομική λύση, η εξάγωνη νιφάδα (c) θα ήταν μια πολύ λογική εικασία. Με άλλα λόγια, η απαίτηση για ύπαρξη συμμετρίας στο σχήμα, μας οδήγησε στη σωστή κατεύθυνση.

Κατά τον ίδιο τρόπο, η απαίτηση οι νόμοι της φύσης να είναι συμμετρικοί σε συγκεκριμένους μετασχηματισμούς, δεν υπαγορεύει μόνο τη μορφή αυτών των νόμων, αλλά επιπλέον, σε μερικές περιπτώσεις, επιβάλλει την ύπαρξη δυνάμεων ή άγνωστων ακόμα στοιχειωδών σωματιδίων. Επιτρέψτε μου να το εξηγήσω χρησιμοποιώντας δύο ενδιαφέροντα παραδείγματα.

Ένας από τους στόχους του Αϊνστάιν όταν εξηγούσε τη γενική σχετικότητα ήταν να φτιάξει μια θεωρία στην οποία οι νόμοι της φύσης θα έμοιαζαν ίδιοι για όλους τους παρατηρητές. Δηλαδή οι νόμοι έπρεπε να είναι συμμετρικοί με οποιαδήποτε μεταβολή του σημείου παρατήρησης στο χώρο και στο χρόνο (στη Φυσική αυτό ονομάζεται “αναλλοίωτο”). Ένας παρατηρητής που στέκεται πάνω σε μια γιγαντιαία χελώνα θα πρέπει να βρει τους ίδιους νόμους με έναν παρατηρητή που βρίσκεται σε ένα καρουζέλ ή σε έναν πύραυλο που επιταχύνεται. Πράγματι, αν οι νόμοι είναι παγκόσμιοι, γιατί θα πρέπει να εξαρτώνται από το αν ο παρατηρητής επιταχύνεται;

Αν και η απαίτηση του Αϊνστάιν για συμμετρία ήταν απολύτως λογική, δεν ήταν καθόλου τετριμμένη. Έπειτα, ένα εκατομμύριο αυχενικοί τραυματισμοί το χρόνο στις Ηνωμένες Πολιτείες, δείχνουν ότι αισθανόμαστε την επιτάχυνση. Κάθε φορά που ένα αεροπλάνο πέφτει σε αναταράξεις, αισθανόμαστε το στομάχι μας να πηγαίνει πάνω-κάτω. Φαίνεται επομένως ότι υπάρχει μια αλάθητη διάκριση μεταξύ ομαλής και επιταχυνόμενης κίνησης. Τότε πώς μπορεί οι νόμοι της φύσης να είναι οι ίδιοι για τους επιταχυνόμενους παρατηρητές, όταν αυτοί οι παρατηρητές φαίνεται να δέχονται επιπλέον δυνάμεις;

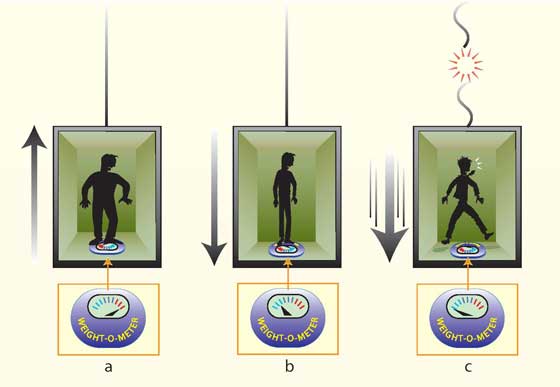
Σκεφτείτε την εξής κατάσταση. Αν στέκεστε σε μια ζυγαριά μέσα σε έναν ανελκυστήρα που επιταχύνει προς τα πάνω, τα πόδια σας εξασκούν μεγαλύτερη πίεση στη ζυγαριά – οι ζυγαριά θα δείξει μεγαλύτερο βάρος (βλ. εικόνα κάτω, a). Το ίδιο θα συμβεί, όμως, και σε έναν ακίνητο ανελκυστήρα αν η βαρύτητα για κάποιο λόγο γίνει ισχυρότερη. Ένας ανελκυστήρας που επιταχύνει προς τα κάτω θα μοιάζει με παρουσία ασθενέστερης βαρύτητας (b). Αν το καλώδιο του ανελκυστήρα σπάσει, εσείς και η ζυγαριά θα εκτελείτε μαζί ελεύθερη πτώση, και η ζυγαριά θα δείξει μηδενικό βάρος (c). Η ελεύθερη πτώση είναι επομένως ισοδύναμη με το να απαλείψουμε, ως εκ θαύματος, τη βαρύτητα. Αυτό οδήγησε τον Αϊνστάιν το 1907 σε ένα συγκλονιστικό συμπέρασμα: η δύναμη της βαρύτητας και η δύναμη που προκύπτει λόγω επιτάχυνσης είναι στην πραγματικότητα μία και αυτή. Αυτή η δραστική ενοποίηση ονομάστηκε “αρχή της ισοδυναμίας”, υποδηλώνοντας ότι η επιτάχυνση και η βαρύτητα είναι στην πραγματικότητα δύο όψεις της ίδιας δύναμης – είναι ισοδύναμες.

Σε μια διάλεξή του στο Κιότο το 1922, ο Αϊνστάιν περιέγραψε τη στιγμή της επιφοίτησης που είχε το 1907: “Καθόμουν στο γραφείο ευρεσιτεχνιών στη Βέρνη και ξαφνικά σκέφτηκα κάτι: Αν κάποιος πέφτει ελεύθερα δε θα αισθάνεται το βάρος του. Ξαφνιάστηκα. Αυτή η απλή σκέψη μου έκανε μεγάλη εντύπωση. Με ώθησε προς μια θεωρία της βαρύτητας”.

Η αρχή της ισοδυναμίας είναι πραγματικά η εκδήλωση μιας γενικής συμμετρίας: Οι νόμοι της φύσης – όπως εκφράστηκαν από τις εξισώσεις της γενικής σχετικότητας του Αϊνστάιν – είναι οι ίδιοι σε όλα τα συστήματα, συμπεριλαμβανομένων αυτών που επιταχύνονται. Γιατί όμως υπάρχουν προφανείς διαφορές ανάμεσα σε ό,τι παρατηρείται σε ένα καρουζέλ και σε ένα ακίνητο εργαστήριο; Η γενική σχετικότητα παρέχει μια εκπληκτική απάντηση. Οι διαφορές αυτές έχουν να κάνουν μόνο με το περιβάλλον, όχι με τους ίδιους τους νόμους. Παρομοίως, οι κατευθύνσεις πάνω και κάτω φαίνονται διαφορετικές στη Γη λόγω της γήινης βαρύτητας. Οι ίδιοι οι νόμοι της φύσης δεν έχουν προτιμητέα κατεύθυνση (έχουν περιστροφική συμμετρία)· δεν ξεχωρίζουν το πάνω και το κάτω. Οι παρατηρητές πάνω σε ένα καρουζέλ, σύμφωνα με τη γενική σχετικότητα, νιώθουν τη φυγόκεντρο δύναμη η οποία είναι ισοδύναμη με τη βαρύτητα. Το συμπέρασμα είναι πραγματικά εντυπωσιακό: Η συμμετρία των νόμων σε οποιαδήποτε μεταβολή των συντεταγμένων του χωροχρόνου επιβάλλει την ύπαρξη της βαρύτητας! Αυτό εξηγεί γιατί η συμμετρία είναι η πηγή των δυνάμεων. Η απαίτηση για συμμετρία δεν αφήνει περιθώρια επιλογής στη φύση: η βαρύτητα

Download

Download this article as a PDF