Ebola med tal: at bruge matematik for at tackle epidemier Understand article
Oversat af: Jørgen Wilhelmsen. At undersøge hvordan infektionssygdomme spredes kan se ud som om, det kun handler om medicin – men at undersøge antallet af tilfælde i detaljen kan også give os mange oplysninger.
Under den seneste Ebola epidemi i Vestafrika begyndte lufthavne i USA og Europa at screene rejsende fra høj risiko områderne for Ebola symptomer herunder en hævet legemstemperatur. Dette så ud som en rimelig forholdsregel – men en ny undersøgelse baseret på beregninger af kendte fakta om sygdommen viste at screeningen sandsynligvis aldrig kunne blive effektiv.

ankommer med fly vil
sandsynligvis ikke forhindre
spredningen af Ebola
Billede med tilladelse fra
KlausF; Billedkilde: Wikimedia
Commons
Undersøgelsen, publiseret i “British Medical Journal (Mabey et al. 2014)”fandt at: ”en adgangs screenings politik ikke vil have nogen rimelig effekt mht. risikoen for import af Ebola til UK”. Forfatternes argumentation er lige ud af landevejen: Antag at en rejsende allerede viser Ebola symptomer ved afrejsen og forhindres i at boarde et fly, i forhold til en anden passager, som ikke er syg ved afrejsen, men som så senere vil blive diagnosticeret ved ankomsten, da vil passageren have udviklet symptomerne på selve flyvningen. Fordi den gennemsnitlige inkubationstid for sygdommen er temmelig lang (omkring en uge), så vil sandsynligheden for at en person bliver opdaget som ebolapatient på denne måde være lav – ikke mere end 13% i bedste fald. Idet lufthavns screening er kostbar foreslår forfatterne at pengene ville være bedre brugt i Afrika for at forhindre en omfattende og skræmmende humanitær krise.
Basal matematik
Meget kan man finde ud af ved hjælp af basal matematik – men man skal altid være omhyggelig med at bestemme, hvilke tal man vil bruge. Tidligt under Ebola epidemien regnede man med at døds raten var omkring 50% – et tal der blev beregnet ved at dividere antallet af døde med antallet af rapporterede tilfælde. Men denne metode tog ikke hensyn til det faktum, at de personer, der var i live men smittede, ville dø af sygdommen. Dette førte til en undervurdering af den reelle døds rate.

bliver screenet for Ebola i
Chicago´s O´Hare airport
Billede med tilladelse fra
Melissa Maraj, US Customs and
Border Protection; billedkilde:
Wikimedia Commons
“Denne fejl skete ofte, og (50% tallet) blev ofte citeret,” udtaler Adam Kucharski fra UK’s London School of Hygiene and Tropical Medicine, en kollega til forfatterne af undersøgelsen om lufthavns screeningen. ”Ved en meget simpel analyse forsøgte jeg selv og min kollega at justere estimatet. Vi fandt ud af at døds raten sandsynligvis er omkring 70%, hvilket senere kliniske studier er enige i.”
Et meget vigtigt tal ved starten af en epidemi er det basale reproduktions tal, almindeligvis betegnet med R0. Dette tal måler det gennemsnitlige antal af mennesker, som en inficeret person vil smitte, under den forudsætning at ingen i befolkningen er immune overfor sygdommen. I Ebolas tilfælde blev R0 ved starten af sygdomsudbruddet estimeret til at være mellem 1,5 og 2, hvilket er et tal som ligner tallet for en influenza epidemi. Mæslinger, en luftbåren og meget smitsom sygdom, har en R0 på omkring 18.
Igen, vil noget basal matematik være en hjælp til at give en grov ide om, hvor hurtigt en infektionssygdom vil spredes. Hvis en sygdom har en R0 værdi på 2 og en tilfældig inficeret person smitter 2 andre i løbet af 2 uger efter personen selv fik sygdommen, som så sammen inficerer 4 andre i de næste to uger osv. Dette er en eksponentiel vækst, som stiger meget hurtigt: efter blot 20 uger vil sygdommen have inficeret:
1 + 2 + 4 + 8 + … + 210 = 2047 mennesker
Denne model over-simplificerer selvfølgelig. Selv om man ofte ser en eksponentiel vækst ved en epidemis start, så har epidemiologer mere sofistikerede modeller til at forudsige en epidemis spredning. (se Keeling, 2001, og Kucharski, 2011). Imidlertid kan vi nemt se betydningen af R0: Den same beregning for mæslinger vil have den samlede befolkning i verden inficeret indenfor 16 dage.
R0 er kun en gennemsnitlig værdi målt i hele populationen, så det næste må være at forstå, hvorledes denne værdi varierer. For eksempel foreslår (Yamin et al, 2015) at patienter med Ebola bliver mere smittefarlige i de senere stadier af infektionen, så at placere patienter i isolation i disse sene stadier – og selv efter døden, når kroppen bliver forberedt til at blive begravet – vil have en større effekt end at undersøge dem for infektionen tidligere i forløbet.
Tilfældighed og usikkerhed
Selvfølgelig er tilfældighed en vigtig faktor – specielt i begyndelsen af et udbrud. Den første patient i Sierre Leone, hvor mange tusinde døde, var tilfældigvis en traditionel medicinmand (healer). Hvis begravelse tiltrak en stor folkemængde. De mennesker der berørte healerens inficerede krop tog sygdommen med, når de rejste videre.
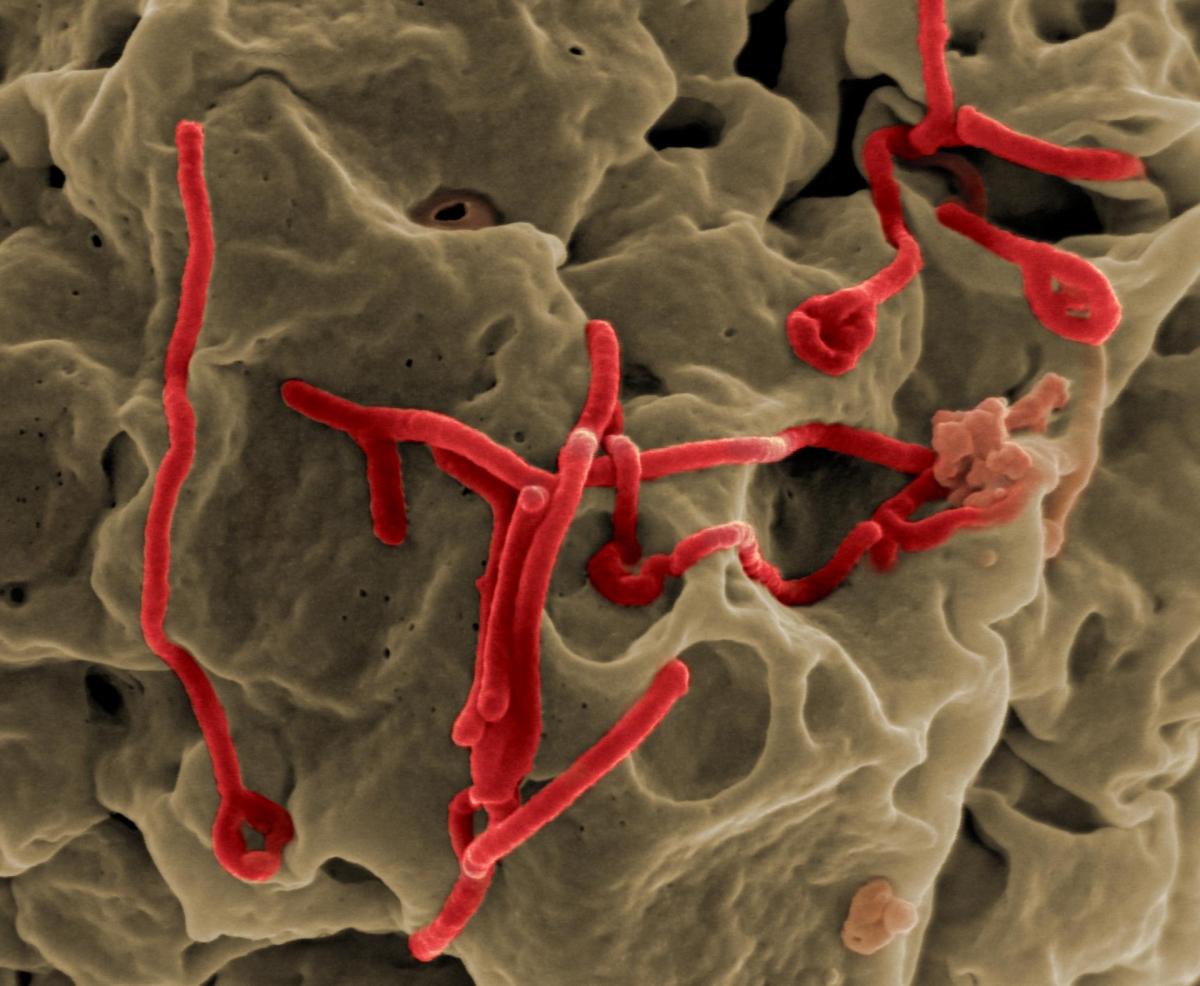
virus knopskydende fra en
celles overflade
Billede med tilladelse fra
National Institute of Allergy
and Infectious Diseases (NIH);
billedkilde: Flickr
“I de situationer hvor der er et meget lille antal syge kan en bestemt hændelse, der finder sted, betyde at vi får et meget anderledes udbrud,” udtaler Adam Kucharski. Atter er R0 , det basale reproduktionstal, en vigtig faktor i forhold til hvad der sandsynligvis sker. Sandsynligheden for at et sygdomsudbrud vil udvikle sig til en større epidemi kan beregnes til at være 1-1/R0 (i Kucharski 2011). Med en R0 på mellem 1,5 og 2 for Ebolas vedkommende, så vil risikoen blive et sted mellem 1/3 og ½ dvs. mellem 33 – 50%, Vi må siges at have være en smule uheldige.
Der er andre type typer af usikkerhed når det drejer sig om at forudsige forløbet af en sygdom eller betydningen af forholdsregler mod sygdommen. Der kan være en mangel ved modellen, eller en oprindelig usikkerhed med en vigtig parameter, som R0, der kan vokse, når modellen simulerer begivenheder længere ude i fremtiden. Kendt som sommerfugle effekten er dette grunden til hvorfor mange fænomener, som fx vejret eller aktie markedet er så vanskelige at forudsige.
Så hvordan kan vi håndtere sådanne usikkerheder? ”Jeg tror at modelbyggere sommetider skal være ydmyge og fastslå at de ikke kan forudsige så langt ude i fremtiden,” siger Adam K. ”Folk kan lide at få et bestemt tal; journalister specielt er ivrige efter at skrive om dem. Men som ved alle forudsigelser er det, at offentliggøre blot et enkelt tal en farlig sag.
Undertiden er resultatet af en undersøgelse dog ret overbevisende, på trods af en indbygget usikkerhed – undersøgelsen om effektiviteten af lufthavns screeningen fx ”Introduktionen af disse screeninger var i høj grad en politisk, og ikke en videnskabelig beslutning”, konkluderer Adam K. Vi kan alle blive styret af vores angst, men forudsigelserne af en nøje afprøvet, evidens-baseret matematisk model er sandsynligvis en bedre rettesnor for handling.
Mere om Ebola
- Ebola er en alvorlig og ofte dødelig sygdom hos mennesket.
- Virus overføres til mennesket fra vilde dyr, når den optræder i den menneskelige population spredes den fra person til person.
- Det første kendte udbrud af Ebola optrådte i fjerne landsbyer i Central Afrika tæt ved tropiske regnskove. Det nyeste udbrud i Vestafika har imidlertid været i store byområder så vel som på landet.
- Overlevelse kan fremmes ved en tidlig behandling med væsketilførsel og symptombehandling. Indtil videre er der ingen bestemt behandling af Ebola, men en mængde blod -, immunologiske – og medicinske behandlinger er under udvikling.
- I øjeblikket findes ingen official Ebola vaccine men to potentielle muligheder bliver evalueret.
Kilde: The World Health Organization, April 2015
Acknowledgement
Denne artikel blev oprindelig publiseret i en længere form i Plus magazinew1, et gratis online magasin som åbner dørene til en matematisk verden med al dens skønhed og til matematiske anvendelser.
References
- Keeling M (2001) The mathematics of diseases. Plus Magazine.
- Kucharski A (2011) Keeping track of immunity. Plus Magazine.
- Mabey D, Flasche S, Edmunds WJ (2014) Airport screening for Ebola. British Medical Journal 349: g6202. doi: 10.1136/bmj.g6202
- Yamin D et al (2015) Effect of Ebola progression on transmission and control in Liberia. Annals of Internal Medicine 162(1): 11–17. doi: 10.7326/M14-2255. Denne artikel kan frit downloades fra journalens hjemmeside. www.annals.org
Web References
- w1 – Den originale artikel publiseret i Plus Magazine er frit tilgængelig online.
Resources
- For flere informationer om Ebola:
- The World Health Organization’s factsheet
- Kucharski AJ, Piot P (2014) Containing Ebola virus infection in West Africa. Eurosurveillance 19(36): pii=20899. Denne artikel kan frit downloades fra journalens hjemmeside: www.eurosurveillance.org
-
Du kan nu now join deltage i kampen mod Ebola ved at downloade en gratis App og give din ledige computerkraft til the Outsmart Ebola Together computer projekt. Ideen er at forme en virtuel supercomputer, som dannes udfra de donerede computer hukommelser fra (forhåbningsfulde) ti tusinder af frivillige som vil screene millioner af molekyler som kunne tænkes at uskadeliggøre virusen. De bedste kan blive testet i laboratorier måske blive modificeret til at virke bedre og de kan måske blive til en anti-viral medicin.
-
Besøg Plus Magazine website for at finde klasserums aktiviteter classroom activity omkring epidemiologiske modeller. Der bruges basal sandsynlighedsregning og arbejdet kan bruges til at diskutere eksponentiel vækst og geometrisk udvikling.
- For at lære mere om spredningen af infektionssygdomme se:
- Bos K (2014) Tales from a plague pit. Science in School 28: 7–11.
- Heymann J (2013) Evolving threats: investigating new zoonotic infections. Science in School 27: 12-16.
- Niekoop L, Rienks F (2006) The ecologist’s view of bird flu. Science in School 3: 24–30.
- Quammen D (2012) Where will the next pandemic come from? and how can we stop it? Popular Science.
Review
At undervise i sandsynlighed og statistik er ikke let; en af de væsentlige grunde hertil er vanskeligheden ved at finde interessante eksempler som er relevante for elevernes liv. Denne artikel er derfor et nyttigt hjælpemiddel; Ebola har været i nyhederne i månedsvis, og mange mennesker, selv yngre elever, er bekymrede for risikoen for at få sygdommen.
Artiklens vigtigste formål er at skabe en stærk forbindelse mellem matematik og biologi. Den giver et eksempel på hvor vigtigt det er med korrekte data for medicin og sundhedsvæsenet, herunder hvorledes data bliver indsamlet, bearbejdet og præsenteret. Fortolknings fejl dækkes ligeledes i artiklen, hvilket kunne føre til en diskussion af hvorledes statistik kan bruges og misbruges.
Mange fællesfaglige aktiviteter kunne baseres på artiklen. Som for eksempel baseret på biologi, sandsynlighedsregning og statistik, historie, økonomi og geografi. Artiklen kunne også bruges som en basis for at dække emner som populationsdynamik og effekter af moderne rejseaktivitet; smitte spredning; offentlige budgetter mht. sundhed og velfærd; forbindelse mellem sygdom og økonomi; data journalistik, en metode til at dække nyheder om hændelser og fakta ud fra en stor numerisk analyse; og hvordan man læser og diskuterer en artikel, som er baseret på statistik. Endelig kan artiklen bruges til at introducerer modellering, et fundamentalt begreb i naturvidenskab, og hvorledes dette er baseret på data, eller modsat hvorledes data passes ind i en given model.
Forståelse og perspektiverings spørgsmål kunne være:
-
Hvad menes der med “high-risk lande”? Lav en liste over nogle high-risk lande mht. Ebola.
-
Hvor lang er den gennemsnitlige tid det tager mellem udsættelsen for Ebola virus og at få symptomer?
-
Hvad er “reproduktionstallet” og hvorfor er det vigtigt?
-
Hvad er “eksponentiel vækst”?
Marco Nicolini, Liceo Scientifico Statale Alessandro Tassoni, Modena, Italien





