Geometry can take you to the Moon Teach article
Measure the distance from Earth to the Moon using high-school geometry and an international network of schools and observatories.

Image courtesy of NASA
Imagine stretching your arm out and looking at your thumb, first with one eye, then with the other. The apparent shift of your thumb with respect to the background is called parallax. The same principle applies if two different schools ‘look’ at the Moon: they will see it slightly shifted with respect to the stars in the background.
In this activity, schools in different continents pair up so students aged 16-19 can compare their observation of the Moon across distances and calculate Earth’s distance to it (figure 1). Equipped with only a good camera and a good knowledge of geometry, the observation takes approximately 2 hours and the calculation 3 hours (establishing the partnership might take a little longer…).
Defining the right conditions
The overall observation plan for the activity is detailed in figure 1, where M is the Moon, depicted as a point because its size is very small compared to the distance calculated (approximately 1/100th).
As in many scientific endeavours, planning is key. In this case, in addition to defining the right conditions to make the observations, the teacher needs to determine what margin of error is acceptable: this is important so the pupils are not disappointed if they don’t find the exact distance. Below we list a number of important points to highlight when discussing the activity with the class, but also when setting up the partnership with another school.
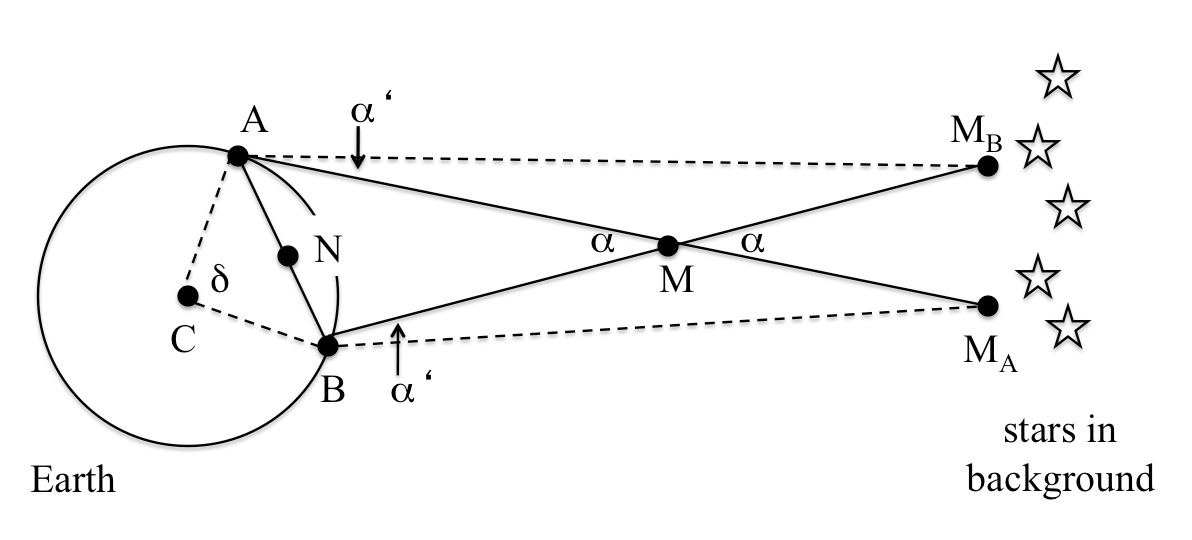
Image courtesy of the authors
Figure 1 shows how two observers (A and B) will see the Moon, M, as being in two slightly different positions in the sky. While in practice the two observation points, A and B, M, and the centre of Earth, C, do not lie on the same plane, to simplify the calculations so that we can use plane trigonometry alone we assume that they do.
celestial body.
Image courtesy of Nicola Graf
For that approximation to be as exact as possible, the two observation points need to be at the same longitude, and the Moon should be at its highest point (in culmination)w1 at the moment of the observation. This ideal situation is very difficult to obtain but we recommend that you stay as close to it as possible, and that you are aware of the errors implied by sizeable deviations from such conditions.
Moreover, if the Moon’s angle with the celestial equator (declination)w1 is equal to the average of the latitudes of A and B, ABM forms an isosceles triangle and this further simplifies the calculations.
Having the right sky in the background
You will also need at least two bright starsw1 (or planets) in the background to find the two apparent positions of the Moon, MA and MB.
Geometrical assumptions
Then we will consider that the two straight lines AMA and BMA are almost parallel, as are AMB and BMB. This would mean that the angles α ≈ α’ (figure 1). While not strictly true, this assumption is acceptable, as the pairs of lines converge far from both Earth and the Moon. Of course, this appears to be very far from true in figure 1, because it is not drawn to scale.
If we measure the angle α and the distance AB – known as the baseline – plus another angle in the triangle ABM, we can calculate all the other distances. Otherwise, we can make the triangle ABM become isosceles, and knowledge of a and AB is sufficient to calculate all the distances.
A key point is that the baseline must be long enough, when compared to the distance we want to find, to prevent the parallax from becoming vanishingly small. For the Moon, a distance between the partner schools of around 1000 km is enough, but the larger it is, the better.
But there will still be errors…
Despite all the care that will go into choosing the best conditions, the measurements will not be perfect. The main sources of error are:
- Imprecision in spotting the shift of the Moon in the two images, mainly because of overexposure of the Moon’s disk;
- A, B, C and M not lying exactly in a plane;
- Distortions due to camera lenses;
- Observation conditions;
- Atmospheric refraction;
- Time synchronisation.
Errors due to d) and e) are not very important: our measurement is based upon large angles and so is not affected greatly by an imprecision of a few arcseconds.
Time synchronisation (f) is not very important either because the Moon travels the equivalent of its own diameter in one hour, so an imperfect synchronisation of a few seconds (or even minutes) is not relevant.
Distortions due to camera lenses (c) can be reduced if a small angle of view is used, like the one provided by a telephoto lens. A normal camera lens introduces a larger, but still acceptable, error. In our case, that angle was not so small and we estimate it generated an imprecision of approximately 1-2%.
Errors due to a) and b) are the most important and can account for an imprecision of 5-10% each. Together, they account for an overall error of about 10-20%. To reduce a) we must choose a long parallax baseline so that the shift of the Moon is as large as possible; to reduce b) we must properly choose places and moments for observations so that A, B, C and M lie in the same plane. If both conditions hold (for us, the first condition did but the second didn’t), the error can be reduced to a few percent.
The parallax network
We set up a network of schools, observatories and educators across the planet to undertake this measurement. It is made up of the following members:
- Mario Koch, teacher at the Friedrich-Schiller-Gymnasium in Weimar, Germany
- Noorali Jiwaji, physics lecturer at the Open University of Tanzania in Dar es Salaam, Tanzania
- Frank Oßwald, teacher at the Goethegymnasium in Weissenfels, Germany
- Matthias Penselin, teacher at Albert Schweitzer Gymnasium Crailsheim and at the House of Astronomy in Heidelberg, Germany
- Alexander GM Pietrow, Iosto Fodde and Jelle Mes, students from Leiden Observatory and members of the observing committee of the Leidsch Astronomisch Dispuut ‘F. Kaiser’, Leiden, Netherlands
- Elena Servida, teacher at Liceo Vittorio Veneto in Milan, Italy
- Brian Sheen, Roseland Observatory, St Austell, UK
With this network, or their own, teachers can propose dates to carry out lunar observations to work out the distance from Earth to the Moon.
The long distances between the schools in our network provide a sufficiently long baseline (distance AB) to make it possible to measure Earth’s distance from Mars in May 2016 (Cenadelli et al, 2009; Penselin et al, 2014). At that time, Earth will be situated between the Sun and Mars, and Mars will be almost at its closest possible distance to Earth, an ideal position for such observations.
If you would like to contact any part of this international network to perform measurements, please contact Davide Cenadelli at davide.cenadelli@unimi.it
Material
The only specific material necessary is a good camera to take photos of the Moon and the sky. A telephoto lens with a focal length of around 100–200 mm is the best choice, but a normal lens will also work if the bright stars or planets in the background are not very close to the Moon.
Procedure
- Use the parallax network (see box) to find a school or observatory that is on a similar longitude to your school.
- Note the latitude and longitude of the two partners (λ = latitude, l = longitude). Here, we use observations taken in Cape Town, South Africa, and at the Astronomical Observatory of the Autonomous Region of the Aosta Valley (OAVdA), Italy:
OAVdA, Italy: (λI 45.78° N, lI 7.48° E)
Cape Town, South Africa: (λS 33.93° S, lS 18.42° E) - Agree the exact dates and times for the Moon observations (it is better to plan for several dates, in case the weather is bad). The two observers above agreed to make a simultaneous observation on 2 February 2015 at 20.02 UT. That evening there were two bright reference bodies, Jupiter and Procyon (α CMi), in the sky not far from the Moon, which could serve as reference points against which to measure the position of the Moon.
The best circumstances are when bright background planets or stars, such as Jupiter and Procyon, are visible in the Moon’s proximity, and ideally as close as possible to it so that a telephoto lens with a small field of view can be used. This helps to avoid the large perspective distortion effects typical of wide-field lenses. - On the chosen date, all participants with clear skies should take several images of the Moon with a camera, following the predefined time schedule. The images need to show as clearly as possible the Moon and the two bright reference bodies. They should be captured with different exposure times, in order to choose the best compromise between a not overwhemingly bright Moon and yet visible background stars.
- Superimpose the images from two different observers into a single image, as in figure 2.

Image courtesy of the authors
- Measure the distance from Jupiter to Procyon on one image, and rescale the other image to match that distance so that both images are on the same scale;
- Superimpose the images and mark the position of the Moon as seen from both schools on the same image;
- Measure the shift of the centre of the Moon.
- Calculate the parallax baseline, AB, as shown in figure 1.
The angle, δ, between the two observers A and B can be calculated as follows (Roy & Clarcke (1977):
cos δ = sin λI sin λS + cos λI cos λS cos(lI − lS )
= −sin (45.78°) sin (33.93°) + cos (45.78°) cos (33.93°) cos (10.94°)
= 0.1681
Thus δ = 80.32° (1)
If we assume that Earth is perfectly spherical and its radius is 6367 km, the baseline AB is given by:
AB = 2BN
= 2(CB * sin (δ/2))
= 2 × 6367 km × sin (80.32°/2)
= 8212 km (2) - Calculate the parallax angle, α.
By simply using a ruler, we can estimate that the shift of the Moon that we observed (figure 2) is about 2.4 lunar diameters. As seen from Earth, the lunar diameter subtends an angle of 0.5°; that is, if we draw two lines from the eye of an observer to the extremes of the lunar diameter, the angle between the lines is 0.5°.
Therefore if one lunar diameter corresponds to 0.5° and the apparent shift of the Moon we observed is 2.4 lunar diameters, then:
α = 2.4 * 0.5 = 1.2° - Calculate the distance between the Moon and the centre of the Earth, CM.
We will calculate CM in two cases. In both cases we assume that A, B, M and C lie in the same plane.
Case 1: ABM is an isosceles triangle
In this case, the angles BAM and ABM are equal, and:
CM = CN+NM
= CA cos δ/2 + ([AB/2]/[tan α/2])
= 4866 + 392 080 km
= 396 900 km (3)
The known distance at the time of measurementw1 was 397 900 km, so we obtained a value that is underestimated by a mere 0.3%. Because of the approximations we used, this accuracy was partly a matter of luck.
Case 2: ABM is not an isosceles triangle
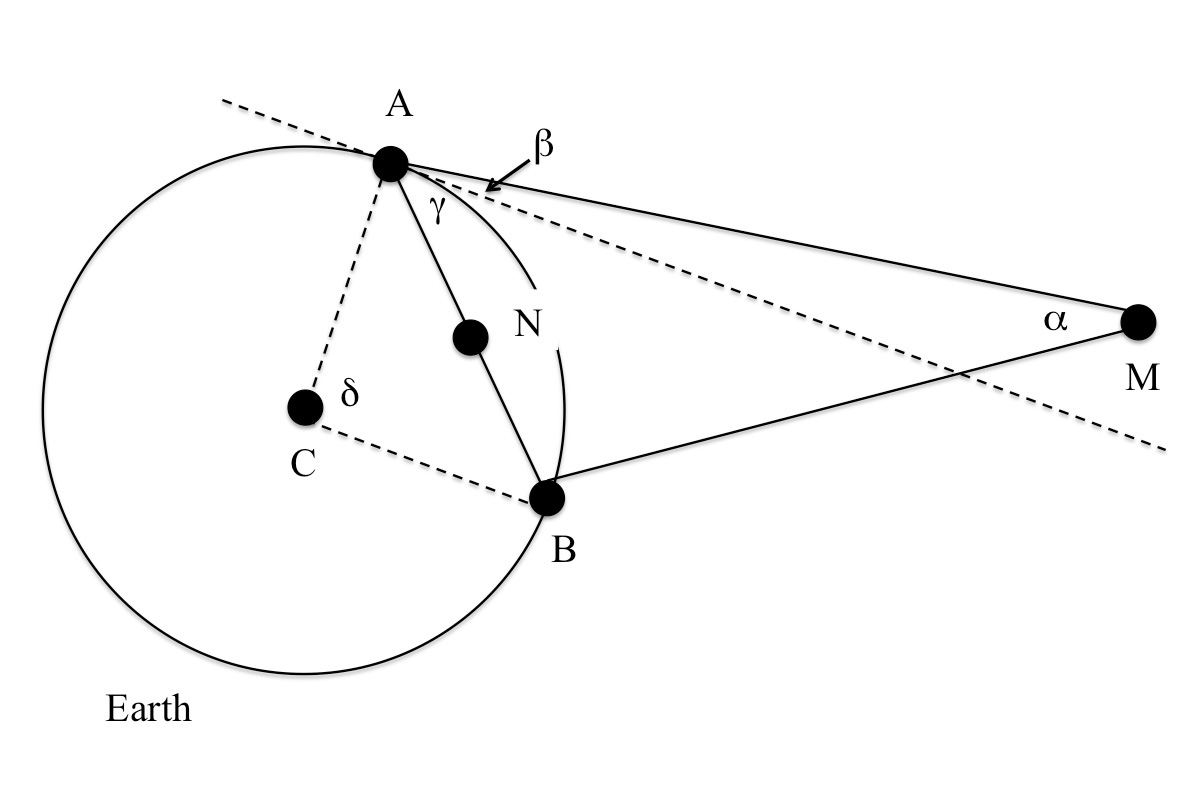
Figure 3: Close-up of the section of figure 1 showing the space between Earth and the Moon, and the angles β and γ.
Image courtesy of the authorsIf we drop the assumption that AMB is an isosceles triangle, we need to know the value of another angle, such as BAM. BAM is equal to the sum of β, i.e. the altitude of the Moon above the horizon from A, and γ (see figure 3). β can be measured with proper equipment or, in its absence, can be taken to be almost equal to the altitudew1 of one of the reference stars or planets we used to measure the shift of the Moon. For Procyon, we had β = 39.3°.
We can calculate γ using the value for δ that we calculated earlier and the geometry rule that says: γ = δ/2.
It follows that BAM = β + γ = 79.5°.
Finally, if we apply the law of sines to triangle ANM, we have:
ΝM/sin79.5° = AN/sin(α/2)
ΝM = AN (sin79.5°/sin0.6°)
≈ 385 536 km (4)
and hence:
CM = CN + NM
= CAcosα/2 + NM
= 4866 + 385 536 km = 390 400 km (5)
This result is still realistic and only 1.9% less than the known value.
Acknowledgments
The authors wish to warmly thank all participants in our network, as well as the students who participated in the ESO Camp 2014 who performed a similar measurement.
The Astronomical Observatory of the Autonomous Region of the Aosta Valley is supported by the Regional Government of the Aosta Valley, the Town Municipality of Nus and the Mont Emilius Community. Andrea Bernagozzi has carried out part of the work for this project while supported by a grant from the European Union-European Social Fund, the Autonomous Region of the Aosta Valley and the Italian Ministry of Labour and Social Policy.
References
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11: 72-77
- Roy AE, Clarcke D (1977) Astronomy: Principles and Practice. Bristol, UK: Adam Hilger. ISBN: 0852743467
Web References
- w1 – To find the values needed to perform the calculations described in the article, you can use the sky simulator Stellarium, a free open-source planetarium for your computer.
Resources
- The method used in this article is also described in many astronomy textbooks. For example, see:
- Karttunen H et al (2007) Fundamental Astronomy 5th edition. Berlin, Germany: Springer. ISBN: 9783540341437
- Didactic material related to Penselin et al (2014), which is directly usable in the classroom, can be found on the website of Wissenschaft in die Schule (in German only).
Review
This article describes a nice way to bring together mathematics with other science subjects, such as physics. It shows how to calculate the distance to the Moon or even Mars by using your own data from camera images and from your partner institution (e.g. the parallax network). Using pure mathematics – or pure applied mathematics, since you are solving a real problem – you will get good results.
Because of its short but efficient introduction, this article can be used either by science or by mathematics teachers.
Gerd Vogt, Higher Secondary School for Environment and Economics, Yspertal, Austria





