Exploring anamorphosis: revealing hidden images with mirrors Teach article

Author(s): Yajie Liang

Through the looking glass: unlock the secrets of anamorphosis, where art and science meet to create mind-bending illusions!

Metal cylinder reflecting the distorted image of a butterfly on a blue background.
Image courtesy of Martina Marzullo, butterfly image adapted from Rawpixel, Public Domain

Anamorphosis – a term derived from the Greek words ‘ana’, meaning ‘back’, and ‘morphe’, meaning ‘form’ – essentially refers to a visual technique that distorts an image in a way that it can only be fully perceived when viewed from a specific vantage point or with the aid of a particular device. This phenomenon has intrigued artists and scientists alike for centuries, and offers a fascinating journey into the world of distorted images and optical illusions, with famous examples like Hans Holbein’s The Ambassadors, where a skull is only visible if you look at the painting at an angle, and Leonardo da Vinci’s anamorphic eye drawings.[1]

An example of anamorphosis in the Holbein painting The Ambassadors
© The National Gallery, London

One of the most intriguing methods of creating anamorphic images is to use mirrors. When an image is painted onto a flat surface and viewed on a cylindrical mirror placed next to it, for example, the distorted elements ‘magically’ transform into a coherent, recognizable image. Last year, the Mathematik-Informatik-Station (MAINS) in Heidelberg hosted the exhibition Faszination Spiegelwelten (fascinating mirror worlds),[2] and the following activities are based on some of the stations in the exhibition.

Mirror anamorphosis (photo from the exhibition)
Image courtesy of MAINS/HLFF

Anamorphosis provides an excellent opportunity to combine concepts from physics, mathematics, geography, and art in an engaging way. These activities use cylindrical mirrors to provide examples for exploring optics with curved mirrors (Activity 1) and coordinate transformation and geometry (Activity 2), with a final activity to engage students in creating their own anamorphic visual art (Activity 3). More complicated topics for advanced students are also suggested.

Making cylindrical mirrors

All of the activities require the use of a cylindrical mirror (ideally one per group of students) that is around 15–20 cm high. The images provided in the supporting material for printing are optimised for a mirror that is 17 cm in circumference (around 5.4 cm in diameter), but other sizes can be used. You will just need to move the mirror closer or further away from the image to get a good result.

Cylindrical mirrors can be ordered from an education supplier, improvised from highly reflective metal tubes or pipes (e.g., from a DIY centre), or constructed using reflective film, as detailed below.

Materials

  • Highly reflective plastic film like metallized polyethylene terephthalate – this is often sold as privacy/UV-blocking films for windows
  • An object that can act as a cylindrical support (e.g., a can, bottle, or cardboard tube; this is not essential if the film is stiff enough to hold a cylindrical shape).
  • Ruler
  • Whiteboard marker
  • Scissors/craft knife
  • Sticky tape or glue

Procedure

  1. Unroll a section of the film and roll it into a tube shape roughly 5.5 cm in diameter. If the film seems stiff enough to hold a cylindrical shape (in a double layer), you don’t necessarily need a support. However, a support will make the cylinders more stable and easier to use.
  2. For a support, you can make a tube of the correct size by rolling up an appropriately sized piece of thin cardboard. Otherwise, measure the height and circumference of your support. Do not use a support that is narrower than 5 cm in diameter or the reflected images will be difficult to see.
  3. No support: measure and mark out a rectangle on the reflective film measuring >34 cm in width × 15–20 cm in height and then measure and mark a smaller rectangle 17 cm long within it (so that the film overlaps in at least two layers all the way around when rolled.

Roll up the film so that the outside edge lines up with the 17 cm mark, and tape it to create a cylinder with a circumference of 17 cm.


With a support: measure and mark out a rectangle of reflective film that is approximately the height of the support and with a length at least 3 cm longer than the support circumference.

Roll the film around the support and tape or glue in place.

Activity 1: Discovering the magic of curved mirrors

Assuming students have a basic understanding of reflection on plane mirrors, this activity can be performed as an in-class demonstration by a teacher to introduce optics with a curved mirror. Students are encouraged to predict, observe, and explain what is happening using their base knowledge. The demonstration takes less than 5 minutes, and the discussion takes 10–20 minutes.

Conical mirror station in the exhibition
Image courtesy of MAINS/HLFF

Materials

Procedure

  1. Before the lesson: if using cylindrical mirrors with a diameter other than 17 cm, teachers should experiment to find the correct mirror placement and draw an appropriate circle on the images.
  2. If necessary, recap reflection, including the characteristics of reflection from a plane mirror and the law of reflection (the angle of reflection equals the angle of incidence).
A diagram illustrating the law of reflection.
Image: And1mu/Wikipedia, CC BY 4.0
  1. The teacher hands out the cylindrical mirror images and asks students to speculate on how these images might appear when placed next to a cylindrical mirror.
  2. Students are then instructed to place the cylindrical mirror over the circle mark on the images. This should reveal the image.
Metal cylinder reflecting the distorted image of a virus (left) and a butterfly (right) on a white background.
Images adapted using AnaMorph-It plus V1.2.0. Adenovirus image adapted from Thomas Splettstoesser/Wikipedia, CC BY 4.0. Butterfly image adapted from Rawpixel, Public Domain
  1. Students should then answer the questions on the Activity 1 worksheet:
    1. Which rules of reflection on a plane mirror do the students see still apply here, and which do not? Complete the table.
      2. Property of reflection from a flat surfaceAppliesDoes not apply
      The image is virtual.X
      The image is of the same size as the object.X
      The image is laterally inverted, meaning that images are not reversed from top to bottom, but are reversed from left to right.X
      The distance between the image obtained from the mirror is the same as the distance between the object from the mirror.X
      The angle of incidence and the angle of reflection are always equal.X
      The incident ray, the normal at the point, and the reflected ray all lie on the same plane.X
    2. Are all parts of the images distorted equally? If not, which show the greatest distortion?
      Answer: the image is distorted by the same amount, regardless of the viewing angle around the mirror; however, the more distant parts are distorted more, compared with the parts that are near the mirror.

  1. Have the students move the mirror closer to and further away from the image, and again answer the question are all parts of the images distorted equally?
  2. The students may observe that the images are compressed by these convex curved mirrors. Can they think of a practical application? Examples are hallway safety or security mirrors, where the use of convex mirrors provides a wider field of view.
Image: Random Retail/Flickr, CC BY 2.0
  1. Optional: try the conical mirror with the images for conical mirrors (with holes in the centre to place them over the cone). Note that, to see the image, one must align one’s eyes with the axis of the cone. Students can also try the cylindrical mirror on the images for conical mirrors and vice versa, to see that the anamorphic effect only works with the correct mirror.
Example picture for a conical mirror. Note that the circle part should be cut out and the picture placed over the conical mirror.
Image courtesy of MAINS/HLFF

Results and discussion

After working through the exercise, the students should discuss why they observed the results they did. If necessary, the teacher can unveil the magic behind the scenes, but older students may be able to work it out for themselves by drawing ray diagrams for a convex mirror.

Students should first understand that, locally, curved mirrors can be understood as behaving like plane mirrors, with each ray reflecting from the point it hits the mirror, as if that point was the plane that formed the tangent to the curve at that point. By drawing several light rays to a curved mirror and following their paths, students should be able to see how the image becomes distorted. The teacher may introduce the concept of focus, focal length, and so forth.

Diagram showing the basic parts of a convex mirror and the trajectories of light that fall on it.
Image adapted from WiredAlexandria/Wikipedia, CC BY 4.0

The teacher may also use computer simulations for illustration, for example, this ray optics simulation from PhyDemo or this concave and convex mirrors simulation from oPhysics.

An optical explanation for the conical mirror is rather complicated to draw. For further information, teachers can refer to https://anamorphicart.wordpress.com/2010/04/21/conical-mirror-anamorphoses/.

Activity 2: Coordinate systems

As a continuation of Activity 1, in this activity, coordinate transformation is briefly studied, with more advanced geometry as an optional addition. The experiment itself only takes a few minutes, but the discussion can take 10 minutes or much longer, depending on how much detail is discussed.

Note that, generally, coordinate transformation refers to a change of description, and the object remains the same. In this sense, imaging using a cylindrical mirror is not a true coordinate transformation but a geometric transformation, but the explanation here primarily serves to prepare for Activity 3, where the students transcribe a picture from one coordinate system to another.

Materials

Procedure

  1. The teacher invites students to consider how the images used in Activity 1 are made. How do we map the normal image to an image that is revealed by the mirror? The answer is based on different coordinate systems! A square grid is known as Cartesian coordinates, and the anamorphic images are transformed to a polar coordinate system.
  2. Students should place paper with polar coordinates under the cylindrical mirror. What do they observe?
Photo from the exhibition. Note how the image appears as a grid with straight lines in the cylindrical mirror.
Image courtesy of MAINS/HLFF
  1. When the cylindrical mirror is placed at the right distance, polar coordinates morph into Cartesian coordinates, creating a familiar grid. Half-circles become straight lines, and the radial lines become parallel and perpendicular to those originating from half-circles.
© Technorama; used with kind permission

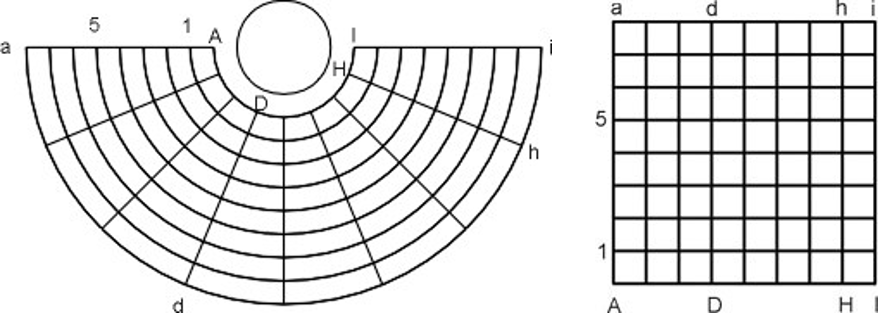
Remind the students of the question from Activity 2: are all parts of the images distorted equally? With the aid of a coordinate system, one can describe distances in unit length, allowing for a quantitative assessment of the degree of distortion.

  1. Advanced: what properties are preserved between the printed image and the reflection? Answer: the half-circles are ‘parallel’ (they never meet) to each other, and they remain parallel in the mirror image. The local perpendicular (the angle where the lines cross) is also preserved.
  2. The coordinate systems infosheet can be used to as a summary or for further discussion.

Discussion

These results can act as a basis for a discussion on geometric transformations or coordinate systems. The link to coordinate systems is particularly interesting since it links to the real-world problem of cartography.

Coordinate systems

A coordinate system is a method for identifying the location of a point. On a two-dimensional surface, coordinate systems use two numbers, a coordinate, to identify the location of a point. Each of these numbers indicates the distance between the point and some fixed reference point, called the origin.

A known example is the geographic coordinate system, which is the spherical coordinates of latitude and longitude.

The Cartesian, or rectangular, coordinate system consists of an origin, a horizontal x axis, and a vertical y axis. The point where the axes cross is the origin. Any point can be described by the horizontal distance from the y axis (x), and the vertical distance from the x axis (y); together these are written as (x, y). The origin is written as (0, 0). The coordinates can be read more conveniently with the help of a grid, where lines are drawn parallel to the axes.

For the polar system, only one axis and an origin are needed to define the measurement of distance and the reference direction. The coordinates are given by the distance from the origin (r), and the angle from the positive x axis (θ).

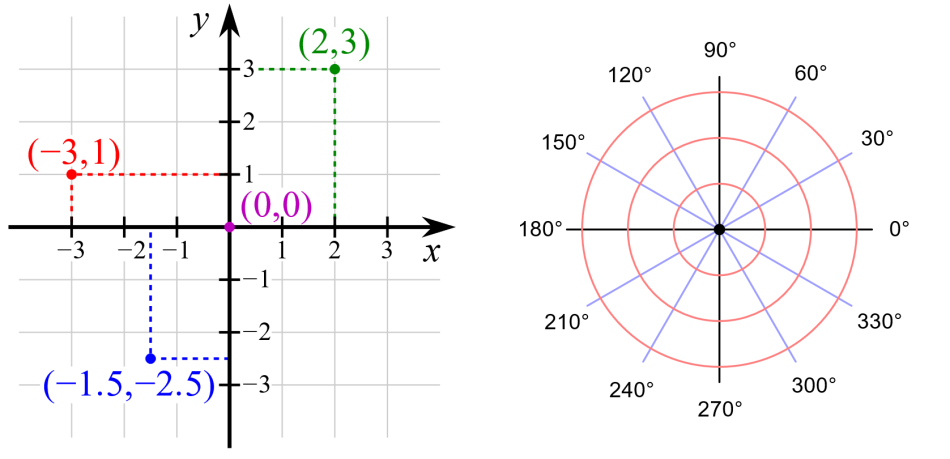
Cartesian coordinates (left) and polar coordinates (right)
Images: Cartesian coordinates: K. Bolino/Wikipedia, Public domain. Polar coordinates: Mets501/Wikipedia, CC BY SA 3.0

To convert from polar to Cartesian coordinates:

To convert from Cartesian to polar coordinates:

This kind of transformation, which involves preserving the angle but not lengths, is known as conformal mapping, a concept that is essential in mathematics and theoretical physics, and more practically, a technique employed in cartography to address the challenge of showing a curved planet on rectangular maps.

There are many different types of map projections and they all preserve different features of the globe, but no map from the sphere to the plane can be both conformal and area preserving; they all produce some kind of distortion. The best projection to use depends on the context.

This discussion can illuminate how common types of world map, like the Mercator projection, distort the true sizes of continents and oceans, thereby emphasizing the significance of understanding transformations. You can use thetruesize tool to explore how the Mercator projection distorts country sizes.

Activity 3: Become an artist

Armed with an understanding of coordinate transformations and the magic of curved mirrors, students are given the task of creating their own anamorphic artwork.

To add depth to this activity, the teacher can encourage students to consider other artistic implications of anamorphosis. How can they use these principles to create mind-bending illusions in their artwork? This activity not only reinforces the concepts learned but also sparks creativity and artistic expression.

This activity takes 30 minutes.

Tulip transformation: transcribing an image on a Cartesian grid to polar coordinates. The use of a curved mirror will reform the original image.
© Technorama; used with kind permission

Materials

Procedure

  1. Optional: show students examples of art, such as Holbein’s painting The Ambassadors, and let them know they can create their own anamorphic art in a relatively easy way – with the help of coordinate grids and curved mirrors. Otherwise, just explain that the coordinate systems discussed in Activity 2 can be used to create their own anamorphic images, as seen in Activity 1.
  2. Give them the tulip image to view with their mirrors. Explain how the coordinates allow you to transcribe any given point on one system to the other system. Show the tulip transformation sheet as an example.
  3. Give each student a set of polar and Cartesian coordinate papers (or whiteboards).
  4. The students should draw an image on the Cartesian coordinate system, and then attempt to transcribe it onto the polar system, exploring how the same image morphs and adapts to different transformations. The transcription will be much easier if they stick to whole or half squares on the Cartesian grid, with straight lines connecting points on the gridlines. Curves are much more difficult.
  5. They can draw the image in pencil first and check it with the curved mirror, before adding colour and viewing the final image.
  6. Optional: the teacher may encourage students to create other mirrors using reflective film and tape. They can then investigate how these mirrors distort objects in the classroom.

Optional extension activities

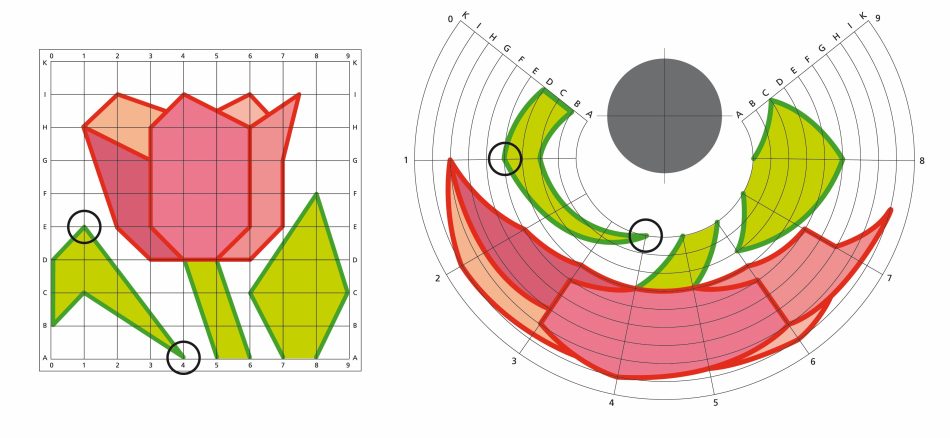
It is also possible to convert digital images to a polar coordinate system using software tools. This can be done in Photoshop using the ‘warp’ function (see the Photoshop instructions), although this gives only a simple semi-circular arc. A better alternative is the tool AnaMorph-It, which converts images to an optimal arc for use with a cylindrical mirror, and the free version can be used for creating and printing images. With these tools, students can create their own anamorphic images for cylindrical mirrors, using photos of their own artworks or other things that interest them.

The teacher may also encourage students to look up the artwork of M. C. Escher to explore other kinds of optical illusion, including impossible objects, in art.

Acknowledgements

The idea for this article originated from the exhibition The Fascinating World of Mirrors that was on display at MAINS in Heidelberg, Germany, in 2023. The exhibits were displayed in collaboration with the Science Center phaeno in Wolfsburg, Germany, where the exhibits, developed by Technorama, had been displayed previously.

MAINS was established by the Heidelberg Laureate Forum Foundation in 2017, with the goal of promoting awareness, interest, and understanding of mathematics and computer science by the public. Throughout the year, they offer various activities for all age groups, such as interactive exhibitions, an annual film festival, Science Notes, lectures, and workshops. They also offer guided tours of their exhibitions for school classes and groups.

References

[1] Faust M (2018) “Eyed awry”: blind spots and Memoria in the Zimmern Anamorphosis. Journal of Historians of Netherlandish Art 10. doi: 10.5092/jhna.2018.10.2.2

[2] Webpage of the exhibition Faszination Spiegelwelten (fascinating mirror worlds) on the MAINS website: https://www.heidelberg-mains.org/en/exhibitions/archive/the-fascinating-world-of-mirrors.html.

Resources

Author(s)

Yajie Liang is a master’s student at the Institute for Theoretical Physics in Heidelberg, where she studies cosmic structure formation and gravitational theories. She works at MAINS part time, where she gives tours through exhibitions in mathematics and computer science, and answers questions from visitors.

License

CC-BY
Text released under the Creative Commons CC-BY license. Images and supporting materials: please see individual descriptions.

Related articles

Teach

How much carbon is locked in that tree?

Biology, maths, and the SDGs: estimate the CO2 absorbed by a tree in the schoolyard and compare it to the CO2 emissions of a short-haul flight.

Earth science, Biology, Chemistry, Mathematics, Science and society, Sustainability