¿Puedo algo tener aceleración hacia arriba, mientras cae? Teach article
Traducido por Javier Aseguinolaza. Utilice uno de los más sorprendentes experimentos de la mecánica clásica para enseñar el método científico, el análisis de vídeo y la mecánica.
A veces, la mecánica clásica en la educación secundaria puede ser un reto para enseñar y aprender. La mayoría de los experimentos incluyen cosas como tirar de un bloque de madera a lo largo de una superficie plana con un medidor o muelle en escala de Newton, o dejar caer una pelota de tenis desde diferentes alturas – actividades que puede que ni sorprendan ni comprometan a los estudiantes a ningún nivel. Pero gracias a la rápida evolución de las cámaras de fotos de los teléfonos móviles, ahora se puede utilizar el análisis de vídeo para llevar a cabo investigaciones con facilidad, que hace unos años sólo podía hacerse en los mejores laboratorios de investigación. ¡Y el análisis detallado de los fenómenos aparentemente diarios puede conducir a veces a los resultados más sorprendentes!
Esta sugerencia como actividad de una lección es el resultado de tal investigación, realizada por un estudiante para un trabajo de un curso ordinario de física, en el cual los resultados sorprendieron por completo tanto al alumno como al profesor.
El experimento

Norrby
Un Slinky® es esencial en cualquier aula de Física. Se puede utilizar para muchas cosas, desde ilustrar ondas longitudinales hasta bajar las escaleras. Un Slinky tiene una propiedad sorprendente aún sólo relativamente bien conocida: si se sujeta desde arriba y se deja estirar bajo su peso propio, cuando se libera, la parte inferior del Slinky no se moverá hasta que el Slinky haya colapsado por completo (ver Figura 1). Muchos de los vídeos populares en línea muestran este interesante hechow1.
El proceso suele ser demasiado rápido para verlo a simple vista, pero se siente claramente si se coloca una mano justo debajo de la parte inferior del Slinky estirado antes de soltarlo. Puede demostrar fácilmente esta peculiar propiedad en el aula, preferentemente permitiendo que todos los estudiantes lo prueben manteniendo un Slinky con una mano y dejándolo caer sobre su otra mano.

bajo su propio peso y
liberado después
Imagen cortesía de Markus
Norrby
Después de presentar el fenómeno, puede plantear una pregunta de investigación: Si la aceleración de la parte inferior de la Slinky es cero, ¿cuál es la aceleración de la parte superior de la Slinky durante la caída?
El siguiente paso, según el método científico, sería establecer una hipótesis. Esto podría discutirse en el aula. Si el producto final deseado es un informe de laboratorio individual o de grupo, la hipótesis debería estar motivada por el razonamiento lógico y posibles referencias a literatura y debería ser escrito. En muchos casos, la hipótesis será que le aceleración de la parte superior del Slinky debería ser de alrededor de 2g o superior, para dar una aceleración media de g para todo el Slinky (al menos esa fue nuestra hipótesis cuando realizamos esta investigación por primera vez).
Para responder a la pregunta de la investigación, se debería utilizar el análisis de vídeo. Para un análisis detallado, la caída del Slinky necesita ser filmada a una velocidad mayor que la normal, al menos a 60 fotogramas por segundo y preferiblemente a 120 fotogramas por segundo, que puede lograrse con muchos de los smartphones más nuevos. Para reducir las incertidumbres, los estudiantes tienen que dedicar algún tiempo a la evaluación de los errores que podrían afectar los resultados del análisis de vídeo, como ángulo de la película, la posición de un objeto de tamaño conocido como referencia, y la resolución y velocidad del obturador de la cámara. A continuación se describe un modelo de procedimiento.
Materiales
Cada estudiante o grupo de estudiantes necesitará:
- Un Slinky
- Una regla métrica
- Un trípode
- Un dispositivo de grabación de vídeo (un smarphone o una cámara de vídeo)
- El software de análisis de vídeo (una gran herramienta gratuita es Trackerw2, herramienta de análisis de video y modelizado integrada en el entorno Open Source Physics Java. Utilizamos Pasco Capstonew3, herramienta comercial de adquisición de datos y análisis. Hay también aplicaciones móviles (apps) para realizar el análisis directamente en dispositivos móvilesw4)
Procedimiento
- Coloque la regla métrica verticalmente en una pared, con el inicio de la regla (por ejemplo: el extremo de 0 cm) en la parte superior.
- Colocar el trípode y la cámara tal que se pueda grabar la caída completa del Slinky.
- Mantenga el Slinky completamente extendido y alinee su extremo superior con el comienzo de la regla métrica.
- Comience a filmar.
- Suelte el Slinky.
- Detenga la filmación
- Si es necesario, importe el vídeo en el software de análisis correspondiente.
- El procedimiento exacto para el seguimiento del objeto de interés en el video varía ligeramente entre los diferentes tipos de software de análisis de vídeo. Los estudiantes deberían procesar el video para obtener datos que puedan ser representados en gráficos que muestren el tiempo respecto de la velocidad vectorial, el tiempo respecto de la velocidad media o el tiempo respecto de la aceleración.
- Analizar los resultados.
Puesto que la aceleración es elemento cuantitativo de interés en este caso, los estudiantes suelen comenzar por mirar el gráfico que muestra el tiempo respecto de la aceleración. Sin embargo, verán que sus valores están muy repartidos. Esta es una buena oportunidad de aprendizaje, para ayudar a los estudiantes a entender por qué los profesores de física persisten sobre la línea de mejor ajuste en diferentes diagramas.
Si los estudiantes analizan un gráfico que muestre el tiempo frente a la velocidad media o el tiempo frente a la velocidad vectorial, verán una curva mucho más suave y podrán obtener mejores resultados (véanse las figuras 2 y 3).
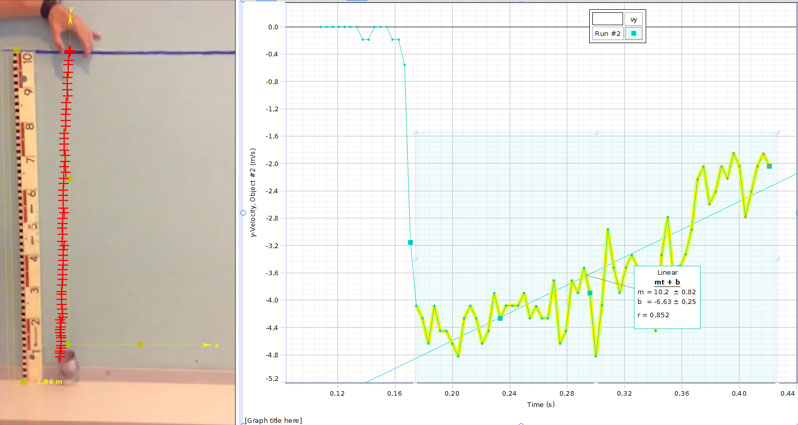
Imagen cortesía de Markus Norrby
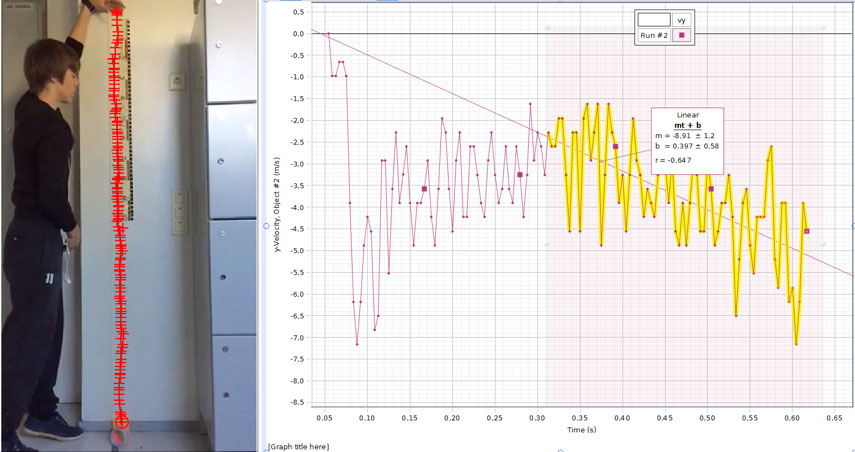
Imagen cortesía de Markus Norrby
Sobre lo que ocurre
La primera pregunta de investigación que se plantea cuando se realiza por primera vez el experimento es cómo están relacionadas la aceleración de la parte superior y la parte inferior del Slinky. Nuestra primera sorpresa después de ver el video a cámara lenta fue que la única parte del Slinky que se mueve, es la parte superior. Cada sección del Slinky por debajo de la parte superior se comporta como la parte inferior, colgando en el aire (casi) hasta ser golpeada por la parte superior.
La segunda, y aún más sorprendente, provino del análisis de la aceleración de la parte superior. Resulta que la parte superior del Slinky tiene una enorme aceleración en los primeros milisegundos en que se deja caer – por lo general alrededor de 200-300 m s-2 de media. Después de eso, la velocidad disminuye abruptamente, con un valor aparentemente constante para la aceleración de aproximadamente 10 m s-2. De hecho, habiendo repetido el experimento muchas veces, e incluyendo Slinkys de diferentes materiales y diámetros (ver figura 4), las barras de error de los resultados siempre incluyen el valor 9,8 m s-2, y el promedio se aproxima mucho al de un aceleración negativa de la gravedad.

probados por los autores
Imagen cortesía de Markus
Norrby
Una manera simple de convencerse de la validez del resultado es continuar el análisis un poco más allá, después de que el Slinky se haya colapsado completamente pero antes de que llegue al suelo. La aceleración del Slinky colapsado es, como era de esperar, igual a la aceleración de la gravedad. Observando la forma simétrica del gráfico del tiempo frente a la velocidad, es evidente que el signo de la aceleración cambia durante la caída de Slinky, pero que el módulo del valor permanece prácticamente igual (figura 3). La Figura 3 también muestra que la aceleración promedio total para todo el movimiento es de 9,8 m s-2, como cabría esperar.
Estos resultados deberían ser discutidos en el aula. Los estudiantes necesitan entender que no hay una explicación simple para este comportamiento; incluso los modelos más simples del fenómeno incluyen ecuaciones diferenciales y ondas propagadoras. Debe subrayarse la incertidumbre de los resultados, y el equipamiento profesional junto con un análisis en profundidad mostraría una estructura adicional en el comportamiento, como ocurre con la mayoría de los fenómenos de la vida real.
El problema de la caída del Slinky ha sido recientemente investigado con más detalle, y en los últimos años aparecen más y más referencias académicas cuando se busca en internet información sobre el tema. La explicación para la parte inferior que cuelga en el aire hasta que el Slinky ha colapsado es simple: la información sobre la parte superior del Slinky que se libera viaja como una onda a través del Slinky y tarda una cierta cantidad de tiempo en alcanzar el fondo. Pero otros aspectos son más difíciles de explicar.
El fenómeno fue investigado por Cross y Wheatland (2012), quienes hicieron un modelo semi-empírico para la caída del Slinky, suponiendo un tiempo de colapso finito de las vueltas detrás de una onda de propagación hacia abajo y comparando la distancia con imágenes de una cámara de alta velocidad.
Su análisis más detallado coincide con los resultados que los alumnos encontrarán arriba, pero los autores también observan una pequeña oscilación en la aceleración durante la caída. Su modelo, que predice una desaceleración no constante, no pudo ser probado de manera concluyente. En el artículo de Cross y Wheatland, los datos implican claramente una aceleración media para la fase de aceleración negativa de aproximadamente 10 m s-2, pero ello no se menciona en el artículo y no está apoyado directamente por el modelo.
Otros investigadores han intentado enfoquesw5 diferentes para modelizar la caída del Slinky, pero hasta ahora ningún modelo parece ser capaz de explicar completamente los detalles de este complicado movimiento. Por lo tanto, como dice el refrán: «Se necesita más investigación». Y mientras esperamos que la teoría de la física se ponga al día, podemos utilizar este fascinante experimento como inspiración para los estudiantes de física en toda Europa.
Esta es una oportunidad para que los profesores establezcan la conexión entre este experimento y muchos experimentos históricos en los cuales el resultado fue completamente inesperado. A menudo estos resultados imprevistos pueden hacer que la ciencia de un salto adelante, como el descubrimiento de Rutherford del núcleo atómico o el descubrimiento de Bequerel, de la radiactividad.
References
- Cross RC, Wheatland M S (2012) Modelizado de la caída del slinky. American Journal of Physics 80, 1051. http://dx.doi.org/10.1119/1.4750489. A preimpresión gratuita disponible en ArXiv at http://arxiv.org/pdf/1208.4629.pdf
Web References
- w1 – Mira un vídeo a cámara lenta de la caída de un Slinky, que también discute la ciencia involucrada.
- w2 – Descárgate y descubre más sobre el software de procesado de imágen Tracker.
- w3 – Descárgate el software comercial que usaron los autores, Pasco Capstone.
- w4 – Un ejemplo de una app para análisis de video Video Physics for iOS.
- w5 – Phil Gash, un professor de física de la Universidad Estatal de California, ha propuesto un modelo alternativo para la caída del Slinky.
Review
A medida que las cámaras de alta velocidad y las herramientas de análisis de vídeo son cada vez más disponibles, las aulas de física y laboratorios pueden aportar nuevas perspectivas en la investigación de muchos tipos de movimiento. El estudio de objetos que se mueven rápidamente o que cambian puede revelar aspectos muy interesantes y fascinantes.
El Slinky (un resorte helicoidal de acero o de plástico pre-comprimido) fue inventado como juguete. En este artículo, el estudio del movimiento que hace un estudiante y el comportamiento de un Slinky que cae, saca a la luz resultados inesperados y sorprendentes. Se puede continuar con más investigación y estudio de la fascinante conducta del Slinky en más aulas y laboratorios. ¡Y muchos más fenómenos podrían ser investigados por los estudiantes usando el análisis de video!
Vangelis Koltsakis, Grecia





