Supporting materials
Acelerómetros de muelle (Word)
Download
Download this article as a PDF

Traducido por Mª Fabiola Lacueva Pérez. Montañas rusas, carruseles y demás atracciones de feria no sólo pueden ser muy divertidas, sino que también pueden ser útiles para la clase de ciencias como propone Giovanni Pezzi.

Un parque de atracciones o una feria pueden ser el lugar idóneo para llevar a cabo experimentos de física irrealizables en un aula. En todo el mundo, diversos proyectos han elaborado actividades con este propósito (ver ‘Recursos’).
Una de estos es ‘Mirabilandia, un’aula senza pareti’ (“Mirabilandia, un aula sin paredes”), un proyecto italiano, iniciado en 2002 por profesores del centro de secundaria Liceo Torricelli en Faenza, en su parque de atracciones local, Mirabilandiaw1. La iniciativa fue tan exitosa que los responsables del parque decidieron ofrecerla a todos los centros educativos, realizando recorridos guiados por estudiantes de ciencias entrenados para ello.
¿Quizá podría proponerle al parque de atracciones de su localidad un proyecto similar? Entre tanto, aquí se presentan algunas actividades adecuadas para cualquier parque o feria. Para algunas, es necesario averiguar previamente las características técnicas de las atracciones, ya sea a través del parque o a través de la red, por ejemplo mediante la “Roller Coaster Database” (Base de datos de montañas rusas)w2. Para subir los instrumentos de medida a las atracciones, atados a los tobillos de los estudiantes o a la estructura de la atracción, se necesita el permiso de los responsables del parque. En nuestro caso, nuestro director habló con el gerente del parque, detallándole el proyecto que teníamos en mente.

Las actividades son adecuadas para alumnos de entre 15 y 19 años, pero se pueden adaptar para estudiantes más jóvenes. Abordan temas relativos al movimiento rectilíneo y al circular, velocidad y aceleración, las tres leyes del movimiento, gravedad, fuerzas centrípeta y centrífuga y transformaciones de energía.
Los estudiantes deberían estar familiarizados con los conceptos básicos de Cinemática y Dinámica, y necesitarán una introducción básica a las actividades antes de visitar el parque.
La tarea relativa a cada atracción requiere en torno a una hora, tiempo que pude incrementarse si es necesario hacer fila. Un equipo puede medir a bordo, mientras los otros trabajan en tierra. Normalmente no hay tiempo para que cada grupo repita las medidas, pero se pueden comparar los datos de distintos equipos. En el parque se puede realizar un análisis preliminar de los datos y continuarlo de vuelta en el aula.
En Mirabilandia, los estudiantes recibieron un cuadernillo para completar. Parte de éste se ha traducido al español y se puede descargarw3.

Dibuja un esquema del perfil vertical de la montaña rusa y discute las transformaciones de energía que se producen a lo largo del recorrido de las vagonetas, especialmente en el primer descenso y en los giros verticales.
En lo alto de la montaña rusa, antes del primer descenso, la energía potencial gravitatoria es máxima; durante el descenso, que suele tener una trayectoria parabólica en la que los pasajeros pueden experimentar ingravidez durante unos pocos segundos (en un caso ideal sin rozamiento, la componente vertical de la aceleración aumenta con la constante g como en un caída libre), ésta se transforma en energía cinética.
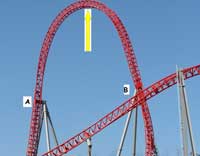
Utiliza los giros verticales para comparar la gravedad con la fuerza centrífuga. Los giros tienen forma de gota, siguiendo el camino de una espiral de Cornu o de Euler, en la que el radio de curvatura es inversamente proporcional a la distancia al centro, y por lo tanto se reduce la aceleración centrípeta, predominante en el giro, haciéndolo más confortable para los pasajeros.
Realmente sólo puedes apreciar la rapidez a la que se mueve una montaña rusa determinando su velocidad:
a) Calcula la velocidad instantánea dividiendo la longitud del tren de la montaña rusa entre el tiempo que le cuesta a todo el tren pasar por un punto determinado del recorrido.
b) Para obtener la velocidad media del tren a lo largo de una zona del recorrido de la montaña rusa, elige una que se observe fácilmente y de forma sencilla. Cuenta el número de traviesas (barras entre los raíles regularmente espaciadas) en esa zona y réstale una unidad para obtener el número de intérvalos. Mide cuánto le cuesta al tren recorrer la zona del recorrido elegida. Para calcular la distancia, multiplica el número de intérvalos entre su longitud (distancia entre dos traviesas). Divide esto entre el tiempo.
Comparar la velocidad instantánea registrada al final del primer descenso (el más rápido) con la velocidad calculada para un cuerpo en caída libre: v = √(2 g h) donde v: velocidad, g: aceleración de la gravedad, h: altura.

La velocidad medida debería ser menor, debido al rozamiento.
Presta atención a las sensaciones de ligereza y pesadez (aceleración) que se pueden experimentar en ciertos tramos del recorrido. Es posible obtener datos más precisos utilizando acelerómetros de muelle, o instrumentos portátiles más complejosw4. En la sección de recursosw3 están disponibles las instrucciones para construir y/o obtener estos instrumentos así como para evaluar los resultados.
Recientemente, se han popularizado teléfonos móviles (smart phones) dotados con acelerómetros de tres ejes. Las aplicaciones de estos dispositivos permiten dibujar gráficas de aceleración frente al tiempo o medir ángulos de inclinación.

Las torres de caída son estructuras verticales que los pasajeros recorren, arriba y abajo, sentados en una góndola. La góndola, o bien, se deja caer en caída libre; o bien, es empujada hacia arriba o hacia abajo con una fuerza superior a la gravitatoria.
Desde el suelo, se puede calcular la velocidad media de la góndola midiendo el tiempo de descenso con un cronómetro y dividiéndolo entre la altura de la torre. Ésta se pude comparar con la velocidad instantánea, utilizando un transportador y trigonometría básica o geometría. En la sección de recursosw3están disponibles las instrucciones detalladas para ser descargadas.

Durante el recorrido, se puede sentir la aceleración en tu cuerpo y medirla con instrumentos electrónicos portátilesw4.
En las torres en las que la góndola es impulsada hacia arriba, la aceleración puede alcanzar valores de hasta tres veces la gravitatoria.
Si se lleva un recipiente de plástico durante el viaje en la torre, se observa que durante la caída libre, el agua no se derrama, pero si la góndola es impulsada hacia abajo en vez de caer, sube el nivel de agua en el recipiente. Otra posibilidad es atarse a la muñeca una pequeña bola de goma (perforar la bola para anclar el muelle) y situarla sobre la palma de la mano.

Las siguientes actividades también son adecuadas para estudiantes más jóvenes, de edades comprendidas entre 11 y 14 años. Deberían estar familiarizados con los conceptos de velocidad y presión atmosférica, y aprenderán sobre movimiento circular uniforme (tiempo, velocidad, frecuencia) y utilizarán sus conocimientos sobre presión atmosférica. Tanto en tierra como durante el recorrido, medir y anotar el tiempo tras un cuarto de vuelta, media vuelta, tres cuartos de vuelta y una vuelta completa de la noria.

Los estudiantes deberían averiguar que el tiempo empleado en cada cuarto de vuelta es similar, y por lo tanto que el movimiento de la noria es regular y la velocidad constante.
Calcular la distancia recorrida por la góndola (a partir del radio de la noria), su velocidad media, y, como un ejercicio de matemáticas aplicadas al mundo real, el ángulo en el centro de la noria entre las dos barras que conectan dos góndolas contiguas con el centro (dividir 360º entre el número de góndolas).
Se puede determinar la altura de la noria del mismo modo que en la torre de caída (ver arriba) o utilizando un barómetro electrónico para determinar el cambio en la presión atmosférica durante el viaje en noria.
Cada 0,1 kPa de cambio en la presión corresponde aproximadamente a un cambio de unos 8 m en la altitud. En internetw5. está disponible una descripción más precisa de la relación entre altitud y presión. Comparar los resultados y discutir sobre las ventajas y desventajas de cada método (exactitud, instrumentos, tiempo y esfuerzos invertidos).

Un tiovivo es el lugar perfecto para estudiar el péndulo de Foucault y el efecto de Coriolis. Los estudiantes deberían estar familiarizados con el movimiento del péndulo, la gravedad, las fuerzas centrípeta/centrífuga, y la rotación. Los detalles sobre cómo realizar los experimentos se pueden conseguir en internetw3.
Cada año al comienzo de septiembre, Mirabilandia presenta a los profesores sus recorridos educativos con una jornada de puertas abiertas. Consultar: www.mirabilandia.it/#/scuole
Alberghi S et al. (2007) Is it more thrilling to ride at the front or the back of a roller coaster? The Physics Teacher 45(9): 536-541. The article is freely available online.
Bakken C (2011) Amusement Park Physics. College Park, MD, USA: American Association of Physics Teachers. ISBN: 9781931024129
Unterman NA (2001) Amusement Park Physics: A Teacher’s Guide. Portland, ME, USA: J Weston Walch. ISBN: 9780825142642
Estos profesores italianos han hallado un modo innovador y admirable para sacar la Física fuera del aula. En su útil artículo, las actividades están descritas claramente, haciéndolas fácilmente reproducibles. Los conocimientos necesarios para realizarlas se pueden tratar fácilmente durante las clases habituales; prevé tiempo para la preparación de instrumentos y libros de actividades.
El artículo también aborda la seguridad en los parques de atracciones, lo cual requiere una planificación cuidadosa. Quizás podrías evaluar tus habilidades ingenieriles construyendo tu propia montaña rusa virtual (utilizando www.learner.org/interactives/parkphysics) y valorando su seguridad El artículo también proporciona enlaces a otros sitios web útiles.
Para los estudiantes más jóvenes (de edades comprendidas entre 13 y 16), el artículo se puede utilizar para estudiar el movimiento rectilíneo; las tres leyes del movimiento; gravedad; y transformaciones de energía. Los estudiantes de más de 16 años también podrían estudiar estos temas con mayor detalle, junto con el movimiento circular, las fuerzas centrífuga y centrípeta. [Nótese que el autor sugiere realizar estas actividades con estudiantes de entre 15 y 19 años de edad.]
Catherine Cutajar, Malta
Acelerómetros de muelle (Word)
Download this article as a PDF