Supporting materials
Download
Download this article as a PDF

Tradotto da Giovanni Pezzi. Gli ottovolanti, i Carousel e altre attrazioni dei parchi di divertimento possono essere non solo un momento di divertimento, ma anche l’occasione per una lezione scientifica, come ci spiega Giovanni Pezzi.

Un parco di divertimenti o un luna park sono posti ideali per realizzare esperimenti di fisica che non potrebbero mai essere svolti in classe. Molti progetti nel mondo hanno sviluppato attività didattiche da svolgere nei parchi (vedi ‘Fonti’).
Uno di questi è “Mirabilandia, un’aula senza pareti”, un progetto italiano partito nel 2002 per iniziativa di alcuni insegnanti del Liceo “Torricelli” di Faenza, realizzato nel vicino parco di divertimenti di Mirabilandiaw1. L’iniziativa ebbe un successo così ampio che la direzione del parco decise di renderlo disponibile per tutte le scuole, offrendo percorsi didattici guidati da tutor oppositamente formati.
Non sarebbe una buona idea proporre una simile iniziativa al tuo parco di divertimenti più vicino? Nel frattempo, ecco qui alcune attività adatte per qualsiasi parco di divertimenti o luna park. Per alcune sarà necessario procurarsi prima le informazioni tecniche relative alle attrazioni, o direttamente dal parco oppure on line, ad esempio utilizzando il data base dei ottovolantiw2. Per effettuare misure a bordo delle attrazioni occorre chiedere l’autorizzazione della direzione; gli strumenti possono essere fissati in modo sicuro alla struttura dell’attrazione o al polso dei ragazzi. Nel nostro caso, il Dirigente della scuola aveva contattato la direzione del parco spiegando in dettaglio il progetto che intendevamo realizzare.

Le attività sono rivolte a ragazzi di età 15-19 anni, ma possono essere riadattate anche per studenti più giovani. Gli argomenti riguardano il moto rettilineo e circolare, la velocità e l’accelerazione, le tre leggi della dinamica, la gravità, le forze centripete e centrifughe, le trasformazioni energetiche.
Gli studenti devono avere le conoscenze di base dei concetti principali di cinematica e dinamica ed è opportuna una presentazione delle attività prima della visita al parco.
Le attività su ciascuna attrazione richiedono circa un’ora di tempo, ma a volte le file di attesa per salire sulle attrazioni possono dilatare i tempi programmati. Mentre un gruppo di studenti effettua le misure a bordo, un altro svolge attività a terra. Di solito non c’è tempo per ripetere le misure, ma possono essere confrontati i dati presi da diversi gruppi. Una prima analisi dei dati può essere effettuata subito al parco e poi continuata in classe.
A Mirabilandia gli studenti ricevono un quaderno di lavoro da compilare. Alcune sue pagine possono essere scaricatew3.

Tracciare uno schema bidimensionale del profilo in altezza del ottovolante e discutere le trasformazioni energetiche lungo il tracciato, in particolare nella prima discesa e nei loop verticali.
In cima al ottovolante, prima della prima discesa, l’energia potenziale gravitazionale ha il valore massimo; viene trasformata in energia cinetica lungo la discesa, che spesso ha un profilo parabolico, e dove i passeggeri possono provare per pochi secondi la sensazione di assenza di peso (nel caso ideale di assenza di attriti, per effetto della gravità la componente verticale del moto è uniformemente accelerata, con accelerazione g, come nella caduta libera).
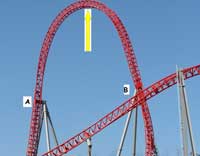
Sfruttare i loop verticali per discutere il ruolo della forza di gravità e della forza centrifuga. I loop sono a forma di goccia, e il profilo del percorso segue una curva chiamata clotoide, in cui il raggio di curvatura è inversamente proporzionale alla distanza dal centro. Questo permette di sottoporre i passeggeri, nel loop, ad accelerazioni centripete più confortevoli.
Per capire quanto si muove rapidamente un ottovolante è necessario calcolarne la velocità:
a) Si calcola la velocità istantanea dividendo la lunghezza del treno del ottovolante per il tempo impiegato, dall’intero treno, a passare davanti a un punto determinato dell’attrazione.
b) Per calcolare la velocità media del treno lungo una sezione del percorso, è bene scegliere una parte che sia facile da vedere e di forma semplice. Si conta il numero di traversine (cioè le barre equidistanziate tra i binari) che ci sono in quella sezione, e sottraendo uno si ottiene il numero di intervalli. Si cronometra il tempo richiesto dal treno a passare lungo quella sezione. Per calcolare la distanza percorsa, si moltiplica il numero degli intervalli per la lunghezza di ogni intervallo (la distanza tra le traversine). Si divide questo per il tempo misurato.
Confrontare la velocità istantanea misurata alla fine della prima discesa (la più veloce) con quella calcolata per un corpo in caduta libera: v = √(2 g h), dove v: velocità, g: accelerazione di gravità, h: altezza.

La velocità misurata dovrebbe risultare più bassa, per via dell’attrito.
Prestare attenzione alla sensazione di leggerezza o di pesantezza (accelerazione) che si può provare a bordo in alcune sezioni dell’attrazione. Dati più accurati possono essere ottenuti con accelerometri a molla o con più complessi strumenti portatiliw4. Istruzioni per costruire o procurarsi questi dispositivi e analizzare i risultati possono essere scaricati nella sezione Fontiw3.
Negli ultimi tempi si sono abbastanza diffusi telefoni cellulari che hanno incorporato un accelerometro a tre assi. Ci sono applicazioni per questi telefoni che permettono di tracciare grafici dell’accelerazione in funzione del tempo o di misurare l’angolo di inclinazione.

Le torri di caduta sono strutture verticali su cui i passeggeri si muovono verso l’alto o verso il basso, seduti su seggiolini o cabine. In un tipo, il seggiolino è lasciato andare in caduta libera, in un altro viene spinto con una forza maggiore di quella di gravità.
Da terra si può calcolare la velocità media del seggiolino o della cabina cronometrando il tempo di discesa e dividendo per l’altezza della torre. Il risultato ottenuto può essere confrontato con la velocità istantanea di un corpo in caduta libera. Per misurare l’altezza della torre, si può usare un goniometro e applicare nozioni di base di trigonometria o di geometria. Istruzioni dettagliate possono essere scaricate dal sitow3.

A bordo, durante il lancio, si può avvertire l’accelerazione sul proprio corpo e misurarla con strumenti elettronici portatiliw4.
Sulle torri dove i seggiolini sono spinti verso il basso, si raggiungono accelerazioni che sono il doppio o il triplo di quella di gravità.
Se si sale a bordo con un bicchiere di plastica pieno d’acqua, si può osservare che, nel caso della caduta libera, l’acqua rimane dentro il bicchiere, mentre nel caso in cui il seggiolino è spinto verso il basso con accelerazione maggiore di quella di gravità, il livello dell’acqua nel bicchiere cresce. In alternativa, si può tenere sul palmo della mano una pallina di gomma legata al polso (forare la pallina per attaccarvi la corda),

Le seguenti attività sono adatte per studenti più giovani, età 11-14 anni. Devono possedere conoscenze di base relative ai concetti di velocità e di pressione atmosferica. L’attività coinvolge il moto circolare uniforme (tempo, velocità, frequenza) e applicazioni della pressione atmosferica. Sia a terra che a bordo si misura e si prende nota del tempo dopo un quarto di giro, mezzo giro, tre quarti di giro, un giro completo della ruota.

Gli studenti dovrebbero scoprire che il tempo impiegato per ogni quarto di giro è lo stesso, per cui il moto della ruota è regolare e la velocità è costante.
Si calcola la lunghezza del percorso della cabina (conoscendo il raggio della ruota), la sua velocità media, e, come applicazione della matematica al mondo reale, l’angolo formato al centro della ruota dalle barre che sostengono due cabine vicine (si divide 360° per il numero delle cabine).
Si può determinare l’altezza della ruota con lo stesso metodo usato per le torri di caduta (vedi sopra) o usando un barometro elettronico per misurare la variazione della pressione atmosferica durante la rotazione.
Ogni 0,1 kPa di variazione di pressione corrisponde a circa 8 metri di variazione di altitudine. Una più accurata descrizione della relazione tra pressione e altitudine è disponibile onlinew5. Si confrontano i risultati e si discutono vantaggi e svantaggi di ciascun metodo (accuratezza, strumenti, tempo e impegno richiesti).

Un Carousel è il luogo ideale per studiare il pendolo di Foucault e l’effetto della forza di Coriolis. Gli studenti devono avere conoscenze di base in merito al moto del pendolo, alle leggi del moto, la gravità, le forze centripete / centrifughe, la rotazione. Si possono scaricare dal sito i dettagli su come realizzare questi esperimentiw3.
Ogni anno all’inizio di Settembre Mirabilandia presenta i suoi progetti didattici all’interno di un Convegno rivolto agli insegnanti; vedi: www.mirabilandia.it/#/scuole
Alberghi S et al. (2007) Is it more thrilling to ride at the front or the back of a roller coaster? The Physics Teacher 45(9): 536-541. The article is freely available online.
Bakken C (2011) Amusement Park Physics. College Park, MD, USA: American Association of Physics Teachers. ISBN: 9781931024129
Unterman NA (2001) Amusement Park Physics: A Teacher’s Guide. Portland, ME, USA: J Weston Walch. ISBN: 9780825142642
Questi insegnanti italiani hanno scoperto un modo sicuramente innovativo ed efficace per portare la fisica fuori della classe. In questo articolo, veramente utile, le attività sono spiegate con chiarezza, rendendo semplice la loro riproduzione. Le conoscenze di base richieste per sviluppare le attività possono facilmente essere svolte durante le normali lezioni; prevedere un certo tempo per preparare gli strumenti e i quaderni di lavoro.
L’articolo inoltre illustra i problemi della sicurezza nei parchi di divertimento, che richiedono un’attenta progettazione. Forse potreste mettere alla prova le vostre capacità ingegneristiche costruendo il vostro ottovolante virtuale (usando www.learner.org/interactives/parkphysics) e testandolo per la sicurezza. L’articolo inoltre contiene molti collegamenti utili a siti web.
Con gli studenti più giovani (età 13-16 anni) l’articolo potrebbe essere usato per affrontare il moto rettilineo, la velocità e l’accelerazione; le tre leggi del moto; la gravità; le trasformazioni energetiche. Gli studenti di età maggiore di 16 anni potrebbero esaminare questi argomenti in maggior dettaglio, insieme con il moto circolare, la forza centripeta e centrifuga. [L’autore suggerisce di realizzare le attività con studenti di età 15-19 anni]
Catherine Cutajar, Malta
Download this article as a PDF