The ALMA Observatory: the sky is only one step away Understand article
Claudia Mignone and Douglas Pierce-Price take us on a trip to the Chilean Andes, to the site of ALMA, the world’s largest radio astronomy facility, which is set to discover the secrets of our cosmic origins.

Chajnantor plateau in late
2009
Image courtesy of ALMA
(ESO / NAOJ / NRAO)
Imagine hiking in the Atacama region, high in the Andes of northern Chile, one of the driest and remotest spots on Earth. At altitudes of 5000 m and higher, life is not easy here: the atmospheric pressure is much lower than at sea level, and oxygen is scarce.
The landscape, dominated by large volcanoes and other mountain peaks, occasionally decorated by salt flats and picturesque formations of ice and snow, hardly resembles a typical view of our planet. Then, in the midst of this arid and abandoned region, you become aware of a gigantic construction – could those be huge satellite dishes?
Not exactly. This is the Atacama Large Millimeter/submillimeter Array (ALMA), an ensemble of huge, high-precision antennas that is currently being built on the Chajnantor plateau by an international partnership between Europe, North America and East Asia in cooperation with the Republic of Chile. The European partner in ALMA is the European Southern Observatory (ESO). ALMA is a revolutionary observatory which, when complete in around 2012, will allow astronomers to observe the light coming from some of the coldest and most distant objects in the Universe, with much better resolution and sensitivity than is presently possible.
ALMA is the largest ground-based astronomy project in existence. Three antennas have already been installed – an impressive enterprise given the challenging conditions of the site. However, those who visit the Chajnantor plateau a couple of years from now will encounter 66 antennas, 54 of which will have 12 m diameter dishes, and 12 smaller ones, with a diameter of 7 m each.
The most visible part of each antenna is the dish, a large reflecting surface. The dish is what lenses and mirrors are to ‘traditional’, or optical, telescopes: it collects radiation coming from distant astronomical objects, and focuses it into a detector which measures the radiation. The difference between the two types of telescopes is the wavelength of the radiation detected. Visible light, captured by optical telescopes, is just a small part of the spectrum of electromagnetic radiation (see box), with wavelengths between 380 and 750 nm (millionths of a millimetre). ALMA, in contrast, will probe the sky for radiation at longer wavelengths from a few hundred micrometres to about 1 mm. This is known as millimetre and submillimetre radiation, a subset of radio waves.

prototype for ALMA
Image courtesy of ESO
ALMA’s dishes differ from the mirrors of a visible-light telescope in both smoothness and size. The reflecting surfaces of any telescope must be virtually perfect: if they have any defects that are larger than a few per cent of the wavelength to be detected, the telescope will not produce accurate measurements. The longer wavelength to be detected by ALMA’s antennas means that although they are accurate to much less than the thickness of a single sheet of paper, the dishes do not need the mirror finish used for visible-light telescopes. So although ALMA’s dishes look like giant metallic satellite dishes, to a (sub)millimetre-wavelength photon, they are still almost perfectly smooth reflecting surfaces, focusing the photons with great precision.
The resolution (or degree of detail in the image) of a telescope depends both on the wavelength at which it operates and on the size of its aperture – the diameter of the main dish or mirror. The longer the wavelength, the worse the resolution; and the larger the diameter, the better the resolution. The relationship between the angular size of the smallest details that can be distinguished (θ), the wavelength (λ) and the diameter (D) is given by: θ ≈ λ/D. Note that small θ (angle) values represent finer details and hence better resolution. Consequently, a (long-wavelength) radio telescope with the same-sized dish as a (short-wavelength) visible-light telescope would have a worse resolution.
Therefore, to achieve a resolution comparable with that of state-of-the-art visible-light telescopes, a radio telescope like ALMA would need a reflecting surface with a diameter of a few kilometres – clearly unfeasible. This is why ALMA consists of an array of many individual antennas spread out over a very large area, working together in what is known as an interferometer.
The resolution of an interferometer is given by θ ≈ λ/B, where θ is the resolution, λ the wavelength and B the maximum baseline, the separation between a pair of antennas in the array. In other words, an interferometer acts like a single telescope as large as the whole array.
Increasing the maximum distance between the antennas increases the resolving power of the interferometer, allowing it to detect smaller details. The ability to link antennas over baselines of many kilometres is crucial to obtain extremely good resolution and a high degree of detail in the images.
ALMA’s main array will have fifty 12 m antennas, arranged in configurations spread over distances from 150 m to 16 km. The array will thus simulate a giant, single telescope much larger than any that could actually be built. In fact, ALMA will have a maximum resolution which is even better than that achieved at optical wavelengths by the Hubble Space Telescope.

Image courtesy of ALMA (ESO / NAOJ / NRAO) / L Calçada
The remaining four 12 m antennas and the twelve 7 m antennas will form the Atacama Compact Array. The smaller 7 m antennas can be clustered more closely together; because of the way interferometers behave, this compact arrangement allows them to see the broader structure or ‘big picture’ of the astronomical objects that are observed. In addition, the four 12 m antennas will be used separately to measure the absolute brightness of the objects observed, which is a quantity that cannot be measured with an interferometer.
The different configurations of the telescope allow astronomers to probe both the broad structure of an astronomical source and its very finest details. However, to switch between compact and wide configurations of the array, the antennas must be physically moved. This is done with two custom-built transporters, designed to lift the antennas, which each weigh more than 100 tonnes, move them kilometres across the desert, and position them on concrete docking pads with millimetre precision.
One of the goals of ALMA is to capture radiation from very distant galaxies: they were among the first to form in the history of the Universe, and we see the light that they emitted over ten billion years ago. The wavelength of the light emitted by these remote galaxies is ‘stretched’ as it travels toward us, because the Universe is expanding: what starts as infrared light eventually reaches Earth with millimetre or submillimetre wavelengths. This makes a telescope like ALMA the ideal tool to hunt for the very first galaxies and explore how structure formed in the Universe.

Image courtesy of ESO / WFI (optical); MPIfR / ESO / APEX / A Weiss et al. (submillimetre); NASA / CXC /CfA / R Kraft et al. (X-ray)
ALMA will also explore in unprecedented detail many stellar nurseries – the vast, cold clouds of gas and cosmic dust grains in interstellar space where new stars are born. The light produced by these young stars is absorbed and re-emitted, at longer infrared and (sub)millimetre wavelengths, by the dust. Observed through an optical telescope, these regions are often obscured by the dust grains and therefore dark, but they shine brightly in the (sub)millimetre part of the spectrum. ALMA will be the most powerful telescope for observing these extremely cold clouds, and it will deliver images of them with an unprecedented degree of detail. Thanks to ALMA, astronomers will be able to make detailed images of stars and planets being born in gas clouds near our Solar System and to better understand how stars, planetary systems and even life itself formed.

Image courtesy of ESO / APEX / DSS2 / SuperCosmos / Deharveng (LAM) / Zavagno (LAM)
(Sub)millimetre radiation, therefore, opens a window onto the cold and the distant Universe, but it is very challenging to detect because it is heavily absorbed by the water vapour in the Earth’s atmosphere. For this reason, telescopes for this kind of astronomy must be built on high and dry sites, where the atmosphere is rarefied and its water vapour content minimal. This is why the Chajnantor plateau at 5000 m altitude, one of the driest places on Earth, was chosen for ALMA. Here, astronomers will enjoy unsurpassed conditions for observing the Universe, but the price to pay is high, as they must operate a frontier observatory under very difficult conditions. Working at these high altitudes, the astronomers will be exposed to the same problems that mountaineers experience, such as altitude sickness, low atmospheric pressure and lack of oxygen to breathe. To make technical operations and everyday work easier, a base camp has been built at a lower altitude of about 2900 m. In short, if a site is good for (sub)millimetre astronomy, you most certainly do not want to live there.
Although the village of San Pedro de Atacama is located just some 50 km away, walking around the ALMA site feels almost like visiting another planet. The plateau of Chajnantor is so high up that the frantic routine of urban life is but a pale memory, and this helps make it a unique location on Earth to explore the hidden and distant mysteries of the cosmos. From here, space is just one step away.
Detecting astronomical objects along the electromagnetic spectrum
Visible light is just a small part of the whole spectrum of electromagnetic radiation. The different parts of the spectrum, or spectral bands, are, in order of decreasing wavelength and increasing frequency: radio waves (including microwaves and (sub)millimetre radiation), infrared, visible, ultraviolet, X-rays and gamma rays.
Because different physical processes in the Universe emit light at different wavelengths, each class of objects in the Universe shines most brightly in one or several particular spectral bands. Modern astronomers often try to target many bands, using different telescopes, since each set of observations provides a complementary piece of the puzzle; this approach is called multi-wavelength astronomy.
However, Earth’s atmosphere complicates matters, because it absorbs most of the radiation. Although this protects us, it makes life difficult for astronomers: only a tiny fraction of the electromagnetic spectrum is observable from the ground, and often in these cases, the quality of the observations strongly depends on the geographical site. This is why choosing an excellent site such as Chajnantor for ALMA is so important. In other spectral bands, especially at very short wavelengths, astronomers need telescopes aboard satellites in orbit around our planet, outside the obscuring layer of the atmosphere.
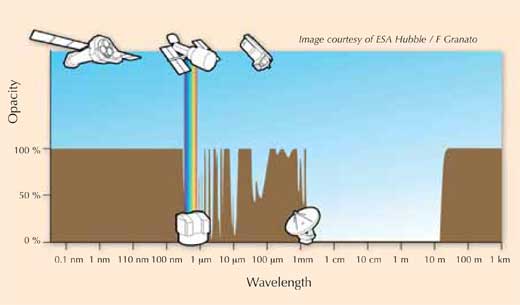
Image courtesy of ESA / Hubble / F Granato
Resources
- The website of In Search of our Cosmic Origins, a planetarium show about ALMA, provides teachers and educators with a series of worksheets, including detailed information and practical exercises about the scientific and technical topics presented in the article. See: www.cosmicorigins.org and www.cosmicorigins.org/education.php
- For more information about ALMA, see www.eso.org/alma and www.almaobservatory.org
- To watch ESO’s video podcast about ALMA, see: www.eso.org/public/videos/eso0849b
- For a short video introduction to ALMA, see: www.eso.org/public/videos/almatrailer2009
- For more videos about ALMA, see: www.eso.org/public/videos/archive/category/alma
- To learn more about the Atacama region and how, as part of the ALMA project, the historical and environmental aspects of the region are being respected, see the ALMA website (www.almaobservatory.org) or use the direct links: http://tinyurl.com/ydg2usl and http://tinyurl.com/yamfh77
Institutions
Review
It is not uncommon for teachers to mention optical telescopes during physics lessons but references to telescopes that make use of other types of radiation are less common. This article is interesting as it gives an insight into an ongoing project to build a radio telescope.
Teachers would find this article particularly useful and applicable in a discussion about the resolving power of an instrument. Suitable comprehension questions include ‘Why do the antennas need to be spread out over a large area?’ and ‘Why can’t a single instrument be used?’
Paul Xuereb, Malta





