Odległości we wszechświecie Teach article

Tłumaczenie Ewa Stokłosa. W jaki sposób astronomowie mierzą odległości do gwiazd? Rejestracja paralaksy z pomocą cyfrowego aparatu to precyzyjna i autentyczna metoda, którą można wykorzystać podczas lekcji.

Astronomowie to obserwatorzy, których od badanych obiektów dzielą ogromne przestrzenie. Znajomość odległości, w jakiej znajdują się ciała niebieskie jest kluczowa: dostarcza najważniejszego czynnika do odróżniania bardzo jasnych, odległych obiektów od tych bliższych, ale z natury mniej jasnych – czyli do stwierdzenia, jaki jest obserwowany obiekt. Nawet pojedyncze gwiazdy i całe galaktyki mogą wyglądać podobnie – dopóki nie dowiemy się, że jedno znajduje się miliardy razy dalej od drugiego, czyli że w rzeczywistości jest biliony razy jaśniejsze.

Najważniejszą astronomiczną metodą ustalania odległości od Ziemi do gwiazd jest paralaksa – pozorne przesunięcie pozycji obserwowanego obiektu w momencie zmiany punktu obserwacji. Zjawisko paralaksy można zaobserwować jadąc pociągiem: najbliższe obiekty za oknem wydają się poruszać znacznie szybciej od dalszych. Dzięki paralaksie możemy ustalić odległość od obiektu mierząc pozorną zmianę jego pozycji przy zmianie punktu obserwacji.

Wyzwanie stanowi tu oczywiście precyzja. Jak możemy obliczyć odległość na podstawie paralaksy najprecyzyjniej jak to możliwe? W drugim artykule poświęconym pomiarom odległości przy pomocy paralaksy wykorzystamy autentyczną metodę bardzo podobną do tej, którą wykorzystują astronomowie i która została dostosowana do użytku lekcyjnego (zobacz poprzedni artykuł Pössel, 2017). Zamiast korzystać z przyrządów do mierzenia kątów (jak w poprzednim artykule opartym na pomiarach z teodolitem) aby obliczyć odległość do „gwiazdy”, teraz zrobimy zdjęcia z różnych pozycji i wykorzystamy je do obliczeń koniecznych przy wyznaczaniu odległości.

Inny rodzaj metody fotograficznej, opisany w dalszej części artykułu, jest jeszcze bardziej autentyczny i precyzyjny, choć nieco bardziej skomplikowany. Zakłada wykorzystanie nieruchomego punktu odniesienia poza salą – tak, jak astronomowie opierają się na odległych obiektach tła (np. aktywnych galaktykach zwanych kwazarami), czyli nieruchomych punktach odniesienia, gdy mierzą paralaksę gwiazd, zamiast na teleskopach skierowanych w ten sam punkt podczas każdej obserwacji.

Do ćwiczeń potrzebny będzie aparat cyfrowy zamocowany (jeśli istnieje taka możliwość) na ławie optycznej (zob. ryc. 1). Ćwiczenia mogą zostać wykonane przez uczniów w grupach. Poświęćcie 30 minut na przygotowania i pomiary i kolejne 30 minut na analizę oraz obliczenia.

Materiały

• Obiektyw aparatu cyfrowego o znanej ogniskowej (minimum 50 mm)
• Ława optyczna (lub podobna podpórka umożliwiająca przesuwanie aparatu na boki oraz pomiar tego przesunięcia, jak np. płaski blat i długa linijka)
• Model gwiazdy (mała kulka o średnicy nie większej niż 1 cm lub dioda LED umocowana na drążku)
• Obiekt o znanej, jasno oznaczonej długości (np. calówka), do wykorzystania przy kalibracji
• Taśma miernicza
• Program do przetwarzania obrazów, np. Adobe Photoshop, GIMP

Procedury

1. Umieść aparat na ławie optycznej w sposób, który umożliwia przesunięcie aparatu w bok o znany odcinek. Aparat powinien być skierowany prostopadle do długości ławy (ryc. 1). Jeśli nie masz ławy optycznej, przyklej długą linijkę taśmą do powierzchni blatu w taki sposób, aby móc przesuwać aparat wzdłuż niej i zmierzyć długość tego przesunięcia.
    

2. Model gwiazdy umieść na drążku w taki sposób, aby znajdowała się ona na poziomie aparatu i kilka metrów od ławy.
3. Przesuń aparat na jeden z końców ławy i upewnij się, że gwiazda jest w nim widoczna. Zrób zdjęcie gwiazdy z tej pozycji.
4. Następnie przesuń aparat wzdłuż ławy optycznej w taki sposób, aby gwiazda nadal była widoczna w obiektywie. Odnotuj, o jaki odcinek przesunięty został aparat, a następnie zrób kolejne zdjęcie z nowej pozycji.
5. Przesuń aparat na pozycję środkową. Teraz umieść przedmiot kalibrujący (np. calówkę) prostopadle do kąta widzenia aparatu i zrób jego zdjęcie. Będzie ono potrzebne do skalibrowania pomiarów.
6. Przy pomocy taśmy mierniczej odczytaj i zanotuj odległość od aparatu do calówki.

Pomiar odległości do gwiazdy

Eksperyment przedstawiony jest na rycinie 2. Tutaj b to długość przesunięcia wzdłuż podstawy aparatu (ławy optycznej lub blatu) pomiędzy pozycją pierwszą i drugą (A i B), C to miejsce, w którym znajduje się model gwiazdy, natomiast d to odległość od podstawy aparatu do gwiazdy – czyli wielkość, którą próbujemy obliczyć.

Obliczenia konieczne do wyznaczenia d podane są poniżej.

1. Jeśli narysujemy linię równoległą do podstawy i znajdującą się w takiej samej odległości d od gwiazdy, linia wzroku aparatu wychodząca z pozycji A przetnie się z nową linią w punkcie OA, a wychodząca z pozycji B, w punkcie OB. Kąty pomiędzy liniami wzroku aparatu i kierunkiem do gwiazdy w pozycjach A i B to odpowiednio α i β.
    

   

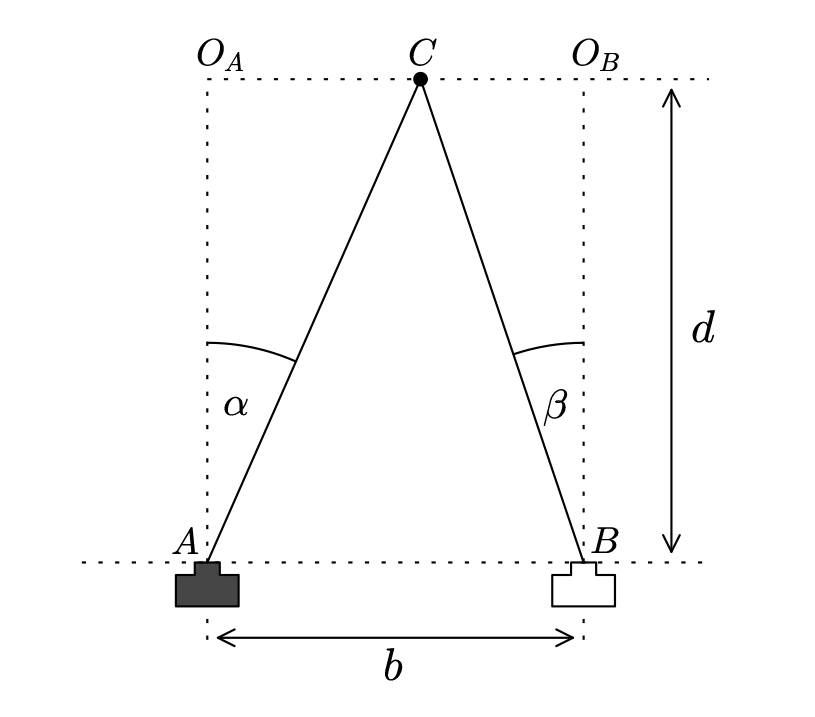
   W przeciwieństwie do teodolitów, aparaty nie umożliwiają bezpośredniego pomiaru kątów. Dlatego konieczne jest odniesienie lokalizacji gwiazdy na ekranie aparatu do kąta promieni świetlnych pochodzących z gwiazdy gdy aparat jest w różnych pozycjach.

2. W tym celu należy wyobrazić sobie nieco uproszczoną sytuację fikcyjną. Najpierw potraktujmy obiektyw aparatu jak otwór – jak pokazano to na ryc. 3, gdzie P to pozycja obiektywu. Promień światła porusza się więc w linii prostej od gwiazdy przez obiektyw aparatu i uruchamia czujnik fotograficzny na ekranie w odległości f (ogniskowa obiektu) w tylnej części aparatu.
    

   

3. Po przyjrzeniu się rycinie 2 rozważmy tę sytuację z punktu widzenia aparatu i jego ruchu z A do B – jak gdybyśmy byli obserwatorem siedzącym na aparacie. Możemy to osiągnąć poprzez rzeczywiste przesunięcie pozycji aparatu z A (i odcinka AC) na prawo o odległość b, o którą przesunięto aparat tak, aby obie pozycje aparatu były takie same.

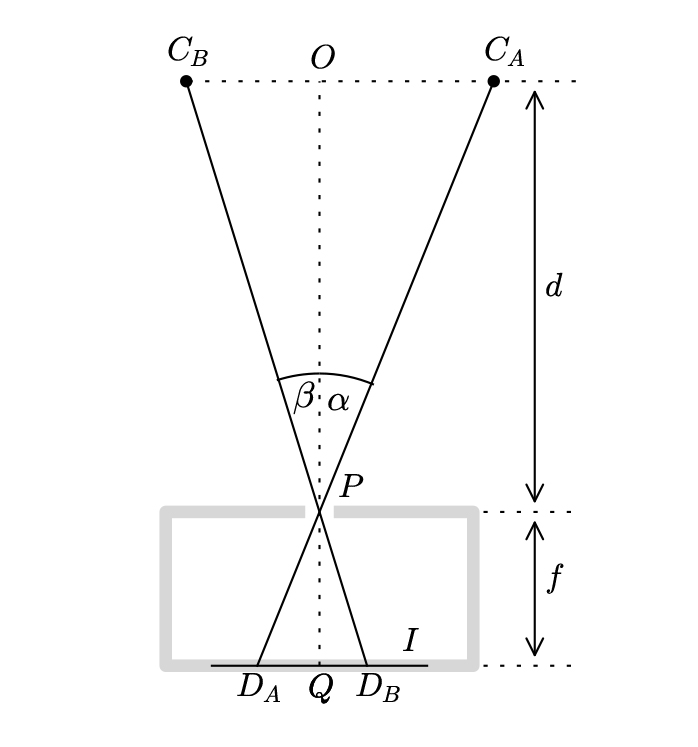
   Perspektywa aparatu pokazana jest na rycinie 3. Pozorna pozycja gwiazdy oznaczona jest jako C_A gdy aparat znajduje się w pierwszej pozycji (A), a jej obraz znajdzie się w D_A na ekranie. Analogicznie, gdy aparat zostanie ustawiony w punkcie B, pozorna pozycja gwiazdy to C_B, a jej obraz to D_B. (Tutaj odcinek OQ to odległość pomiędzy płaszczyzną obrazu aparatu a równoległą do niej płaszczyzną zawierającą gwiazdę.) Odcinek C_BC_A to odległość b z ryciny 2, a kąty a i ß pozostają takie same.
    

4. Po przyjrzeniu się tej geometrii widzimy, że niektóre trójkąty są do siebie podobne. Dostarczą nam one wzór na połącznie odcinka d z innymi znanymi odcinkami b oraz f, co pozwoli obliczyć jego wartość. Z materiałów dodatkowych dowiesz się, jak wyprowadzić ten wzrór^w1.

   Wzór to:

   
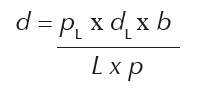
   gdzie:
   d = odległość od gwiazdy
   L = rzeczywista długość przedmiotu kalibrującego
   b = rzeczywisty odcinek, o jaki przesunięty został aparat (który odpowiada odległości od C_A do C_B)
   d_L = rzeczywista odległość przedmiotu kalibrującego do podstawy aparatu (wzdłuż odcinka OQ)
   p = odległość w postaci liczby pikseli pomiędzy obrazami gwiazdy (w D_A oraz D_B)
   p_L= długość jako liczba pikseli obrazu przedmiotu kalibrującego
    

5. Aby użyć wzoru należy najpierw skorzystać z programu do przetwarzania obrazów, aby znaleźć p, liczbę pikseli (na osi poziomej) oddzielających pozycje obrazu gwiazdy na obu zdjęciach widzianych na ekranie. Możesz również użyć programu do obliczenia p_L, długości przedmiotu kalibracyjnego przedstawionego w postaci liczby pikseli na ekranie.

Obliczenie wartości d oznacza, że udało ci się z pomocą paralaksy wyznaczyć odległość do gwiazdy.

Teraz przy pomocy taśmy mierniczej bezpośrednio zmierz odległość d i porównaj ją z obliczoną wartością paralaksy. Jak precyzyjny okazał się otrzymany wynik?

Ćwiczenie można powtórzyć z “gwiazdą” umieszczoną w różnych odległościach aby ustalić, czy precyzja pomiaru paralaksy zmienia się z odległością (zobacz poniżej część “Jakiej precyzji możemy się spodziewać?”).

Fotograficzne pomiary paralaksy z punktem odniesienia

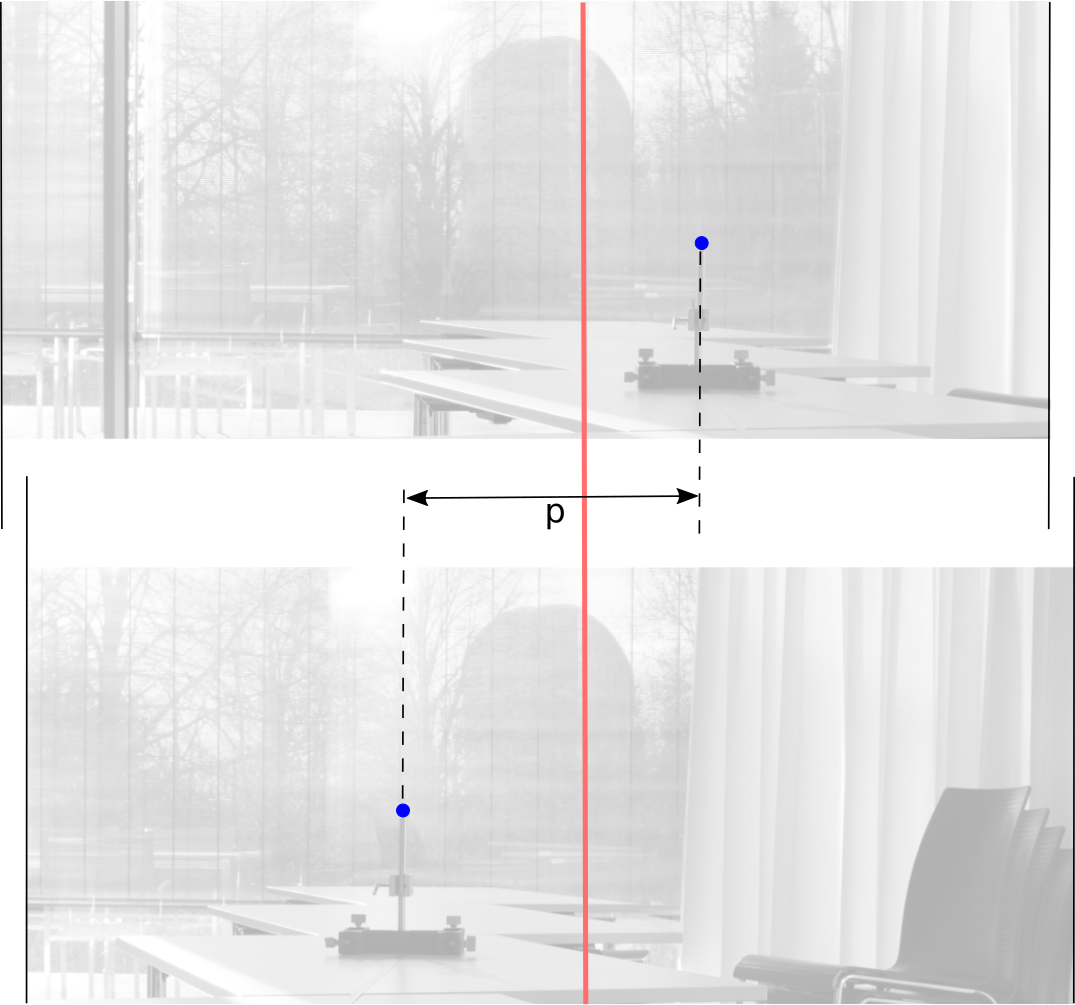
W celu uzyskania większego astronomicznego realizmu możemy dostosować metodę fotograficznego pomiaru paralaksy i użyć obiektu odniesienia poza salą lekcyjną. Obiekt powinien znajdować się zdecydowanie dalej niż „gwiazda”. W tym ćwiczeniu zamiast opierać się na aparacie wycelowanym w tym samym kierunku po przesunięciu z punktu A do B, wybieramy odległy obiekt odniesienia widoczny na obu fotografiach. Następnie mierzymy odległość gwiazdy do obiektu odniesienia na każdym zdjęciu w pikselach. To alternatywne podejście opisane poniżej, powinno dać bardziej precyzyjne rezultaty.

Procedury

1. Znajdź obiekt odniesienia, czyli drobny szczegół najdalszego z obiektów widocznych na obu fotografiach – musi być on bardziej odległy niż model gwiazdy. My na punkt odniesienia (znacznik) wybraliśmy element na jednej z kopuł obserwacyjnych Astronomicznego Instytutu Maxa Plancka, oddalonych od aparatu o jakieś 80 metrów.
    
2. Narysuj pionową linię przecinającą punkt odniesienia na każdej fotografii. To linia odniesienia. Możemy teraz użyć jej do obliczenia ilości pikseli, o jaką przesunięta została „gwiazda”, jak pokazano na rycinie 4.
    

   

3. Aby obliczyć p, czyli odległość na ekranie liczoną w pikselach, należy na początku odnaleźć odległość w pikselach modelu gwiazdy od linii odniesienia na każdym ze zdjęć z osobna. Następnie należy dodać do siebie te poziome wartości (bezwzględne) w pikselach, aby wyznaczyć p. Na przykład, -24 px to 24 piksele na lewo od linii odniesienia, a +36 px to 36 pikseli na prawo, co daje odległość p równą 60 pikselom.
    
4. Od tego momentu obliczenia będą takie same jak przy poprzedniej metodzie (zobacz sekcję powyżej, „Pomiar odległości do gwiazdy”).

Jakiej precyzji możemy się spodziewać?

Jak precyzyjne będą zatem wartości otrzymane przy pomocy udoskonalonej metody? Nasze dane wykazują, że mogą być one niezwykle precyzyjne (w porównaniu z rzeczywistym pomiarem odległości), jak pokazano na rycinie 5. Największy błąd procentowy to zaledwie 3,2%. 

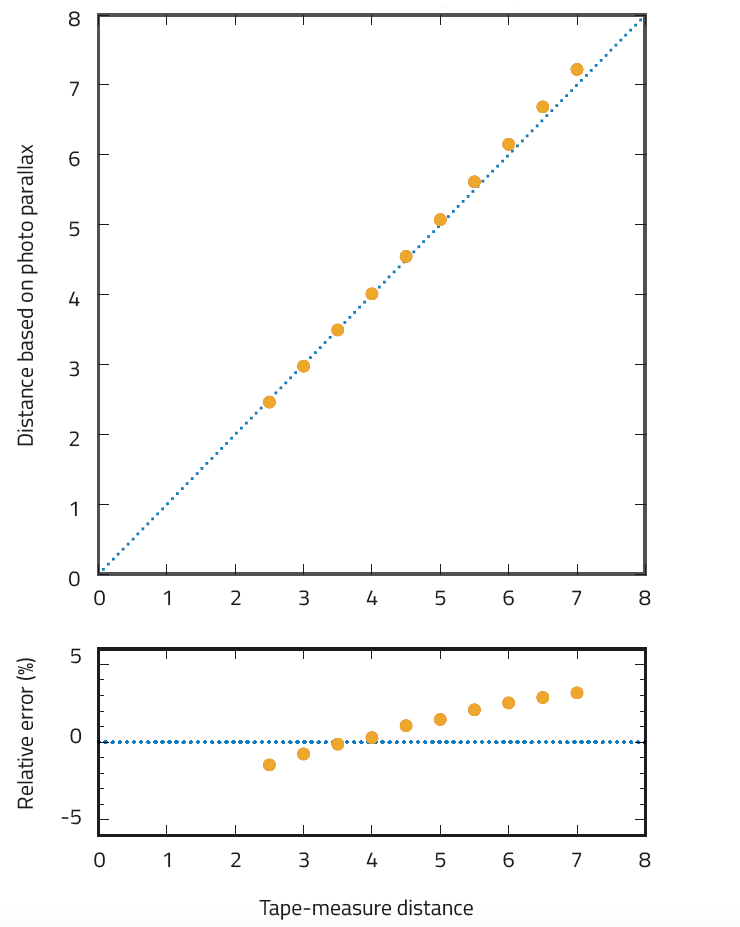
Zwróć uwagę, że w przypadku dużych odległości błąd procentowy oraz rzeczywisty są większe. Wynika to ze zmiany w geometrii: odległość do modelu gwiazdy rośnie w porównaniu do odległości do obiektu odniesienia, więc błąd wprowadzony przez paralaksę obiektu odniesienia jest jeszcze większy.

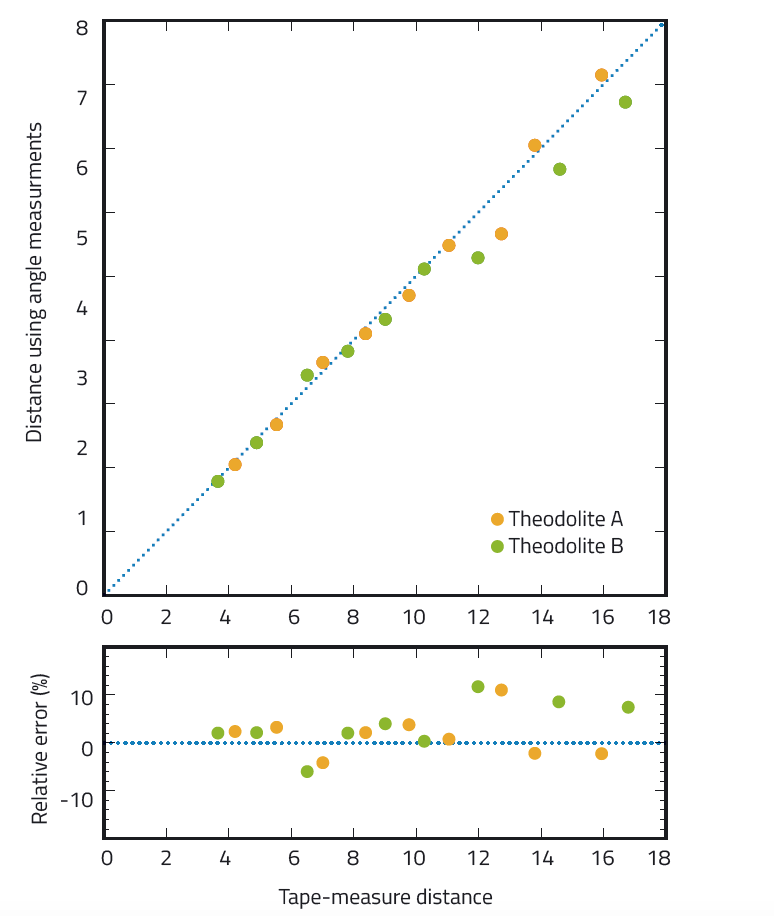
W przypadku prostej metody pomiaru kątów opisanej w poprzednim artykule (Pössel, 2017), precyzja pomiarów odległości była znacznie mniejsza – ogólnie rzecz biorąc wynosiła około 10%, jak pokazano na rycinie 6. Metoda opisana w niniejszym artykule jest zatem znacznie udoskonalona w zakresie precyzji w porównaniu z metodą poprzednią, gdzie głównym źródłem błędu były pomiary kątowe.