La geometria ti può portare sulla Luna Teach article
Tradotto da Rocco G. Maltese. Misura della distanza tra la Terra e la Luna utilizzando la geometria che si studia nella scuola superiore e una rete internazionale di scuole e di osservatori.

spazio.
Immagine gentilmente
concessa dalla NASA
Immaginate di allungare un braccio e guardare il vostro pollice, prima con un occhio e poi con l’altro. L’apparente spostamento del pollice rispetto allo sfondo è chiamato parallasse. Lo stesso principio si può applicare a due scuole se ‘osservano’ la Luna dalle due posizioni differenti in cui si trovano: esse la vedranno leggermente spostata rispetto alle stelle fisse dello sfondo.
In questa attività, diverse scuole, site in differenti continenti si coordinano così che studenti dell’età dai 16 – 19 anni, in contemporanea potranno confrontare le loro osservazioni della Luna effettuate da luoghi diversi e calcoleranno la sua distanza dalla Terra (figura 1). Avendo a disposizione una macchina fotografica e una buona conoscenza della geometria, l’esperienza dura 2 ore circa per l’osservazione e 3 ore per i calcoli (trovare un partner potrebbe richiedere un tempo leggermente più lungo…..).
DDefinizione delle condizioni ottimali
Lo schema generale delle osservazioni per questa attività è riportato dettagliatamente in figura 1, dove M è la Luna, rappresentata da un punto date le sue dimensioni molto piccole rispetto alla distanza calcolata (approssimativamente 1/100mo)
Come in molte imprese scientifiche, la pianificazione è fondamentale. In questo caso, oltre a definire le condizioni ottimali per effettuare l’osservazione, l’insegnante ha la necessità di determinare quale margine d’errore può essere accettabile: questo è importante in modo che gli alunni non restino delusi se non troveranno la distanza precisa. Qui di seguito abbiamo elencato un certo numero di punti da mettere in risalto al momento della discussione dell’attività in classe, ma anche quando si pianificherà la collaborazione con un altra scuola.
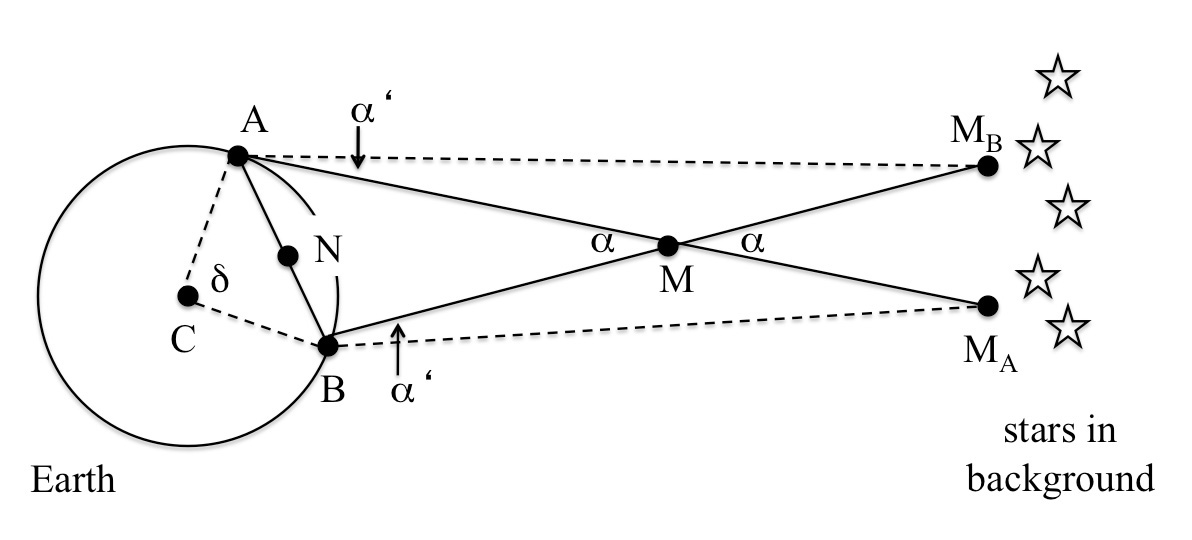
Immagine gentilmente concessa dagli autori
La Figura 1 mostra come due osservatori (A e B) vedranno la Luna, M, come se si trovasse in due posizioni in cielo leggermente spostate l’una rispetto all’altra. Anche se in realtà i due punti di osservazione, A e B, la Luna M, e il centro della Terra, C, non giacciono sullo stesso piano, supponiamo che ciò avvenga, in modo da semplificare i calcoli e utilizzare unicamente la trigonometria piana.
corpo celeste.
Immagine gentilmente
concessa da Nicola Graf
Affinché l’approssimazione sia la più esatta possibile, i due punti di osservazione devono trovarsi alla stessa longitudine, e la Luna si dovrebbe trovare al momento dell’osservazione, alla sua più alta posizione in cielo (culminazione)w1. Questa situazione, piuttosto ideale è molto difficile da ottenere ma raccomandiamo che ci si avvicini il più possibile, e che, allo stesso tempo si sia consapevoli dell’errore che si commetterebbe allontanandosi significativamente da queste condizioni.
Inoltre se l’angolo che forma la Luna con l’equatore celeste (declinazione)w1 fosse uguale alla media tra le latitudini di A e B, ABM formerebbe un triangolo isoscele e questo semplificherebbe ulteriormente i calcoli.
Procurarsi uno sfondo appropriato in cielo
È necessario poter osservare, sulla volta celeste, almeno due stelle brillantiw1(o pianeti) di sfondo per determinare le due posizioni apparenti della Luna, MA e MB.
Assunzioni geometriche
Osserviamo che le due rette AMA e BMA sono quasi parallele, come lo sono AMB e BMB. Questo significa che vale la relazione α ≈ α’ (figura 1). Anche se questa assunzione non è strettamente vera, è accettabile considerando il fatto che la coppia di rette convergono in un punto molto distante sia dalla Terra che dalla Luna. Naturalmente, questo nella figura 1 non appare non essendo tale figura in scala.
Se misuriamo l’angolo α e la distanza AB – detta base della parallasse – più un altro angolo nel triangolo ABM, possiamo calcolare tutte le altre distanze. In alternativa, possiamo rendere il triangolo ABM isoscele, e conoscere α e AB è sufficiente per determinare tutte le altre distanze.
Un punto chiave è che la base della parallasse sia abbastanza lunga, rispetto alla distanza che vogliamo determinare, per evitare che l’angolo di parallasse diventi troppo piccolo. Per la Luna, una distanza tra le scuole partner di circa 1000 km dovrebbe essere sufficiente, tenendo conto però che più distante sono le scuole e meglio sarà.
Ci potrebbero essere ancora degli errori…
Nonostante la cura posta nello scegliere la migliore condizione possibile, le misure potrebbero non essere ancora perfette. Le principali fonti d’errore possono essere:
- Imprecisione nel determinare la differenza di posizione della Luna nelle due immagini, principalmente a causa della sovraesposizione del disco Lunare;
- A, B, C ed M potrebbero non giacere esattamente sullo stesso piano;
- Distorsione dovuta alle lenti della macchina fotografica;
- Condizioni del cielo non ottimali;
- Rifrazione atmosferica;
- Sincronizzazione dei tempi.
Gli errori dovuti alle cause d) ed e) non sono molto importanti: l’osservazione si basa sulla misura di grandi angoli per cui una piccola imprecisione di alcuni secondi d’arco non dovrebbe influenzare il risultato.
La sincronizzazione nei tempi (f) analogamente non è molto importante, sia perché la Luna viaggia percorrendo una distanza pari al suo diametro, in un’ora, così che una sincronizzazione imprecisa di alcuni secondi (o addirittura di minuti) non è così rilevante.
La distorsione dovuta alle lenti della fotocamera (c) può essere ridotta utilizzando un teleobiettivo. Un obiettivo normale produce un errore maggiore, ma ancora accettabile. Nel nostro caso, l’angolo non era così piccolo e abbiamo stimato che si è prodotta una imprecisione approssimativamente dell’1-2%.
Gli errori dovuti alle cause a) e b) sono i più importanti, e possono dar origine ad una imprecisione del 5-10% ciascuno. Insieme, possono quindi generare un’errore del 10-20%. Per ridurre a) dobbiamo scegliere una base della parallasse più lunga così che lo spostamento della Luna nelle due immagini sia il più grande possibile; per ridurre b) dobbiamo scegliere opportunamente luoghi e momenti per le osservazioni così che A, B, C ed M si vengano a trovare sullo stesso piano. Se entrambe queste condizioni saranno rispettate (per noi, la prima condizione è stata rispettata ma non la seconda), l’errore si riduce a qualche percento.
Il network osservativo
Abbiamo creato una rete di scuole, osservatori ed insegnanti su tutto il pianeta per intraprendere queste misure. Questa rete era formata dai seguenti membri:
- Mario Koch, insegnante presso il Friedrich-Schiller-Gymnasyum in Weimar, Germania
- Noorali Jiwaji, lettore di fisica presso la Open University della Tanzania a Dar es Salaam, Tanzania
- Frank Oßwald, insegnante presso Goethegymnasium in Weissenfels, Germania
- Matthias Penselin, insegnante alla Albert Schweitzer Gymnasium Crailsheim e alla House of Astronomy in Heidelberg, Germania
- Alexander GM Pietrow, Iosto Fodde e Jelle Mes, studenti dell’Osservatorio di Leiden e membri del comitato osservativo del Leidsch Astronomisch Dispuut ‘F. Kaiser’, Leiden, Netherlands (Olanda)
- Elena Servida, insegnante presso il Liceo Vittorio Veneto in Milano, Italia
- Brian Sheen, del l’ Roseland Observatory, St Austell, UK
Attraverso questa rete, autonomamente, gli insegnanti hanno potuto proporre date ed effettuare osservazioni per calcolare la distanza tra Terra e Luna.
La grande distanze tra le scuole della nostra rete garantisce una base sufficientemente grande (distanza AB) da rendere possibile anche la misura della distanza di Marte dalla Terra nel Maggio 2016 (Cenadelli, et al. 2009; Penselin et al., 2014). In questa data, la Terra si troverà tra il Sole e Marte, Marte a sua volta si troverà alla distanza minima dalla Terra, nella posizione ideale per questo tipo di osservazioni.
Se voleste contattare uno qualsiasi dei partecipanti a questa rete internazionale per realizzare delle misurazioni, potete contattare Davide Cenadelli attraverso la sua email davide.cenadelli@unimi.it
Materiale
L’unico strumento necessario è una fotocamera di qualità che permetta di scattare delle foto della Luna e del cielo. Un teleobiettivo con una lunghezza focale di circa 100-200 mm è l’ideale, ma obiettivi normali funzioneranno altrettanto bene se le stelle brillanti o i pianeti sullo sfondo non saranno troppo vicine alla Luna.
Procedura
- Utilizzare il network osservativo (vedi box) per trovare una scuola o osservatorio che abbia la stessa longitudine della propria scuola.
- Prendere nota della latitudine e della longitudine dei due partners (λ = latitudine , l = longitudine). Nel nostro caso abbiamo utilizzato le osservazioni realizzate a Cape Town, Sud Africa, e all’Osservatorio Astronomico della Regione Autonoma della Valle D’Aosta (OAVdA), Italia:
OAVdA, Italy: (λI 45.78° N, lI 7.48° E)
Cape Town, Sud Africa: (λS 33.93° S, lS 18.42° E) - Concordare la data e l’ora esatta per l’osservazione della Luna (potrebbe essere meglio concordare più momenti nel caso di avverse condizioni meteo). Nel nostro caso abbiamo concordato di effettuare un’osservazione simultanea il 2 Febbraio 2015 alle 20.02 UT. Quella mattina si vedevano in cielo due corpi celesti di riferimento
,molto luminosi, Giove e Procione (α CMi), non distanti dalla Luna, che sono serviti da punti di riferimento per misurare lo spostamento della Luna.
Le migliori circostanze si verificano quando sono presenti sulla volta celeste pianeti o stelle molto brillanti, come Giove e Procione nel nostro caso, visibili in prossimità della Luna, ed anche il più vicini possibile essendo piccolo il campo visivo del teleobiettivo. Il teleobiettivo aiuta ad evitare gli effetti di distorsione tipici delle lenti grandangolari. - Per le date scelte, tutti i partecipanti che hanno un cielo sereno dovrebbero effettuare, diverse riprese della Luna, seguendo la tabella dei tempi predeterminata. Le immagini dovrebbero mostrare il più chiaramente possibile la Luna e i due astri brillanti di riferimento. E’ utile riprendere le immagini con differenti tempi di esposizione, per poter scegliere il miglior compromesso tra una immagine con la Luna non eccessivamente sovraesposta e le stelle di sfondo comunque visibili.
- Sovrapporre le immagini di due differenti osservatori e farla diventare una singola immagine, come mostrato in figura 2.

Immagine gentilmente concessa dagli autori
- Misurare la distanza fra Giove e Procione su una delle immagini, e riscalare l’altra per far coincidere tale distanza ottenendo così la stessa scala;
- Sovrapporre le immagini e prendere nota della posizione della Luna come osservata da entrambe le scuole sulla stessa immagine;
- Misurare la differenza delle posizioni del centro della Luna.
- Calcolare la base delle parallasse, AB, come mostrato in figura 1.
L’angolo, δ, tra i due osservatori A e B può essere calcolato come segue (Roy & Clarcke 1977):
cos δ = sin λI sin λS + cos λI cos λS cos(lI − lS )
= −sin (45.78°) sin (33.93°) + cos (45.78°) cos (33.93°) cos (10.94°)
= 0.1681
δ = 80.32° (1)
Ipotizzando la Terra perfettamente sferica di raggio 6367 km, la base AB è data da:
AB = 2BN
= 2(CB * sin (δ/2))
= 2 × 6367 km × sin (80.32°/2)
= 8212 km (2) - Calcolare la parallasse, α.
Utilizzando semplicemente un righello, possiamo stimare quale sia la differenza nella posizione della Luna (figura 2) che risulta essere 2,4 diametri lunari. Il diametro della Luna, visto da Terra, sottende un angolo di 0,5°; cioè, se tracciamo due rette uscenti dall’occhio dell’osservatore sino agli estremi del diametro lunare, l’angolo tra queste due rette è di 0.5°.
Perciò, se un diametro lunare corrisponde a 0.5°e l’apparente spostamento della Luna osservato è di 2.4 diametri lunari, allora:
α = 2.4 * 0.5 = 1.2° - Calcolare la distanza tra la Luna e il centro della Terra, CM.
Calcoleremo CM in due casi. In entrambi i casi assumiamo che A, B, M e C giacciano sullo stesso piano.
Caso 1: ABM è un triangolo isoscele
In questo caso, gli angolo BAM e ABM sono uguali, e:
CM = CN+NM
= CA cos δ/2 + ([AB/2]/[tan α/2])
= 4866 + 392 080 km
= 396 900 km (3)
La distanza nota all’istante delle osservazioniw1 era di 397 900 km, per cui abbiamo ottenuto un valore sottostimato dello 0.3% soltanto. A causa delle approssimazioni introdotte, la precisione ottenuta è da attribuirsi in parte alla fortuna.
Caso 2: ABM non è un triangolo isoscele
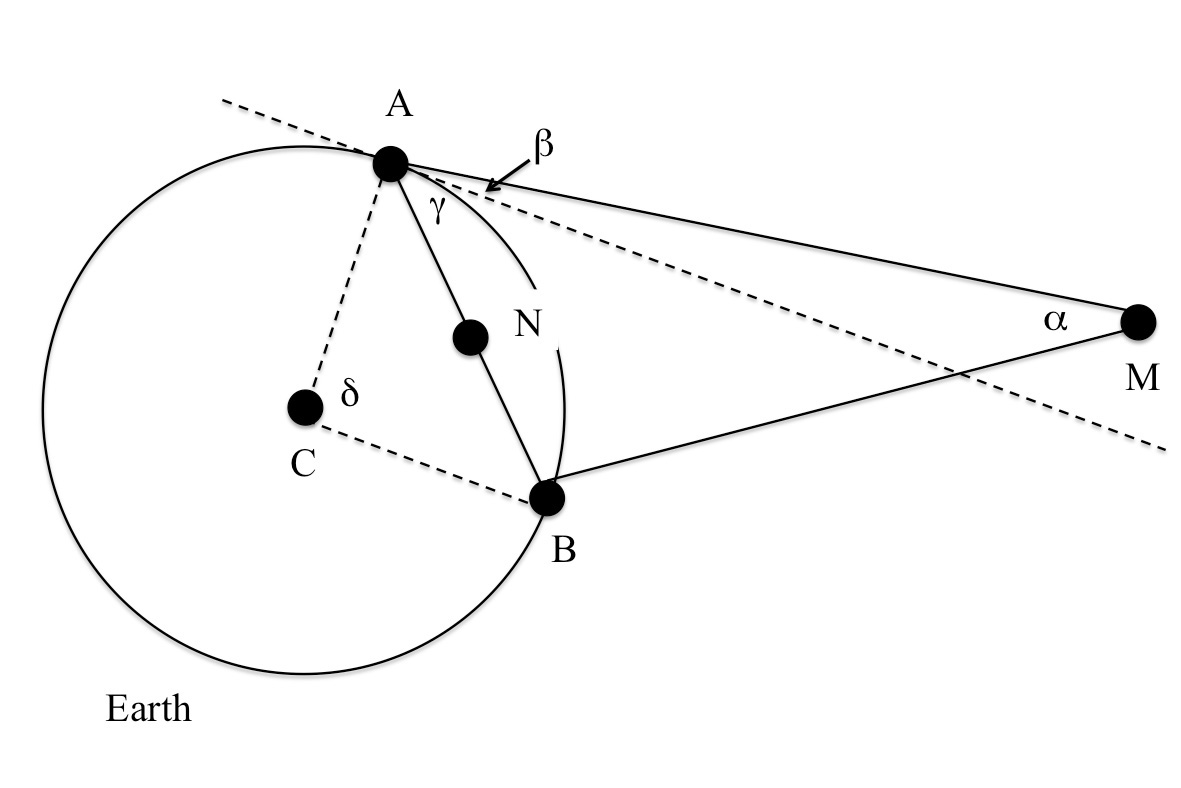
Figura 3: Ingrandimento della sezione di figura 1 che mostra la distanza tra la Terra e la Luna, e gli angoli β e γ.
Immagine gentilmente concessa dagli autoriSe lasciamo cadere l’ipotesi che ABM sia un triangolo isoscele, abbiamo bisogno di conoscere il valore di un altro angolo, come BAM. BAM è uguale alla somma di β, cioè l’altezza della Luna sull’orizzonte di A, e γ (vedi figura3). β può misurato con uno strumento adeguato, o se è indisponibile, può essere assunto uguale all’altezzaw1 di una delle stelle o pianeti di riferimento utilizzati per misurare la differenza della posizione della Luna. Per Procione abbiamo usato β = 39.3°.
Possiamo calcolare γ utilizzando il valore per δ calcolato precedentemente utilizzando la regola geometrica secondo cui: γ = δ/2.
Ne segue che BAM = β + γ = 79.5°.
Finalmente, se applichiamo la legge dei seni al triangolo ANM, avremo:
ΝM/sin79.5° = AN/sin(α/2)
ΝM = AN (sin79.5°/sin0.6°)
≈ 385 536 km (4)
e quindi:
CM = CN + NM
= CAcosα/2 + NM
= 4866 + 385 536 km = 390 400 km (5)
Questo risultato è ancora realistico ed è solamente 1.9% minore del valore conosciuto.
Ringraziamenti
Gli autori desiderano ringraziare caldamente tutti i partecipanti alla nostra rete, e anche gli studenti che hanno partecipato all’ESO Camp 2014 e che hanno realizzato una misura di questo tipo.
L’Osservatorio Astronomico della Regione Autonoma della Valle d’Aosta è finanziato dalla Regione Autonoma Valle d’Aosta, il Comune di Nus e la Unité des Communes valdôtaines Mont-Émilius. Andrea Bernagozzi ha condotto parte del lavoro per questo progetto con un finanziamento del Fondo Sociale Europeo dell’Unione Europea, la Regione Autonoma Valle d’Aosta e il Ministro del Lavoro e delle Politiche Sociali.
References
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11: 72-77
- Roy AE, Clarcke D (1977) Astronomy: Principles and Practice. Bristol, UK: Adam Hilger. ISBN: 0852743467
Web References
- w1 – Per trovare i valori necessari ai calcoli descritti nell’articolo, si può utilizzare Stellarium, un simulatore astronomico open – source (gratuito) installabile con qualsiasi sistema operativo (N.d.T.).
Resources
- Il metodo utilizzato in questo articoli è descritto anche in molti libri di testo di astronomia. Per esempio, vedi:
- Karttunen H et al (2007) Fundamental Astronomy 5th edition. Berlin, Germany: Springer. ISBN: 9783540341437
- Con riferimento al materiale didattico di Penselin et al. (2014), utilizzabili direttamente in classe, si possono trovare nel sito web Wissenschaft in die Schule (solo in Tedesco).
Review
Questo articolo descrive in un modo simpatico come riunire alcuni argomenti tipici della matematica con argomenti di altre scienze, come la fisica. Mostra come calcolare la distanza la distanza della Luna ed eventualmente di Marte utilizzando i soli dati provenienti dalle immagini di una fotocamera prese in collaborazione con istituzioni partner (ad esempio attraverso il network osservativo). Utilizzando matematica pura – o matematica applicata pura, potrete risolvere un problema reale – ottenendo dei buoni risultati.
A causa della sua breve ma efficace introduzione, questo articolo può essere utilizzato sia dagli insegnanti di scienze che dagli insegnanti di matematica.
Gerd Vogt, (Scuola Secondaria Superiore per l’Ambiente e l’Economia) Higher Secondary School for Environment and Economics, Yspertal, Austria





