Saving the Earth Hollywood-style Teach article
Challenge your students to save the Earth from an asteroid collision, using calculations based on the Hollywood sci-fi fantasy film Armageddon.
What would students prefer to discuss: Hollywood films or physics? In my physics classes, I try to combine these topics by using scenarios from Hollywood sci-fi films as a source of problem-solving exercises – in a similar way to using the adventures of superhero characters (see Follows, 2017). Even if students have not seen the films, they seem to enjoy engaging with the inventive and fantastical scenarios, which they can use as a basis for doing real science – as long as the ideas and assumptions are set out clearly.

geralt/pixabay.com
In this article, I present some exercises based on the film ‘Armageddon’ (1998) – a Hollywood movie about a heroic mission to save the Earth from a giant asteroid heading straight towards it. The film was criticised for being rather unrealistic, but it still offers an interesting plot to use as a basis for calculations.
Armageddon: the story
In the film, astronomers spot an asteroid the size of Texas heading towards Earth when it is only 18 days away from impact. A plan is devised to detonate a nuclear warhead beneath the surface of the asteroid, to split it into two equal halves along a fault line. The two halves would then move apart – and miss the Earth. To execute the plan, NASA flies oil-driller Harry Stamper (Bruce Willis) and his team to the asteroid on board two space shuttles, which perform a slingshot around the Moon and come up behind the asteroid. Once they reach the asteroid, to avert disaster they must detonate the bomb before the asteroid reaches ‘zero barrier’, a point reached eight hours after the asteroid passes the Moon.
Creating a classroom activity
Students can carry out a variety of calculations based on the information in the film, supplemented by some reasonable assumptions. The fun lies in seeing whether the quantities and assumptions in the film make sense – or not.
From the film, we know that:
- The asteroid is ‘the size of Texas’. Let’s assume that this refers to the cross-sectional area through the centre of the approximately spherical asteroid.
- The asteroid is heading towards Earth at a speed of 22 000 miles per hour.
- Each half of the asteroid misses the Earth’s surface by 400 miles (640 km).
The other information we need is as follows:
- Texas has an area of 696 200 km2.
- The average density of the four largest known asteroids is 2760 kg m-3. (For comparison, the Earth has a density of 5520 kg m-3.)
- The distance of the Moon from Earth is 384 400 km.
- Earth has a radius of 6400 km.
- The energy of a nuclear warhead is up to 50 megatons of TNT. (This is the energy of the most powerful thermonuclear weapon known: the Soviet warhead called Big Ivan.)
- 1 megaton of TNT is 4.18 x 1015 J
Let’s also assume that:
- The asteroid is heading for the centre of the Earth, so that both halves of the asteroid need to move ‘sideways’ by the same distance.
Student questions and worked calculations
Students are asked to investigate whether the plan is likely to succeed in saving Earth from the collision. This can be done as a sequence of calculations, set out below. Students work in groups, and are encouraged to discuss the way forward with each other.
1. Show that the asteroid has a radius of 470.8 km.
We assume that the approximately circular cross-section of the asteroid has an area A equal to that of Texas, i.e. approximately 696 200 km2.
A = πr2 where r = radius of asteroid.
So:

2. At what speed is the asteroid travelling in metric units (i.e. in m s-1)?
Encourage the students to perform the change of units formally:

3. How far from Earth is ‘zero barrier’?
To answer this question, we first need to work out how far the asteroid would travel in eight hours, as the ‘zero barrier’ is a distance equal to eight hours travel from the Moon:
Distance = speed x time
= 9833 m s-1 x 8 x 3600 s
= 2.83 x 108 m
Then, we subtract this distance from the overall Earth–Moon distance (3.84 x 108 m) to calculate how much further the asteroid would need to travel to collide with the Earth.
3.84 x 108 m – 2.83 x 108 m
= 1.01 x 108 m
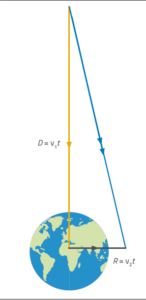
yellow line shows the
asteroid’s original direction
of travel. The black line
shows how far one half of
the asteroid has to move to
miss the Earth by 640 km;
the blue line shows the
resultant path that the half-
asteroid needs to take.
Mike Follows/Nicola Graf
4. How fast do the two pieces of the asteroid need to move apart to avoid impact with Earth?
The two halves of the asteroid must travel 1.01 x 108 m from the zero barrier to reach Earth. In the time this takes, each half-asteroid must also move in a direction perpendicular to the original direction of travel, far enough to miss the Earth by at least 640 km on each side (see figure 1).
Here:
D = distance between zero barrier and Earth
R = radius of the Earth plus the 640 km by which each half misses the Earth
v1 = speed of the asteroid moving towards Earth
v2 = perpendicular (sideways) speed of each half-asteroid needed to miss the Earth with a margin of 640 km
The speed v2 can be calculated in two ways.
Method 1
First, we calculate how long it would take (time t) for the asteroid to travel from the zero barrier to Earth:
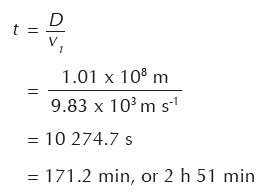
We can now work out the speed that each half of the asteroid needs to move in a direction perpendicular to its original path to miss the Earth with a margin of 640 km.
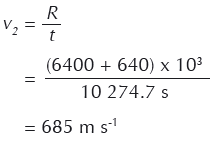
Method 2
For those students who are more confident with maths, we can use proportionality. As in the method above, in the time t that it takes the asteroid to travel 101 000 km to Earth, the two pieces must move apart by a distance equivalent to the radius of the Earth plus 640 km, R. So using algebra:

5. What is the mass of the asteroid (assuming it has a density typical of asteroids)?
The mass m is equal to density ρ times volume V, so m = ρ x V
The asteroid is approximately spherical, so V = 4 ⁄ 3 π R3
From question 1, R = 470.8 km
So M = ρπR3
= 2760 kg m-3 x 4/3 π x (4.71 x 105 m)3
= 1.21 x 1021 kg
6. How much kinetic energy must be given to the two halves of the asteroid to prevent a collision with Earth?
Note: you will get the same answer whether the asteroid is treated as one lump or two separate pieces.
E = 1/2 mv2
= 1/2 x 1.2 x 1021 kg x (685 m s-1)2
= 2.84 x 1026 J
7. How many nuclear weapons of the same size as Big Ivan would be needed to provide this energy?
One Big Ivan is equivalent to 50 megatons of TNT
= 50 x 4.18 x 1015 J
= 2.09 x 1017 J
So the energy required to change the path of the asteroid sufficiently to miss the Earth is equivalent to:
![]()
8. How fast will the two halves of the asteroid move apart if only one Big Ivan bomb is used?
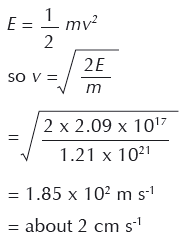
9. How far apart will the two halves be when they collide with Earth, if only one Big Ivan bomb is used?
We have already shown (in question 4) that at the zero barrier, the asteroid is less than three hours away from impact. At a speed of 1.85 x 102 m s-1 (question 8), in that time each half of the asteroid will have moved 190 m away from its original path, so that the two halves will have moved apart by less than 400 m – far too little to avoid a collision with Earth. In fact, under the circumstances described in the film, the team would need to intercept the asteroid when it was some 3.74 x 1012 km away – 25 times the distance of the Sun from Earth, out in space between Uranus and Neptune.
Which all goes to show that there are times when you need something even bigger than a nuclear explosion to make things happen.

Jack W. Aeby (public domain)/Wikimedia Commons
Discussion
There is plenty more here to discuss with students, after or alongside the calculations. Students may well have their own thoughts on how to make the scenario more realistic – and on which outcomes or assumptions are the most absurd. For example, why did the scientists fail to spot the asteroid until it was so close? And despite this failure, how did they work out that it had a fault line running through it, exactly along the direction of travel?
Here are some suggestions of other points to consider:
- The calculations did not include the energy required to break the chemical bonds to split the asteroid in two: it included only the energy required to move the two halves apart, assuming that the asteroid was already conveniently fractured. If we added the energy needed to fracture the asteroid, by how much would this affect the calculations?
- If the asteroid were to hit the Earth, what would be the energy of the impact? Students can work this out from the kinetic energy of the asteroid. They will find that its impact with the Earth would release 5.8 x 1028 J – equivalent to 276 billion (2.76 x 1011) Big Ivans. For comparison, the asteroid that marked the end of the Cretaceous (and the demise of the dinosaurs) 65 million years ago is estimated to have released only about 4 x 1023 J (2 million Big Ivans).
- Students can investigate real-life objects that might strike the Earth, and find out how typical the asteroid in Armageddon is for asteroids generally. At 9833 m s-1, its speed is somewhat slower than asteroids on average, which have a mean velocity of 25 000 m s-1. (For comparison, Halley’s comet has a velocity of 53 600 m s-1 when it is closest to the Sun, at perihelion.) NASA’s NEOw1 (near-Earth object) programme searches for and tracks objects that might strike the Earth: one candidate is asteroid (29075) 1950 DA, which has a diameter of about 1 km. Its chances of hitting the Earth in 2880 is currently estimated to be 1 in 300.

References
- Follows M (2017) Heroes and villains: the science of superheroes. Science in School 40: 57-63.
Web References
- w1 – To read the latest news stories from the Center for Near Earth Object Studies, visit the NASA website.
Resources
- Read about the ‘good’ and ‘bad’ science in Armageddon by visiting the Bad Astronomy website.
- For information on asteroids and comets, visit Bill Arnett’s very comprehensive Nine Planets website.
- Watch a TED talk explaining how we could defend the Earth from asteroids on the TED website.
- The Spaceguard Centre (located in Knighton, Powys, UK) provides information about the threat of asteroid and comet impacts, and the ways in which we can predict and deal with them. For more information, visit their website.
- The Views of the Solar System website offers a catalogue of terrestrial impact craters.
- For other critiques and explorations of science in the movies, see the following books:
- Rogers T (2007) Insultingly Stupid Movie Physics. Naperville, IL, USA: Sourcebooks Hysteria. ISBN: 1402210337
- Perkowitz S (2010) Hollywood Science: Movies, Science, and the End of the World. New York, USA: Columbia University Press. ISBN: 0231142811
- Weiner A (2007) Don’t Try This at Home! The Physics of Hollywood Movies. New York, USA: Kaplan Publishing. ISBN: 1419594060
- Edwards R, Brooks M (2017) Science(ish): The Peculiar Science Behind the Movies. London, UK: Atlantic Books. ISBN: 1786492210
Review
This activity is very interesting and fun for students. What better way to trigger students’ curiosity and to prompt them to think creatively? Verifying or disproving facts derived from fictional films allows students to generate their own questions about them, and to think of how these questions can be answered by applying their knowledge of physics and mathematics. No matter how surreal some scenes in these films are, there will always be a scientific principle that can help explain their possibility or impossibility.
The use of science to explain fictional movies can also lead to some very elaborate discussions when students think about the facts stated in films and do not just take them for granted. Students can be motivated to expand their area of research as needed, and to back up their arguments with mathematical evidence. This exercise can also make students aware that science facts are everywhere, in real life as well as in fiction.
Catherine Cutajar, physics lecturer, St Martin’s College, Malta





