Physics with everyday objects: springy sweets, a universe in your pocket, and drawing circuits Teach article

Author(s): James de Winter

Sweet success: everyday objects can be used to demonstrate fundamental physical principles in an engaging manner.

Introduction

Practical and experimental work is a fundamental aspect of physics teaching and learning, but the complexity of practical activities can divert attention from the relationship that we wish students to focus on. Furthermore, students may get the idea that the principles explored apply only to that specialized experimental setup, rather than being a fundamental part of the world around them. Simple and easily accessible objects and equipment can be used to make physical principles more real to students. Here, some activities with relatively simple and easily accessible equipment that still generate quantitative data are presented. These examples also have the advantage that it may be possible for students to carry them out individually or in smaller groups than usual. In some cases, the data that students generate could be classified as somewhat ‘rough’, but it should be robust enough to demonstrate the key relationships and principles.

Activity 1: Under pressure – Hooke’s law and marshmallows

It is common to use a helical spring to show the relationship between tensile force and extension and explore Hooke’s law. In this experiment and the accompanying extension activity, this data is collected from sweet treats. Although the data from these two experiments may not be as perfectly linear as that with a helical spring, this activity helps to show that these key principles and methods apply not just to springs but to many other materials too, and this is actually the basis for standard material-testing procedures. The marshmallow experiment shows that the principles and methods apply to compression as well as tension, which is often overlooked.

Estimated time: 30 min, including graph drawing
Target age: 11–14, 14–16

Materials

  • Marshmallow (short, roughly cylindrical)
  • Two plastic drinks cups
  • Masses
  • Ruler

Procedure

  1. Place one marshmallow inside a plastic cup and then place the second cup inside the first, on top the marshmallow, squashing it between the two cups.
  2. Find the initial height of the marshmallow by measuring the distance between the rims of the two cups.
  3. Add masses inside the second cup and then measure the new distance between the rims of the cups. You can collect a set of data for mass and height of marshmallow.
A marshmallow and a stack of metal weights inside two plastic cups, next to a ruler.
Image courtesy of James de Winter
  1. By converting the mass to force (use 100 g = 1 N to make conversion easy), students can generate a set of force and height data. From this, a graph of force against reduction in height can be plotted, a best-fit line drawn, and the relationship explored. Students can examine to what extent the compressive force is proportional to the reduction in height. 

Discussion

There are opportunities here to talk about materials testing and engineering applications. Alternative versions of this experiment use cushion foam or even a kitchen measuring jug on a piece of card on top of a domestic sponge. The sponge version has the advantage that it does not need specific masses, as the volume of water in a measuring jug can be used to calculate the weight (100 ml = 100 g = 1 N).

For older students, depending on the quality of the data, stress/strain data can also be calculated, from which the value of the Young’s modulus can be calculated.

Activity 2: Elastic bands and expanding space

Estimated time: 30 min, including graph drawing
Target age: 14–16

When teaching students that the universe is expanding, understandably, it can be difficult to provide much practical work, but this activity can model some behaviours of the expanding universe. Students can collect data from the model to show that, if space is expanding, further away galaxies will be moving away faster, and this will be observed from whatever point your data is measured. It is important to emphasise that, whilst this is a model, it is useful in helping us understand the behaviour of the universe. I first found about this activity from the Perimeter Institute, and it is explained in more detail in their pack entitled The Expanding Universe.[1]

Materials

  • Four (or more) metal washers
  • Elastic/rubber bands of the same thickness
  • Metre rule
  • Tape (to fix ends of the elastic bands down when extended)

Procedure

  1. Take a set of at least four metal washers and fix them together with elastic bands in a line. The bands can be different lengths (perhaps by looping several together) but should be of the same thickness/elasticity. In this model, the washers represent galaxies; the elastic bands represent expanding space; and the whole line is the universe, or at least part of it.
  2. Students lay the washers and elastic bands out in a straight line, pick a ‘home’ galaxy, and measure the distances to each of the other galaxies, recording this data.
  3. They then stretch the whole chain and repeat the measurements. This new, stretched universe represents the original universe at some point in the future where all space has expanded.
Image courtesy of James de Winter
  1. This can be repeated with different amounts of stretch and a table of distances can be collated. A graph of increase in distance (y axis) against original distance (x axis) is plotted. Students should find that they get a straight-line graph through the origin.
  2. Students can repeat the experiment using a different home galaxy to find that the data shows the same pattern and with the same gradient. This finding can be used to help illustrate the idea that the ‘centre of the universe’ has no meaning from a cosmological perspective.

Safety note

When stretched, if the elastic bands snap or are not held securely, there is some risk of students being injured and so precautions should be taken. The elastic bands do not need to be stretched significantly to generate good results and so shorter universes (fewer washers) and limited stretching is encouraged. In addition, it is suggested that the ends should be fixed down securely, so measurements are consistent and the risk of injury is minimized. 

Activity 3: Draw your own circuits

Estimated time: 30 min, including graph drawing
Target age: 14–16

The relationship between the length of a conducting wire and its resistance is important for understanding direct-current circuit behaviour. However, many classroom experiments require multiple meters, calculations, large currents, and potentially overheating wires. This version is much simpler and has the added bonus that part of the experimental apparatus becomes the graph! This activity also reinforces the idea that the relationship between length and resistance will hold true for any Ohmic conductor, not just the laboratory circuit setup. They will have almost certainly calculated resistance from potential difference and current in other experiments, but, in this case, direct measurement of resistance can help them explore a pattern more quickly.

Materials

  • Soft graphite pencil (at least 6B, ideally 8B or 9B)
  • Digital multimeter that can directly measure electrical resistance up to 2 000 kΩ
  • 30 cm ruler
  • Graph paper

Procedure

  1. Using a sharpened graphite pencil and the piece of graph paper in landscape orientation, draw an x axis for a graph; this will be the wire. Go over the line 10 times in total, so the x axis is effectively a conducting ‘wire’ that is 10 pencil lines thick. Try to keep the thickness and width as even as possible; it may be necessary to sharpen the pencil halfway through. The y axis (resistance) can be drawn normally, as it is not used to collect data.
  2. Using the multimeter on the highest resistance setting (often 2 000 kΩ), place one connector at the origin and the other one at the other end of the x axis wire and record the resistance value. This will be the maximum resistance reading. Plot this value on the graph.
  3. Repeat data collection for different lengths of wire (distances along the x axis), in each case plotting the length and resistance values on the graph.
Image courtesy of James de Winter
  1. Once a full set of results is collected, draw a further 10 lines on the x axis over the previous ones. This has now effectively doubled the thickness of the wire, as it is now 20 lines thick. It is suggested to re-sharpen the pencil to ensure similar thicknesses of lines.
  2. Repeat data collection as outlined in steps 2 and 3 above.
Image courtesy of James de Winter

Discussion

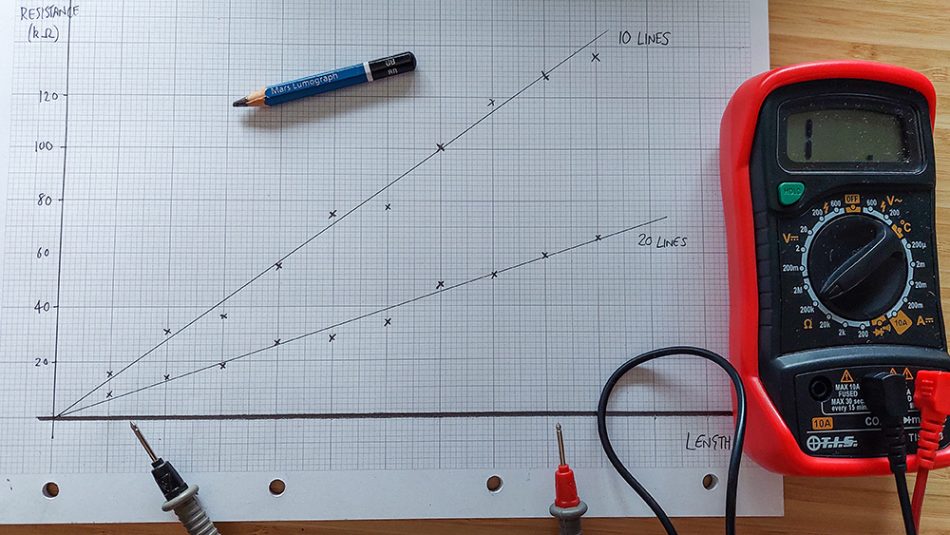
Although the data is unlikely to be perfect, students should be able to see a clear, straight-line relationship, which shows that increasing length corresponds to increasing resistance and that these are proportional.

Students can also calculate a value for resistance per unit length from the gradient of the graph. The resistance of the second, 20-pencil-line-thick wire should be approximately half that of the first one. Even if gradients are not calculated, it should be clearly seen that a thicker wire has a lower resistance for the same length. 

This experiment can be followed up with a simple demonstration of the principle behind some dimmer switches, using a 9 V battery and a light-emitting diode (LED). Shade two thick, parallel lines on a piece of paper; the distance between these lines should be the same as the distance between the terminals of a 9 V battery. Hold the battery terminals onto the wires at one end. Bend the legs of the LED, so that they touch the pencil wires and slowly slide the LED along the wires towards the battery. If connection is maintained and the LED is orientated correctly, the LED will be seen to get brighter as it moves towards the battery and dimmer as it moves away.

9 V battery standing on its contacts on two black lines drawn on a sheet of paper. Two red LEDs lying next to it, touching the lines with their contacts. One LED emitting red light.
Image courtesy of James de Winter

References

[1] A classroom activity kit from the Perimeter Institute: https://resources.perimeterinstitute.ca/products/the-expanding-universe?variant=17163100102

Resources

Author(s)

James de Winter has led the physics teacher preparation course at the University of Cambridge, UK, for many years. He is a member of the physics education research group at the University of Uppsala, Sweden, and works with the Ogden Trust to support physics teachers. He co-edited and contributed to the third edition of the Association for Science Education’s book for teachers, Teaching Secondary Physics, recently published by Hodder Education.

Review

This is an excellent article on several fronts. It dispenses with specialist equipment in favour of household items. This helps to emphasise that science isn’t confined to laboratories and helps those students who cannot ‘see’ past sophisticated equipment to the underlying physics. Activity 1 provides an accessible alternative to the usual Hooke’s Law investigation. It shows that Hooke’s Law also applies to objects in compression and replicates how scientists actually measure the stress, strain and Young’s Modulus of materials.

Activity 2 models a one-dimensional universe, which neatly demonstrates that the universe has no centre. This could lead to a discussion of other counter-intuitive ideas in physics, the difficulties of visualising them, and the use of models to explain them. For example, it is believed that the universe has no edge or boundary. To solve this, you could get students to imagine the three-dimensions of space reduced to the two-dimensions on the surface of a sphere. No matter the journey, an edge is never encountered on this surface. There is no centre and the size of the universe would increase if the sphere were allowed to expand.

Mike Follows, Physics Teacher & Head of Junior Science, King Edward’s School in Birmingham, UK

License

CC-BY
Text released under the Creative Commons CC-BY license. Images: please see individual descriptions