SI units: a new update for standards Understand article

In an update using the latest scientific research, all the basic SI units will soon be officially defined in terms of the Universe’s fundamental constants.

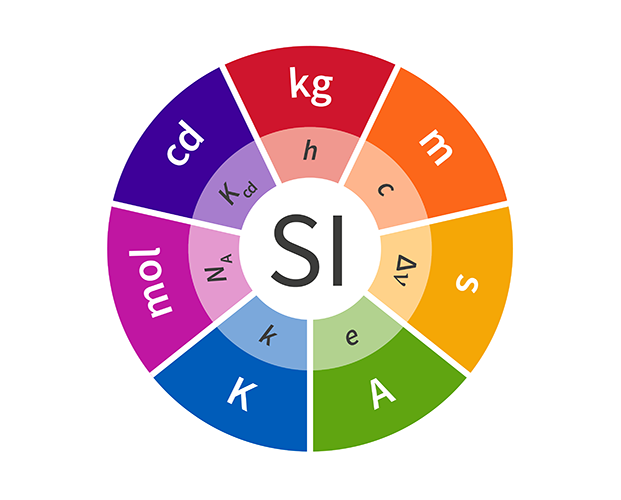
While the USA remains obstinate about using units such as miles, pounds and degrees Fahrenheit, most of the world has agreed that using units that are actually divisible by ten is a better idea. The metric system, also known as the International System of Units (or SI units), is the most comprehensive and precise system for measuring the Universe that humans have developed, comprising the seven base units for length, mass, time, temperature, electric current, luminosity and quantity.

Since the metric system was established in the 1790s, scientists have attempted to give increasingly precise definitions for these units. Some revised definitions are now due to introduced for four of these units – the kilogram (kg), kelvin (K), ampere (A) and mole (M) – bringing them into line with the other units by providing definitions based on natural constants. The updated definitions will be adopted internationally on World Metrology Day, 20 May 2019. After this update, every base unit in the metric system will be defined using the fundamental constants of the Universe.

Metre (distance)

Starting in 1799, the metre was defined by a prototype metre bar, which was just a platinum bar. Physicists eventually realised that distance could be defined by the speed of light (c), which has been measured with an accuracy to one part in a billion using an interferometer (the same type of detector that was used recently to discover gravitational waves). The metre (m) is currently defined as the distance travelled by light (in a vacuum) for 1/299 792 458th of a second and will remain effectively unchanged after the update.

Kilogram (mass)

For over a century, the standard kilogram has been a small platinum-iridium cylinder housed at the Bureau International des Poids et Mesures (BIPM), near Paris, France. But even its precise mass fluctuates due to factors such as accumulation of microscopic dust. The latest update redefines the kilogram (kg) by setting the value of Planck’s constant to exactly 6.626070040 x 10^-34 kg m² s^-1. Planck’s constant is the smallest possible amount of (quantised) energy. This fundamental value, which is represented by the letter h, is integral to calculating energies in particle physics.

Second (time)

The earliest definition of seconds was based on divisions of time between full moons. Later, seconds were defined by solar days, and eventually the time it took Earth to orbit around the Sun. Today, seconds (s) are defined by atomic time, which is precise to one part in 10 billion. Atomic time is based on the periods of radiation produced and absorbed by atoms, called the ‘hyperfine transition frequency’ (Δ_ν). One second is currently defined as 9 192 631 770 periods of the radiation for a caesium-133 atom and will remain effectively unchanged.

Kelvin (temperature)

The kelvin temperature scale starts at the coldest possible state of matter. Currently, the kelvin (K) is defined by the triple point of water – the temperature at which water can exist simultaneously as a solid, liquid and gas. The triple point is 273.16 K, so one kelvin is 1/273.16 of the triple point. But water can never be completely pure, and impurities can influence the triple point. In May 2017, a team of German physicists at the Physikalisch-Technische Bundesanstalt made the most precise measurements yet of the Boltzmann constant. Denoted by the symbol k, the Boltzmann constant is ubiquitous throughout physics calculations that involve temperature and entropy, and links the movement of particles in a gas (the average kinetic energy) to the temperature of the gas. These results are now being used to redefine units of temperature by setting the value of Boltzmann’s constant to exactly 1.38064852 x 10²³ joules (J) per kelvin. 

Ampere (electric current)

André-Marie Ampère (1775–1836), who is often considered the father of electrodynamics, has the honour of having the basic unit of electric current named after him. Until now, the ampere (A) has been defined by the amount of current required to produce a force of 2 x 10^-7 newtons (N) for each metre between two parallel conductors of infinite length. Naturally, it’s a bit hard to come by things of infinite length, so the updated definition will instead define amperes by the fundamental charge of a particle. This new definition relies on the charge of the electron, e, which will be set to 1.6021766208 x 10^-19 ampere seconds.

Candela (luminosity)

The last of the base SI units to be established, the candela measures luminosity – what we often refer to as brightness. Early standards for the candela used a phenomenon from quantum mechanics called black body radiation, which is the light that all objects radiate as a function of their temperature. Currently, the candela (cd) is defined more fundamentally as 1/683 watt (W) per square radian at a frequency of 540 x 10¹² hertz (Hz) over a certain area, a definition that will remain effectively unchanged. Hard to picture? A candle, conveniently, emits about one candela of luminous intensity. 
 

Mole (quantity)

Different from all the other base units, the mole measures quantity alone and is just a number. Over hundreds of years, scientists starting from Amedeo Avogadro (1776–1856) worked to better understand how the number of atoms was related to mass, leading to the current definition of the mole (M): the number of atoms in 12 grams (g) of carbon-12. This number, which is known as Avogadro’s constant (N_A), is about 6 x 10²³. To make the mole more precise, the new definition will set Avogadro’s constant to exactly 6.022140857 x 10²³, decoupling it from the kilogram.

Acknowledgement

This is an edited version of an article first published in Symmetry online magazine on 7 November 2017^w1. 

Download

Download this article as a PDF