The numbers game: extending the periodic table Understand article
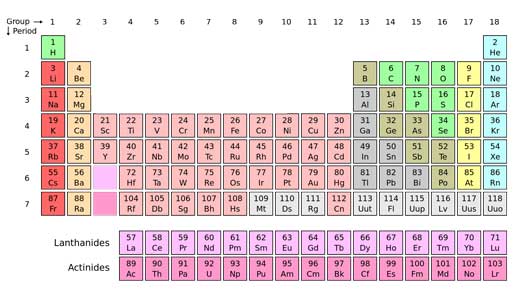
Until a few centuries ago, people believed that the world was made only of earth, air, water and fire. Since then, scientists have discovered 118 elements and the search is on for element 119.

image source: Wikimedia
Commons
In space-age labs across Europe, researchers are working together to discover new elements. If they succeed, they will join the club of scientists who have rewritten the periodic table.
The Ancient Greeks might not have been right about there being just four elements – earth, air, fire and water – but they were onto something: elements are the ingredients of everything that surrounds us, bound to each other in compounds and mixed together in different proportions. But while compounds exist in kaleidoscopic variety, elements are pretty simple, and there are so far only 118 elements known to sciencew1. Discovering a new one is a big deal.
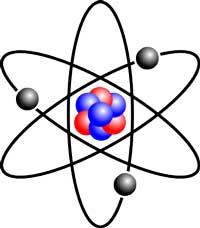
Image courtesy of Halfdan;
image source: Wikimedia
Commons
Atoms, the building blocks of matter, are all made of the same simple components: tiny particles called protons and neutrons, and even tinier electrons orbiting them. The number of protons in an atom – its atomic number – defines what element it is. An atom of oxygen, for example, has eight protons, eight neutrons (usually) and eight electrons, whereas the heaviest elements can have more than a hundred of each.
* * *
The Russian chemist Dmitri Mendeleev knew none of this when, in 1869, he arranged the elements into a table based on their atomic weight. He quickly saw patterns emerge: in particular, columns grouped together elements with startlingly similar properties. For example, potassium, rubidium and caesium, three metals that react violently with water, are stacked one above the other.
At first, Mendeleev’s table had a problem: it was full of gaps. Between zinc and arsenic, for instance, there seemed to be two elements missing. But he boldly predicted that these holes would be filled with newly discovered elements, and used his table to forecast what their properties would be. And he was right: the gap was soon filled by gallium and germanium.

published in 1869.
Click on image to enlarge.
Public domain image; image
source: Wikimedia Commons
With a few refinements and modifications, the table that Mendeleev created became what we use to this day: the periodic tablew1, something so basic that we never stop to think that it had to be invented.
In the following decades, chemists raced to fill the remaining gaps. Along the way, they also discovered why the periodic table works: the rows and columns mirror the way electrons are arranged in their orbits in different elements, and the electrons in turn dictate many of the elements’ properties.
In 1945, the last gap in the table was filled. Had science at last discovered all the elements? Curiously, the answer is both yes and no. All the elements that exist naturally on Earth were known. But – and it’s a big but – there was nothing to say that new elements could not be created artificially, tagged onto the end of the periodic table beyond element number 92, uranium.

Public domain image; image
source: Wikimedia Commons
So with the development of atomic research in the 1940s, just as the last holes in the table were being filled, a trickle of new lab-created elements started to join the end of the periodic table, bringing us up to the 118 elements known today. Nobody knows how many are yet to be discovered.
What is known, though, is that creating new elements is getting harder. Today, you need the most advanced labs in the world if you are to stand a chance: the easy ones have all been found.
* * *
Known by the tongue-twisting name ununennium, the predicted element that an international team is focusing on today is likely to be the hardest yet.

scientists plan to fire an
intense beam of titanium
atoms into berkelium.
Image courtesy of stock
photos for free.com
The team, co-ordinated by the GSI Helmholtz Centre for Heavy Ion Research (GSI Helmholtzzentrum für Schwerionenforschung), in Germany, and involving about 20 research centres from around the world, plans to create element 119. Their method sounds deceptively simple: fire a beam of titanium atoms (atomic number 22) into some berkelium (97). Add the two together and – eureka! – you get 119.
Of course it’s not so easy.
First of all, highly radioactive berkelium doesn’t exist in nature either: it first has to be created in a nuclear reactor. Moreover, it’s ludicrously hard to actually smash the elements together.
Image courtesy of Shape;
image source: Wikimedia
Commons
“It is extremely difficult to create intense titanium beams. To accomplish this, we have secrets that we will not share with others,” explains Professor Jon Petter Omtvedt, one of the team members. “We shall bombard the plate with a beam of five trillion [5 x 1012] titanium atoms per second. […] The probability of a direct hit [between the atoms] is extremely low. When the atoms collide with each other on rare occasions, they are usually merely shattered or partly destroyed in the collision. However, less than once a month, we will get a complete atom.”

members Professor
Christoph Düllmann and Dr
Alexander Yakushev in front
of the experimental setup.
With the aid of a particle
accelerator, titanium ions
are accelerated to close to
the speed of light, after
which they pass along the
silver tube on the left and
smash into a target made of
berkelium (in the yellow-
striped box in the centre).
Using three magnets (red
boxes on the right), the
resulting ununennium ions
are separated from all
other particles, after which
they enter the detector,
where their decay can be
registered.
Image courtesy of G Otto / GSI
That’s like winning the lottery jackpot by buying enough tickets to guarantee a win. It’s slow and inefficient, but it’s a numbers game, and you’ll get there eventually.
But there’s another problem. All the heavy elements are radioactive: their atoms break down into lighter ones over time, releasing radiation. And the heaviest elements discovered have all been incredibly unstable. Ununoctium (element 118) decomposes within milliseconds of being created; ununennium may be even shorter-lived.
It’s not that they’re dangerous – the amounts are so tiny that the dose of radiation is safe. But it makes it difficult to study the element you’ve just created: you can’t drop it in a test-tube or heat it in a Bunsen burner flame, because you only ever have a single atom at a time and for just a fraction of a second.
The team’s solution is to create the ununennium with the aid of a particle accelerator, then fire it into a detector and look for the tell-tale signs of ununennium nuclei disintegrating – radiation and the atoms that it breaks up into – rather than the ununennium itself.
It’s a clever solution, but it leaves one of the team’s ambitions out of reach: they would love to be able to study how atoms of these exotic elements react with each other. But that’s probably never going to be possible, at least not using any kind of technology we can imagine today.
But if your job is to create new elements for a living, beating lottery jackpot odds along the way, ‘impossible’ might sound like a challenge….
Acknowledgement
The editors of Science in School would like to thank Professor Christoph Düllmann from the GSI Helmholtz Centre for Heavy Ion Research for his help with this article.
Web References
- w1 – The International Union of Pure and Applied Chemistry (IUPAC) is the official body that decides whether an element has been discovered. The IUPAC periodic table includes all elements from 1 to 112, as well as elements 114 and 116. Elements 113, 115, 117 and 118 are not officially recognised by IUPAC, although claims have been made in the scientific literature about the discovery of these elements.
Resources
- Two press releases from the University of Oslo, Norway, provide more information on the hunt for ununennium:
- The University of Nottingham, UK, has created a website with videos relating to each of the elements in the periodic table. For a review of the website, see:
- Walsh M (2012) Review of the Periodic Table of Videos website. Science in School 24.
- The website of the UK’s Royal Society of Chemistry offers an interactive version of the periodic table, with all 118 known elements.
Review
After a brief summary of the creation and evolution of the periodic table, this article introduces current research to discover new elements. It could be used in chemistry and physics lessons, particularly when studying nuclear chemistry, atomic physics or the history of science. The article could also be used to discuss the scientific method, the velocity of scientific progress, the difficulties that researchers encounter and the usefulness of basic research.
History of science is a topic rarely seen in secondary school and it can be very useful to make science more appealing to students, especially to those more interested in the humanities. This article could be used to demonstrate the links between the sciences and humanities.
Potential comprehension questions include:
- According to Ancient Greeks, how many elements were there?
- What is the atomic number?
- How many elements does the periodic table currently comprise?
- Describe the method used by the team to try to discover new elements. What are the problems associated with this method?
Mireia Güell Serra, Spain