Galileo e le lune di Giove: esplorando il cielo notturno del 1610 Teach article
Tradotto da Paolo Sudiro. Imparate come voi e i vostri studenti potete usare la matematica per studiare le lune di Giove.

(Justus Sutermans, 1636).
immagine di pubblico dominio;
font dell’immagine: Wikimedia
Commons
In una notte di gennaio del 1610, Galileo Galilei osservò Giove attraverso il suo telescopio e vide tre oggetti vicino al pianeta che pensò fossero delle stelle. Continuò le osservazioni per circa due mesi e infine si rese conto che, in effetti, c’erano quattro “stelle” che cambiavano le loro posizioni intorno a Giove. Galileo concluse che le “stelle” erano in realtà dei pianeti che orbitavano intorno a Giove – gli Astri Medicei, come li chiamò al tempo, ma che noi oggi conosciamo come le lune Galileiane in onore del loro scopritore (figura 1).
“Ma il fatto più straordinario, che soprattutto ci ha spinto ad informare tutti gli Astronomi e i Filosofi, è la scoperta di quattro Astri Erranti, che nessuno prima di noi aveva mai conosciuto ne’ osservato…”
Galileo Galilei, Sidereus Nuncius (Il Messaggero delle Stelle, 1610)

Galileiane Io, Europa,
Ganimede e Callisto (Giove
non è alla stessa scala dei
satelliti).
Immagine gentilmente
concessa da NASA Planetary
Photojournal
La scoperta di Galileo è alla base di un progetto che ho ideato per i miei studenti di fisica dell’ultimo anno delle superiori (17-18 anni di età) quando insegno l’argomento del moto armonico semplice. Il progetto è costruito su un’attività simile che ho precedentemente sviluppato sul moto della luna Galileaiana Io (Ribeiro, 2012). Il presente progetto è basato sull’indagine ed ha lo scopo di impegnare gli studenti con un’ampia varietà di procedimenti scientifici – dall’esplorazione del contesto storico alla raccolta ed analisi dei risultati sperimentali e la comunicazione delle loro conclusioni ad altri.
Lo scopo del progetto è che i vostri studenti dimostrino che Galileo aveva ragione quando ha affermato che le “stelle” vicino a Giove erano in effetti i satelliti del pianeta. Per fare questo, gli studenti raccolgono dati sul movimento delle lune usando una simulazione al computer e quindi verificano che il movimento ha le caratteristiche del moto armonico semplice, con Giove al centro. Alla fine del progetto, gli studenti preparano un rapporto (un documento o una presentazione) per descrivere quello che hanno scoperto e l’intero procedimento che hanno seguito – e, idealmente, lo condividono con studenti di altri paesi così da imparare a comunicare internazionalmente un lavoro scientifico.
La durata del progetto varia in funzione di come gli insegnanti decidono di affrontarlo. Personalmente, ho passato quattro mesi a lavorare sul progetto coi miei studenti; ma, se non avete il tempo di completare l’intero progetto con i vostri studenti, potete selezionare singole attività.
Il moto armonico semplice ed il moto circolare uniforme
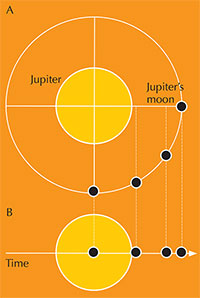
lune Galileiane intorno a
Giove: A) visto da sopra il
piano dell’orbita e B) visto
dalla Terra (visto
parallelamente al piano dell’
orbita). I punti neri indicano
le posizioni delle lune
Galileiane a intervalli di
tempo costanti. Cliccare sull’
immagine per ingrandirla.
Immagine gentilmente
concessa da Carla Isabel
Ribeiro
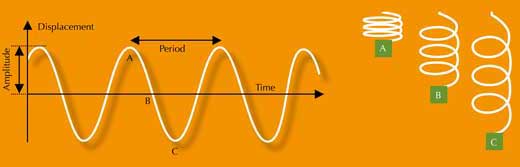
Immagine gentilmente concessa da Nicola Graf
Moto armonico semplice (MAS) è il termine con cui vengono descritti i movimenti periodici regolari come il dondolio del pendolo, o l’oscillazione di un oggetto collegato ad una molla. Tracciando questi movimenti su un grafico (distanza dal punto centrale rispetto al tempo) si produce la figura caratteristica di una sinusoide (figura 2).
Il MAS può venire interpretato come la proiezione lungo un asse di un oggetto che si sta muovendo di moto circolare uniforme (MCU). Per esempio, immaginate un oggetto che si stia muovendo in cerchio sul piano orizzontale. Se guardiamo questo piano a “livello occhi” (equivalente ad una proiezione sull’asse x), vediamo un movimento avanti e indietro esattamente uguale a quello di un oggetto oscillante collegato ad una molla. Solo quando guardiamo il moto dall’alto il movimento ci appare circolare.
Questa relazione tra MAS e MCU può venire applicata alle lune Galileiane viste dalla Terra: il loro movimento sembra essere un MAS a cause della proiezione del loro MCU intorno al pianeta sulla nostra direzione di osservazione (figura 3). (Le orbite sono leggermente eccentriche, ma solo di una piccola entità, così si può considerare che le lune abbiano un’orbita circolere e si muovano a velocità costante).
La cosmologia al tempo di Galileo

geocentrico del cosmo nel
XVI secolo, descritto nella
Cosmographia di Bartolomeu
Velho (1568). Cliccare sull’
immagine per ingrandirla.
immagine di pubblico dominio;
font dell’immagine: Wikimedia
Commons
Le osservazioni di Galileo sulle lune di Giove vennero fatte durante un’epoca di transizione scientifica, dal modello geocentrico (centrato sulla Terra; figura 4) di Aristotele e della Chiesa Cattolica a quello eliocentrico (centrato sul Sole).
Galileo, ovviamente, avrebbe aderito esplicitamente al modello eliocentrico alcuni anni più tardi, in una sfida diretta alla dottrina Cattolica. Comunque, le sue osservazioni al telescopio, pubblicate nel suo libro Sidereus Nuncius (Il Messaggero delle Stelle) nel 1610, provocarono già degli attriti perché contraddicevano gli insegnamenti di Aristotele. Nel modello di Aristotele ogni cosa nel cosmo orbita intorno alla Terra – così l’idea di lune orbitanti intorno al pianeta Giove non concordava con questo.
Il progetto passo per passo
Passo 1: la cosmologia del XVII secolo
Chiedete ai vostri studenti di fare una ricerca sulle teorie cosmologiche comunemente accettate in Europa agli inizi del XVII secolo. Quali effetti potevano avere avuto su Galileo, le sue osservazioni e le sue conclusioni? Gli studenti dovrebbero anche leggere degli estratti dal Sidereus Nunciusw1, nel quale Galileo descrive le sue osservazioni e conclusioni.
Passo 2: scegliere il software planetario
Dovrete scaricare il programma planetario gratuito Stellariumw2 o una simulazione simile. Quindi dividete i vostri studenti in quattro gruppi e assegnate a ciascun gruppo una delle quattro lune Galileiane (Io, Callisto, Ganimede o Europa).
Passo 3: seguire le lune di Giove

Chiedete ai vostri studenti di usare Stellarium per indagare la posizione di ciascuna delle loro lune nel tempo: in una tabella ciascun gruppo dovrà registrare lo scostamento (x) – la distanza della loro luna dal centro di Giove – in momenti successivi (t). Dovranno anche trovare lo scostamento massimo (A) della luna dal centro del pianeta.
Le misurazioni devono essere eseguite ad intervalli differenti per le quattro lune, in funzione della loro distanza dal pianeta e, quindi, del loro periodo orbitale. Gli studenti dovrebbero procedere per prove ed errori in modo da trovare l’intervallo più appropriato per la loro luna. Il loro obiettivo è quello di ottenere almeno 10 misurazioni, una delle quali dovrebbe essere A.

Per esempio, Io è la luna più vicina a Giove, il che significa che orbita più velocemente. Se gli studenti eseguono le loro misurazioni a intervalli di 1 h i dati non saranno sufficienti; 15 min sarebbero più appropriati. Per una delle lune più distanti da Giove , intervalli di 15 min fornirebbero più dati del necessario, così si dovrebbero usare intervalli più lunghi.
Per trovare il centro del pianeta su Stellarium, i vostri studenti possono usare i riferimenti rossi intorno a Giove (figura 5) per tracciare due linee passanti per il centro. Per trovare la distanza da quel punto alla luna che viene studiata possono utilizzare un programma di immagine, o stampare uno screenshot e misurare la distanza con un righello.

Giove e le sue lune Europa
(A) e Io (B) con il programma
gratuito Stellarium. Cliccare
sull’immagine per
ingrandirla.
Immagine gentilmente
concessa da Stellarium
Passo 4: verificare le conclusioni di Galileo
Il quarto e più complicato passo è la dimostrazione da parte degli studenti che Galileo era nel giusto quando ha concluso che il MAS che aveva osservato era prodotto dal MCU di una luna intorno al suo pianeta.
Per trovare il periodo orbitale T delle loro lune gli studenti avranno bisogno delle equazioni matematiche per il MAS:
x = A × sin(ω t + φ) (1)
dove w è la frequenza angolare e j è una costante (la costante di fase), insieme con l’equazione che collega w e T:
ω = 2π / T
dove x è lo scostamento, A l’ampiezza o scostamento Massimo del moto, t è il tempo e j è una costante (la costante di fase).
L’equazione (1) può essere trasformata nell’equazione lineare (2), perciò:
x = A × sin(ω t + φ) (1)
→ x / A = sin(ω t + φ)
→ arcsin(x / A) = ω t + φ
Since ω = 2π / T
→ arcsin(x / A) = (2π/ T)t + φ (2)
Se i vostri studenti osservano un oggetto che si comporta seguendo l’equazionie (2) – che descrive il MAS – allora è ragionevole concludere che sta orbitando attorno al pianeta come una luna.
Poiché l’equazione (2) è lineare, possiamo vedere che se i vostri studenti usano i dati da loro raccolti al passo 3 per tracciare un grafico di arcsin(x / A) rispetto a t, il gradiente sarà 2p / T, dal quale possono facilmente calcolare il periodo orbitale T. La costante di fase della luna, j, è l’intercetta sull’asse y. La figura 6 mostra un esempio di un grafico che i vostri studenti potrebbero tracciare utilizzando i dati della luna Europa.
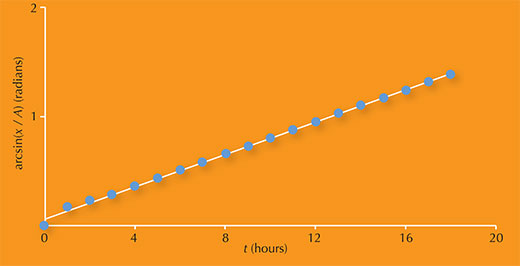
Immagine gentilmente concessa da Carla Isabel Ribeiro
Il grafico qui sopra ha un gradiente di 0.0741.
Poiché il gradiente è uguale a to 2p / T, ne segue che:
2π / T = 0.0741
→ T = 2π / 0.0741
= 84.8 h
Gli studenti matematicamente più abili potrebbero procedure ad un’analisi di regressione dei dati per verificare la “bontà della correlazione” per l’equazione (2). Il valore ottenutio nel caso di Europa (R2 = 0.998) dimostra che i dati concordano fedelmente con l’equazione e perciò conferma che l’oggetto si comporta come una luna in orbita.
Il valore atteso per Europa è di circa 3.55 giorni (85.2 h), che è abbastanza simile al valore calcolato sopra. La differenza tra i due valori può essere un buon punto di partenza per una discussion sull’accuratezza dei risultati sperimentali. Che cosa potrebbere essere andato male? Si trattava forse di errori casuali o sistematici?
In questo caso l’errore può essere stato causato dalla misurazione di A, poiché la posizione della luna veniva simulata ad intervalli di 1 h e lo scostamento massimo potrebbe essere stato raggiunto tra due misure. Voi potreste chiedere ai vostri studenti di suggerire dei metodi per minimizzare l’errore.

di Venzia come utilizzare il
suo telescopio(HJ Detouche,
1754) Cliccare sull’immagine
per ingrandirla.
immagine di pubblico dominio;
font dell’immagine: Wikimedia
Commons
Passo 5: presentazione dei risultati
L’ultimo passo per ciascun gruppo è la presentazione del loro lavoro, descrivendo l’intera indagine e presentando i loro risultati. Nella scienza è importante comunicare, così potete fare in modo che i vostri studenti facciano le loro presentazioni ad un’altra classe, o forse come parte di una esibizione o un open day della scuola. Gli studenti dovrebbero pensare al metodo migliore per comunicare il loro lavoro. Come potrebbero semplificarlo per renderlo comprensibile ad altri? Quali immagini potrebbero utilizzare per aiutarli a spiegare quello che hanno fatto?
Più ambiziosamente, potreste addirittura avviare una collaborazione con una scuola di un altro paese. Gli scienziati talvolta devono comunicare in lingue straniere – spesso, ma non sempre, in inglese. Sulla base di questo progetto spero di riuscire ad avviare una collaborazione internazionale attraverso la rete eTwinningw3. A scala più ridotta, sarei felice di sapere di altre scuole che volessero lavorare insieme al progetto.
References
- Ribeiro CI (2012) Io and its simple harmonic motion. Physics Education 47: 268-270. doi: 10.1088/0031-9120/47/3/F04
Web References
- w1 – Scaricate una recente traduzione inglese del Sidereus Nuncius, il famoso lavoro di Galileo nel quale descrive le scoperte da lui fatte col telescopio. Le pagine 17 e 18 contengono le sue osservazioni sulle lune di Giove per le date descritte in questo progetto.
-
Anche l’edizione originale è disponibile online.
-
- w2 – Stellarium, il simulatore planetario utilizzato nel progetto, può essere scaricato gratis.
- w3 – Il sito web eTwinning promuove la collaborazione scolastica in Europa attraverso l’utilizzo delle tecnologie informatiche e di comunicazione (ICT). Disponibile in 23 lingue, ha quasi 50000 membri e oltre 4000 progetti registrati tra due o più scuole in tutta Europa.
Resources
- Il sito web Physclips offre una chiara spiegazione del moto armonico semplice, con video e animazione.
- Il sito web Solar System Exploration della NASA fornisce informazioni aggiornate su Giove e le sue lune, incluse le missioni spaziali.
- Per un articolo che descrive un simile progetto di esplorazione delle lune Galileiane, utilizzando un telescopio attrezzato con una fotocamera a dispositivo ad accoppiamento di carica (CCD), vedete:
-
de Moraes IG, Pereira JAM (2009) Using simple harmonic motion to follow the Galilean moons – testing Kepler’s third law on a small system. Physics Education 44: 241. doi: 10.1088/0031-9120/44/3/002
-
L’articolo può essere scaricato gratuitamenete dal sito web dell’Università della Piccardia, in Francia.
-
- Il Progetto CLEA (Contemporary Laboratory Experiences in Astronomy), del Gettysburg College, USA, offre esercitazioni di laboratorio che illustrano le tecniche astronomiche moderne. Ciascun esercizio consiste in uno specifico programma per computer, un manuale per lo studente ed una guida tecnica per l’insegnante. Molti degli esercizi coinvolgono le lune di Giove.
Review
Questo articolo suggerisce un nuovo metodo basato sull’indagine per l’insegnamento del moto armonico semplice: gli studenti usano le loro conoscenze di matematica, fisica e di tecnologia informatica e delle comunicazioni per caratterizzare il moto delle lune di Giove. Raccolgono i dati da un programma software, li elaborano e tracciano dei grafici, in particolare delle funzioni del seno e dell’arco di seno, per calcolare i periodi orbitali delle lune.
La natura interdisciplinare dell’articolo serve a rendere la scienza più piacevole. iInoltre l’attività sviluppa abilità non tecniche come la presentazione e comunicazione dei risultati. Attraverso un collegamento ad un progetto internazionale gli studenti hanno l’opportunità di condividere i loro risultati non solo con altri membri della loro classe, ma con studenti di diversi paesi.
Corina Toma, Scuola Superiore di Scienze Informatiche “Tiberiu Popoviciu” Cluj Napoca, Romania





