Măsurători inteligente ale cerurilor Teach article

Tradus de Mircea Băduţ. Încurajați-vă elevii să-şi folosească smartphone-urile pentru câteva măsurători astronomice.

Unde anume te afli în acest moment? O modalitate de a afla ar fi să utilizezi funcția de poziționare prin satelit (cunoscută şi sub numele de GPS) a telefonului tău mobil. În trecut, ar fi trebuit să te bazezi pe stele pentru a afla – mai ales dacă erai un marinar pe oceane, într-un peisaj fără particularităţi.

În acest articol, vom descrie câteva din primele practici ale navigației bazate pe stele, și vom arăta modul în care aceste tehnici tradiționale pot fi reproduse la clasă folosind aplicații simple de pe smartphone. Elevii pot utiliza apoi funcția GPS de pe smartphone pentru a verifica acuratețea muncii, acesta înainte de a lua în calcul şi sursele de erori posibile.

Potrivite pentru elevii cu vârste între 14-18 ani, cele două activități leagă istorie, astronomie, geografie și matematică: determinarea latitudinii (figura 1) cu ajutorul Soarelui, și determinarea latitudinii folosind Steaua Polară. Din secțiunea de materiale suplimentare se pot descărca detaliile unei inedite activități de colaborare între școli derulate pentru calcularea circumferinței Pământului. Cele trei activități necesită un pic mai mult decât un smartphone și nu mai mult de o oră fiecare.

Determinarea latitudinii locale folosind altitudinea Soarelui

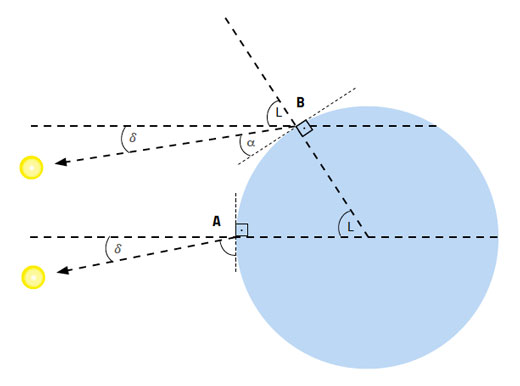
„Când este amiază?” poate părea o întrebare nefirescă. Dar este amiaza chiar la ora12 ziua? Strict vorbind, amiaza solară are loc atunci când Soarele traversează meridianul tău, sau când trece peste o linie de longitudine, și de obicei, ne va apărea să fie mai la nord sau mai la sud. Amiaza se întâmplă atunci când Soarele se află în punctul său cel mai înalt pe cer și umbrele sunt cele mai scurte. Şi acesta este momentul în care poziția Soarelui poate fi folosită pentru a vă determina latitudinea, sau distanța unghiulară faţă de planul ecuatorului.

Cum funcţionează acest lucru? Să presupunem că ne aflăm la echinox (aproximativ pe 20 martie sau pe 23 septembrie), când planul ecuatorului trece chiar prin centrul Soarelui (figura 2).

• A: Imaginaţi-vă că staţi pe ecuator, la latitudinea 0°, la amiază: Soarele este chiar deasupra. Dacă aţi măsura altitudinea Soarelui (unghiul său de elevaţie deasupra orizontului), aţi găsi că ea are 90° (figura 3A). Scăzând acest număr din valoarea 90° obţineţi 0°, adică latitudinea curentă.

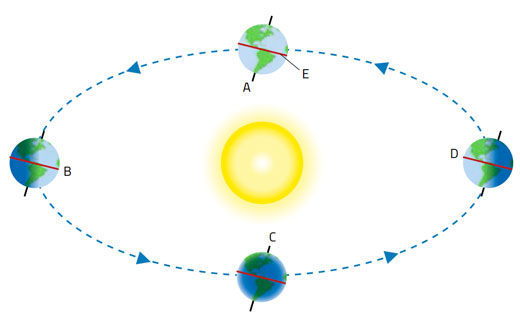
(Am afirmat anterior că la amiază Soarele este de obicei fie mai la nord fie mai la sud. La echinox, el este chiar deasupra.)

• B: Să presupunem că în acelaşi moment un prieten se află la polul Nord sau la polul Sud (latitudini de 90° N sau de 90° S). El ar vedea că Soarele se află exact la orizont, deci la o altitudine de 0° (figura 3B). Scăzând 0° din valoarea 90° obţineţi 90°, aceasta fiind latitudinea la care se află acel prieten.
• C: Un alt prieten se află pe acelaşi meridian dar la o latitudine de 30° N. Fiind pe acelaşi merdian, acolo este tot amiază, însă el observă Soarele la o altitudine de 60° desupra orizontului (figura 3C). Scăzând această valoare din 90° obţinem 30°: aceasta este latitudinea la care se află prietenul.

Latitudinea = 90° – altitudinea Soarelui la amiază, în data echinoxului.                        (Ecuaţia 1)

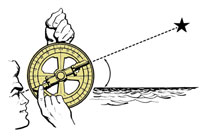
Cum putem folosi în practică aceste cunoștințe? În secolul 15 şi la începuturile secolului 16, mulți navigatori foloseau astrolabul marinarului pentru a măsura altitudinea unghiulară a Soarelui și astfel calculau latitudinea navei lor. Astrolabul marinăresc era, în esență, un înclinometru: suspendat în plan vertical, el era îndreptat spre un corp ceresc, precum Soarele. O alidadă rotativă integrată în dispozitiv (având o scală asemănătoare raportorului de la geometrie) era folosită pentru a citi direct altitudinea corpului ceresc (figura 4).

Deşi astrolabul marinăresc ar fi relativ simplu de construit^w2, ne vom folosi, cu uşurinţă, de un smartphone pentru a măsura altitudinea Soarelui, cu ajutorul unei aplicații înclinometru. Însă înainte de aceasta, trebuie să rafinăm metoda, astfel încât calculele noastre să funcționeze în orice zi a anului.

Din cauza înclinării axei de rotație a Pământului (23,45°), precum și a faptului că Pământul se rotește în jurul Soarelui, doar la echinocții Soarele ne apare direct deasupra ecuatorului. Începând de la echinocțiul din martie, poziția Soarelui la amiază se mută tot mai la nord de ecuator, atingând unghiul maxim de + 23,45° la solstițiul din iunie, şi revenind la 0° la echinocţiul din septembrie, după care se deplasează la sud de ecuator până ce ajunge la -23,45° la solstițiul din decembrie. Acest unghi se numeşte declinația Soarelui (figura 5).

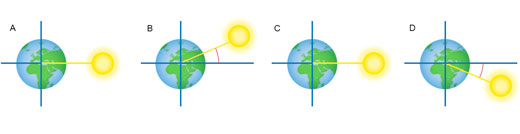
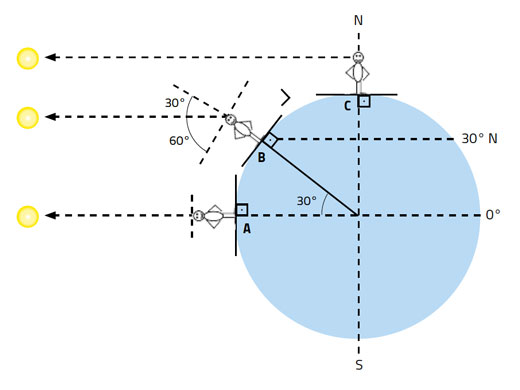
Astfel, altitudinea unghiulară a Soarelui la amiază, pe care navigatorii de pe vremuri o măsurau cu astrolabul marinăresc, și pe care acum o putem măsura cu un smartphone, depinde atât de ziua din an – și, prin urmare, de declinația Soarelui – cât și de latitudinea la care ne aflăm (figura 6):

Altitudinea Soarelui la amiază = 90° + declinaţia – latitudinea                        (Ecuaţia 2)

Sau, după rearanjare:

Latitudinea = 90° – altitudinea Soarelui la amiază + declinaţia            (Ecuaţia 3)

Pentru a determina declinaţia Soarelui, navigatorii de pe vremuri foloseau tabele cu date sau astrolabe marinăreşti complicate la care declinaţia Soarelui era marcată pe un disc rotitor. Putem astăzi obţine aceeaşi informaţie printr-o aplicaţie de tip planetarium, după care putem măsura elevaţia Soarelui pentru a ne determina latitudinea.

Materiale

Fiecare grup de elevi va avea nevoie de:

• Un smartphone având instalate aplicaţii de tip înclinometru şi planetarium
• Un pai de băutură răcoritoare
• Bandă adezivă
• Nivelă (opţional)

Procedura de lucru

Pentru a determina latitudinea curentă, elevii trebuie să:

1. Folosească banda adezivă pentru a prinde paiul de-a lungul muchiei smartphone-ului (figura 7). Ansamblul acesta va constitui alidada.
2. Utilizeze aplicaţia de planetarium pentru a determina timpul local al amiezei solare (ora locală la care Soarele se află cel mai sus) şi declinaţia Soarelui.

În funcţie de locaţia curentă şi de fusul orar, amiaza solară poate fi cel mai devreme la 11:30 am, şi, datorită decalajului orei de vară, poate fi cel mai târziu la 1:30 pm.

3. Ansamblul ‘smartphone – pai de băut’ este orientat cu paiul spre Soare. Smartphone-ul este corect aliniat când umbra paiului este cea mai mică (figura 7).
4. Folosind aplicaţia înclinometru, se citeşte unghiul elevaţiei Solare.
5. Se aplică ecuaţia 2 pentru a afla latitudinea locală.

Alternativ, pentru a facilita elevilor să orienteze mai riguros smartphone-ul către Soare şi astfel să măsoare mai precis elevaţia Soarelui, se poate construi un suport plasat pe un tripod. Detalii privind construirea ansamblului se pot găsi pe web^w3.

Discuţii

Cereţi elevilor să compare rezultele obţinute cu latitudinea exactă furnizată de funcţia GPS a smartphone-ului sau cu cea obţinută prin aplicaţia planetarium. Cât de precise sunt valorile calculate? Care ar putea fi sursele de eroare?

Desigur, precizia rezultelor depinde în primul rând de acurateţea cu care au lucrat elevii, de exemplu, de cât de bine a fost aliniat paiul pe muchia smartphone-ului sau de cât de reuşită a fost minimizarea umbrei paiului. Pentru o precizie ridicată, măsurătorile trebuie efectuate la amiază, dar câteva minute mai devreme sau mai târziu nu vor mult afecta estimarea, deoarece, când este la punctul său maxim de pe boltă, Soarele îşi schimbă cel mai lent altitudinea.

Smartphone-urile îşi pot măsura unghiul de înclinare cu o precizie de 0,1°, ceea ce nu-i rău. Însă ar fi interesant de calibrat aplicaţia înclinometru cu o nivelă, pentru a vedea dacă valoarea de 0,0° corespunde cu adevărat orizontalei.

Aţi putea cere elevilor să-şi spună opinia privind faptul că, deşi latitudinea s-a putut determină încă din atichitate, longitudinea a devenit posibil de măsurat de-abia în secolul al 18-lea.

Răspunsul vine din rotaţia Pământului: 360° într-o zi sau 15° într-o oră. Astfel, prin compararea timpului local, cu timpul de la un punct de referință având longitudinea cunoscută, ar fi posibil să se determine longitudinea. Ora locală ar putea fi estimată din poziţia Soarelui, dar neajunsul fost timpul corespunzător punctului de referință: un ceas capabil să urmărească timpul cu precizie, mai ales la bordul unei nave în mișcare, a fost inventat de-abia în 1759, de John Harrison.

Determinarea latitudinii locale folosind altitudinea Stelei Polare

În activitatea de clasă anterioară am măsurat altitudinea Soarelui la amiaza locală (atunci când Soarele traversează meridianul local). În acel moment Soarele apare a fi poziţionat mai la sud sau mai la nord. Dacă elevii ar fi fost nevoiţi să calculeze latitudinea lor de la Soare în alte momente ale zilei, s-ar fi obţinut rezultate foarte inexacte. Din fericire, există o altă metodă care nu depinde de timp atât de critic, însă ea funcționează numai în emisfera nordică și trebuie să se facă după lăsarea întunericului, bazându-se pe Polaris, Steaua Nordului (Alpha Ursae Minoris).

În timp ce pozițiile altor stele par să se schimbe pe durata nopții, Polaris ne apare că rămâne fixată în partea de nord (figura 8), deoarece poziția ei se află pe direcţia axei de rotație a Pământului. Dacă te-ai afla la Polul Nord (latitudine 90° N), Polaris ar apărea chiar deasupra ta, la o altitudine de 90°. În contrast, la ecuator (latitudine 0°) Polaris ne-ar apărea la orizont, la o altitudine de 0°. Astfel că altitudinea Polaris este practic egală cu latitudinea ta: dacă ai fi la Paris, la o latitudine de aproximativ 49° N, ai măsura altitudinea lui Polaris la aproximativ 49°.

Latitudinea = altitudinea Stelei Polare                                    (Ecuaţia 4)

Navigatorii de pe vremuri foloseau un astrolab marinăresc, şi navigau ghidaţi de stele, oarecum asemănător ghidajului după Soare. Şi de data aceasta noi vom folosi smartphone-ul.

Materiale

• Un smartphone având instalate aplicaţiile înclinometru şi planetarium
• Binoclu (opţional)
• Lanternă (opţional)

Procedura

Este mai simplu de calculat latitudinea locală folosind Steaua Polară decât pe baza Soarelui: nu mai este necesar să se ia în calcul declinaţia, deoarece poziţia lui Polaris rămâne aceeaşi pe toată durata anului.

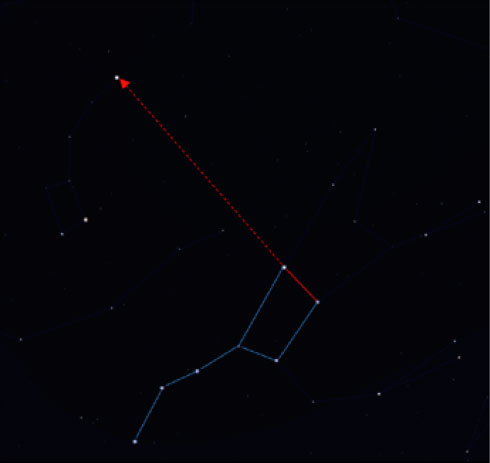
Cum găsiţi Steaua Polară? Căutaţi constelaţia Ursa Mare, cunoscută şi sub numele de Carul Mare sau Plugul (figura 9). Extindeţi o linie imaginară în sus de la cele mai depărtate două stele ale tetragonului, şi prelungiţi extinderea de vreo şapte ori cât distanţa dintre cele două stele. Prima stea strălucitoare pe acea linie este Polaris, care este parte a Ursei Mici, Carul Mic. Alternativ, puteţi folosi aplicaţia planetarium şi funcţia de căutare.

Deoarece este mai puţin strălucitoare decât Soarele, observările lui Polaris pot fi făcute în mod direct, fără alidadă, însă slaba sa strălucire o face destul de dificil de localizat. Poate ar fi util ca mai întâi să vă exersaţi abilitățile de măsurare prin practicarea pe obiecte luminoase, cum ar fi planetele sau Luna.

Cereţi elevilor următoarele:

1. Să-şi orienteze smartphone-urile cu muchia lungă în sus şi să puncteze cu ea direct către Steaua Polară, în timp ce privesc ecranul telefonului.

Va fi nevoie de un pic de lumină ambientală cât pentru a vedea muchia telefonului pe întuneric.

2. Să folosească aplicaţia înclinometru pentru a citi unghiul de elevaţie al Stelei Polare. Această valoare va constitui direct estimarea latitudinii locale.

Alternativ, lucrând în perechi, elevii pot folosi binoclul. Un elev va privi prin binoclu spre Polaris astfel încât steaua să fie în centrul câmpului vizual (sprijinind eventual binoclul de un suport, de un zid, spre exemplu, pentru a-l putea menţine nemişcat). Celălalt elev va aşeza smartphone-ul pe bunoclu şi va determina unghiul de elevaţie folosind aplicaţia înclinometru. Dacă este necesar (când binoclul nu are forme strict cilindrice) se va face o calibrare unghiulară a binoclului: se aşează binoclul pe o suprafaţă orizontală, se plasează smartphone-ul pe binoclu şi se citeşte unghiul determinat de aplicaţia înclinometru.

Discuţii

Cereți elevilor să caute altitudinea lui Polaris în aplicația planetarium. Cât de exactă a fost măsurătoarea lor? Cum se compară latitudinea estimată de ei cu latitudinea exactă dată de aplicația planetarium sau de funcția GPS de pe smartphone? La ce surse de eroare se pot gândi ei, în plus față de cele discutate în activitatea anterioară?

Deşi Polaris este o stea strălucitoare, ea este pentru noi mult mai palidă decât Soarele, ceea ce face mai greu de obţinut o determinare precisă a altitudinii ei.

O altă sursă de eroare este poziţia Stelei Polare. Spunem că Polaris ne-ar apărea chiar desupra (la zenit) dacă am fi la Polul Nord: deci la o elevaţie de 90°. În realitate, elevaţia ei este de 89,3°, ceea ce introduce o eroare de 0,7° în calculele elevilor, corespunzând unei erori liniare de 100 km.

Această metodă funcţionează cel mai bine la latitudini medii. Dacă ne apropiem de nord, este dificil de privit spre stea deoarece ea se află deasupra capului. Lângă ecuator, Polaris apare apropiată de orizont, ceea ce înseamnă că intervin abateri optice datorate atmosferei.

Recunoaşteri

Articolul de faţă se bazează pe o activitate publicată de ‘Ştiinţa pe scenă’, reţeaua europeană a profesorilor de ştiinţe, tehnologie, inginerie şi matematici (STEM), care a fost lansată în 1999 de EIROforum, editorul revistei Science in School. ‘Ştiinţa pe scenă’ adună profesori de ştiinţe din toată Europa, pentru a le facilita schimburile de idei şi pentru a permite asimilarea celor mai bune practici educaţionale.

La atelierele ‘Ştiinţa pe scenă’ din Vienna, Austria, şi din Berlin, Germania, precum şi prin dialogurile derulate prin email şi prin platforma de educaţie open-source Moodle, 20 de profesori din 14 ţări europene au colaborat pentru a realiza 11 unităţi de predare care arată cum smartphone-ul şi app-urile sale pot fi folosite în lecţii de matematică, fizică, chimie şi biologie. Aceste unităţi au fost publicate în 2014 prin ‘Ştiinţa pe scenă’ Germania sub numele iStage 2: Smartphones in Science Teaching^w4. Proiectul a fost sponsorizat de SAP.

Pe lângă Gerhard Rath şi Philippe Jeanjacquot, la realizarea acestui proiect s-au implicat intens şi Pere Compte din Spain şi Immacolata Ercolino din Italia. Martin Pratl a furnizat un ajutor substanţial la redactarea acestui text.