Έξυπνες μετρήσεις των ουρανών Teach article

Μετάφραση από την Αιμιλία Ξανθοπούλου. Βάλτε τους μαθητές σας να χρησιμοποιήσουν τα έξυπνα κινητά τηλέφωνα τους για λίγη πρακτική αστρονομία.

Που ακριβώς βρίσκεστε αυτή την στιγμή; Ένας τρόπος για να το βρείτε είναι να χρησιμοποιήσετε την δορυφορική λειτουργία προσδιορισμού θέσης (γνωστή και ως GPS) του κινητού σας τηλεφώνου. Στο παρελθόν, όμως, θα βασιζόσασταν στα αστέρια για να σας πουν που βρίσκεστε – ειδικά αν ήσασταν ναυτικός στην θάλασσα σε ένα τοπίο που σε μεγάλο βαθμό δεν είχε ιδιαίτερα χαρακτηριστικά.

Σε αυτό το άρθρο, περιγράφουμε μερικές από τις πρώτες εξελίξεις στην πλοήγηση που βασίζονται στα αστέρια, και δείχνουμε πως αυτές οι παραδοσιακές τεχνικές μπορούν να αναπαραχθούν στην τάξη χρησιμοποιώντας απλές εφαρμογές στο κινητό τηλέφωνο. Οι μαθητές σας μπορούν να χρησιμοποιήσουν τότε την λειτουργία του  GPS στα κινητά τους για να ελέγξουν την ακρίβεια της εργασίας τους πριν να λάβουν υπόψη τους τις πιθανές πηγές λάθους.

Κατάλληλες για μαθητές ηλικίας 14–18, οι δύο δραστηριότητες συνδέουν την ιστορία, την αστρονομία, την γεωγραφία και τα μαθηματικά: προσδιορισμός του γεωγραφικού σας πλάτους (εικόνα 1) χρησιμοποιώντας τον Ήλιο, και προσδιορισμός του γεωγραφικού σας πλάτους χρησιμοποιώντας τον Πολικό αστέρα. Από το τμήμα με το πρόσθετο υλικό μπορείτε να κατεβάσετε τις λεπτομέρειες για μια δραστηριότητα συνεργασίας μεταξύ των σχολείων, για τον υπολογισμό της περιφέρειας της Γης. Οι τρεις δραστηριότητες απαιτούν κάτι λίγο περισσότερο από ένα έξυπνο κινητό και δεν διαρκούν περισσότερο από μια ώρα η κάθε μια.

Προσδιορισμός του γεωγραφικού σας πλάτους χρησιμοποιώντας το ύψος του Ήλιου

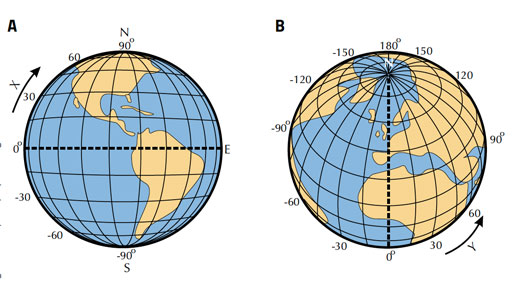
‘Τι είναι το μεσημέρι;’ μπορεί να φαίνεται σαν μια παράξενη ερώτηση. Σίγουρα το μεσημέρι είναι 12 η ώρα το μεσημέρι; Αν και ακριβολογώντας, ηλιακό μεσημέρι η ηλιακή μεσημβρία είναι η στιγμή που ο Ήλιος διασχίζει τον μεσημβρινό, η την γραμμή του γεωγραφικού μήκους, και συνήθως εμφανίζεται είτε βόρεια είτε νότια. Αυτό συμβαίνει όταν ο Ήλιος βρίσκεται στο υψηλότερο σημείο του στον ουρανό και οι σκιές είναι στο μικρότερο μήκος τους. Είναι η στιγμή που η θέση του Ήλιου μπορεί να χρησιμοποιηθεί για να προσδιορίσετε το γεωγραφικό σας πλάτος, η την γωνιακή απόσταση από τον ισημερινό.

Πως γίνεται αυτό; Ας θεωρήσουμε την περίπτωση σε μια από τις ισημερίες (περίπου στις 20 Μαρτίου και 23 Σεπτεμβρίου κάθε χρόνου), όταν το επίπεδο του ισημερινού περνά από το κέντρου του Ήλιου (εικόνα 2).

• Α: Φανταστείτε ότι στέκεστε στον ισημερινό, γεωγραφικό πλάτος 0°, το μεσημέρι: ο Ήλιος είναι ακριβώς πάνω από το κεφάλι σας. Αν μετρούσατε το ύψος του Ήλιου (την γωνία ανύψωσης πάνω από τον ορίζοντα), θα το βρίσκατε 90° (εικόνα 3A). Αφαιρώντας αυτό το νούμερο από τις 90° βρίσκετε 0°, που είναι το  γεωγραφικό σας πλάτος.

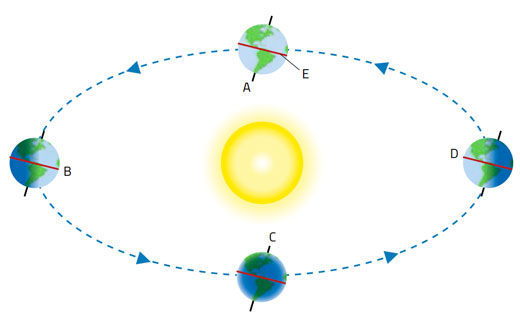
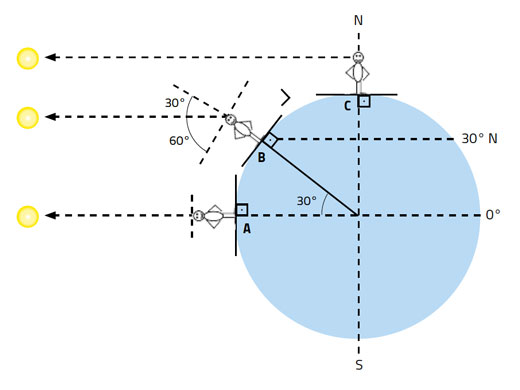
(Δηλώσαμε ότι το μεσημέρι, ο Ήλιος είναι συνήθως είτε βόρεια είτε νότια. Στις ισημερίες, είναι ακριβώς πάνω από το κεφάλι μας.)

• Β: Μια φίλη σας στέκεται στο Βόρειο η στον Νότιο Πόλο (γεωγραφικά πλάτη 90° Β η 90° Ν, αντίστοιχα). Την ίδια στιγμή, θα έβλεπε τον Ήλιο να βρίσκεται ακριβώς στον ορίζοντα: σε ένα ύψος 0° (εικόνα 3B). Αφαιρώντας αυτό το νούμερο από τις 90° βρίσκετε 90°, που είναι το γεωγραφικό της πλάτος.
• C: Ένας άλλος φίλος είναι στον ίδιο μεσημβρινό όπως και εσείς, αλλά σε γεωγραφικό πλάτος 30° Β. Επειδή βρίσκεται στον ίδιο μεσημβρινό, είναι επίσης και για αυτόν μεσημέρι, αλλά παρατηρεί τον Ήλιο σε ένα ύψος 60° πάνω από τον ορίζοντα (εικόνα 3C).  Αφαιρώντας αυτό το νούμερο από τις  90° βρίσκετε 30°: το γεωγραφικό του πλάτος.

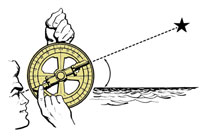
Γεωγραφικό πλάτος = 90° – ύψος του Ήλιου το μεσημέρι στην ισημερία    (Εξίσωση 1)

Πως μπορούμε να χρησιμοποιήσουμε πρακτικά αυτή την γνώση; Στον 15ο και στις αρχές του 16ου αιώνα, πολλοί θαλασσοπόροι χρησιμοποιούσαν τους ναυτικούς αστρολάβους για να μετρήσουν το ύψος του Ήλιου και επομένως να υπολογίσουν το γεωγραφικό πλάτος του πλοίου τους. Ο ναυτικός αστρολάβος ήταν ουσιαστικά ένα κλισιόμετρο: αιωρούμενο στο κατακόρυφο επίπεδο, στρεφόταν προς ένα ουράνιο σώμα, για παράδειγμα τον Ήλιο. Ένα περιστρεφόμενο κλισιόμετρο χρησιμοποιούνταν για να διαβάσει το ύψος του ουράνιου σώματος από την κλίμακα γύρω από τον εξωτερικό δακτύλιο (εικόνα 4).

Ενώ είναι σχετικά εύκολο να κατασκευαστεί^w2  ένας ναυτικός αστρολάβος, είναι επίσης το ίδιο εύκολο να χρησιμοποιήσετε ένα έξυπνο κινητό τηλέφωνο για να μετρήσετε το ύψος του Ήλιου με την βοήθεια μια εφαρμογής κλισιομέτρου. Πριν, όμως, το κάνουμε αυτό, πρέπει να παρουσιάσουμε μια μικροβελτίωση έτσι ώστε οι υπολογισμοί μας να ισχύουν για όλο τον χρόνο.

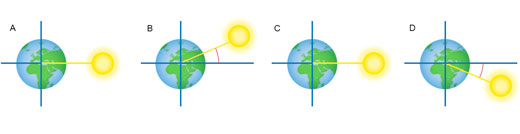
Εξαιτίας της κλίσης του άξονα περιστροφής της Γης (23.45°) και του γεγονότος ότι η Γη περιφέρεται γύρω από τον Ήλιο, μόνο στις ισημερίες ο Ήλιος εμφανίζεται ακριβώς πάνω από τον ισημερινό. Ξεκινώντας από την ισημερία του Μαρτίου, η θέση του Ήλιου το μεσημέρι εμφανίζεται να κινείται βόρεια του ισημερινού, φτάνοντας στην μέγιστη γωνία των +23.45° στο ηλιοστάσιο του Ιουνίου, γυρίζοντας στις 0° στην ισημερία του Σεπτεμβρίου, και κινούμενη νότια του ισημερινού για να φτάσει στις -23.45° στο ηλιοστάσιο του Δεκεμβρίου. Αυτή η γωνία είναι γνωστή ως απόκλιση του Ήλιου (εικόνα 5).

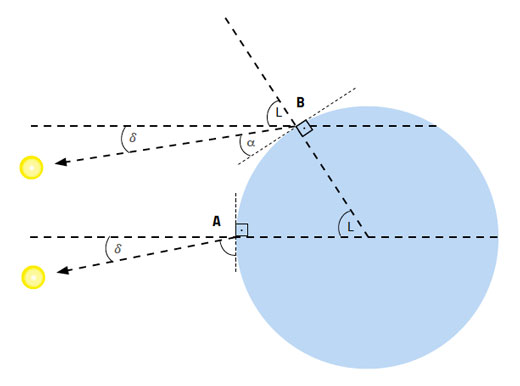
Έτσι το ύψος του Ήλιου το μεσημέρι, το οποίο οι πρώτοι θαλασσοπόροι μετρούσαν με τον ναυτικό αστρολάβο και το οποίο εμείς μπορούμε να μετρήσουμε με ένα έξυπνο κινητό τηλέφωνο, εξαρτάται και από την εποχή του χρόνου – και επομένως την απόκλιση του Ήλιου – και από το γεωγραφικό μας πλάτος (εικόνα 6):

Ύψος του Ήλιου το μεσημέρι = 90° + απόκλιση – γεωγραφικό πλάτος   (Εξίσωση 2)

Η, με ανακατάταξη:

Γεωγραφικό πλάτος = 90° – ύψος του Ήλιου το μεσημέρι + απόκλιση  (Εξίσωση 3)

Για να καθορίσουν την απόκλιση του Ήλιου, οι πρώτοι θαλασσοπόροι χρησιμοποιούσαν πίνακες δεδομένων η εξελιγμένους ναυτικούς αστρολάβους με την απόκλιση του Ήλιου σημειωμένη στον περιστρεφόμενο δίσκο. Μπορούμε να βρούμε τις ίδιες πληροφορίες από την εφαρμογή του πλανητάριου, και μετά να υπολογίσουμε την ανύψωση του Ήλιου και να καθορίσουμε το γεωγραφικό μας πλάτος.

Υλικά

Κάθε ομάδα μαθητών θα χρειαστεί:

• Ένα έξυπνο κινητό τηλέφωνο με εγκαταστημένες μια εφαρμογή κλισιομέτρου και μια εφαρμογή πλανητάριου
• Καλαμάκι
• Κολλητική ταινία
• Αλφάδι (προαιρετικό)

Διαδικασία

Για να προσδιορίσουν το γεωγραφικό τους πλάτος, οι μαθητές σας θα χρειαστεί:

1. Να χρησιμοποιήσουν κολλητική ταινία για να στερεώσουν το καλαμάκι κατά μήκος της μιας πλευράς του κινητού (εικόνα 7). Αυτό είναι το κλισιόμετρο.
2. Να χρησιμοποιήσουν την εφαρμογή του πλανητάριου για να προσδιορίσουν την τοπική ώρα του ηλιακού μεσημεριού και την απόκλιση του Ήλιου. 

Ανάλογα με την  τοποθεσία σας μέσα στην ζώνη ώρας σας, το ηλιακό μεσημέρι μπορεί να είναι τόσο νωρίς όπως 11:30 το πρωί, και εξαιτίας της θερινής ώρας, θα μπορούσε να είναι τόσο αργά όπως 1.30 μετά το μεσημέρι.

3. Κρατώντας το κινητό με το καλαμάκι στο άνω άκρο, στρέψτε το καλαμάκι προς τον Ήλιο. Όταν η σκιά από το καλαμάκι έχει το μικρότερο μήκος, το κινητό είναι σωστά ευθυγραμμισμένο (εικόνα 7).
4. Χρησιμοποιώντας την εφαρμογή του κλισιομέτρου, διαβάστε την γωνία ανύψωσης του Ήλιου.
5. Χρησιμοποιήστε την εξίσωση 2 για να υπολογίσετε το γεωγραφικό πλάτος.

Διαφορετικά, για να δώσετε στους μαθητές την δυνατότητα να στοχεύσουν με τα κινητά τους με μεγαλύτερη ακρίβεια τον Ήλιο και επομένως να μετρήσουν με μεγαλύτερη ακρίβεια την ανύψωση του Ήλιου, θα μπορούσαν να κατασκευάσουν ένα υποστήριγμα που θα μπορούσε να τοποθετηθεί σε ένα τρίποδο. Πλήρεις πληροφορίες για τα υλικά και την κατασκευή διατίθενται στο διαδίκτυο^w3.

Συζήτηση

Ζητήστε από τους μαθητές σας να συγκρίνουν τα αποτελέσματα τους με το ακριβές γεωγραφικό πλάτος όπως δίνεται από την λειτουργία του GPS στο κινητό τους η χρησιμοποιώντας την εφαρμογή του πλανητάριου. Πόσο ακριβής ήταν η δικιά τους υπολογιζόμενη τιμή; Ποιες πηγές σφάλματος θα μπορούσαν να υπάρχουν;

Φυσικά, η ακρίβεια εξαρτάται από την ακρίβεια της εργασίας των μαθητών, π.χ. με πόση ακρίβεια ήταν ευθυγραμμισμένο το καλαμάκι με την άκρη του τηλεφώνου η αν η σκιά ήταν πραγματικά η μικρότερη. Για μέγιστη ακρίβεια, οι μετρήσεις θα πρέπει να γίνονται το μεσημέρι, αλλά μερικά λεπτά πριν η μετά δεν θα επηρέαζαν πολύ τον υπολογισμό γιατί όταν ο Ήλιος βρίσκεται στο υψηλότερο σημείο του, η αλλαγή στο ύψος του είναι πιο αργή.

Τα έξυπνα τηλέφωνα μπορούν να μετρήσουν γωνίες κλίσης με ακρίβεια 0.1°, που δεν είναι κακή. Παρόλα αυτά θα ήταν ενδιαφέρον να καλιμπράρετε (βαθμονομήσετε) την εφαρμογή του κλισιομέτρου με ένα αλφάδι για να δείτε αν η ανάγνωση των 0.0° είναι πράγματι οριζόντια.

Θα μπορούσατε επίσης να ρωτήσετε τους μαθητές σας γιατί νομίζουν ότι παρόλο που το γεωγραφικό πλάτος μπορούσε να προσδιοριστεί στον αρχαίο κόσμο, μόλις μόνο τον 18ο αιώνα υπήρξε η δυνατότητα να μετρηθεί το γεωγραφικό μήκος.

Η απάντηση βρίσκεται στην περιστροφή της Γης: 360° σε μια μέρα η περίπου 15° κάθε ώρα. Έτσι συγκρίνοντας την τοπική ώρα με την ώρα σε ένα σημείο αναφοράς με γνωστό γεωγραφικό μήκος, είναι δυνατόν να προσδιορίσετε το γεωγραφικό σας μήκος. Η τοπική ώρα μπορούσε να υπολογιστεί από τον Ήλιο, αλλά η δυσκολία ήταν ο χρόνος στο σημείο αναφοράς: ένα ρολόι που να δείχνει τον χρόνο με ακρίβεια, ακόμη πάνω και σε ένα κινούμενο πλοίο, εφευρέθηκε μόλις το 1759, από τον John Harrison.

Προσδιορισμός του γεωγραφικού σας πλάτους χρησιμοποιώντας το ύψος του Πολικού Αστέρα

Στην προηγούμενη δραστηριότητα, μετρήσαμε το ύψος του Ήλιου στο τοπικό μεσημέρι: καθώς ο Ήλιος διασχίζει τον μεσημβρινό σας. Είναι σε αυτή την στιγμή – και μόνο σε αυτή την στιγμή – που ο Ήλιος θα εμφανιστεί η στον νότο η στον βορρά. Αν οι μαθητές σας υπολόγιζαν το γεωγραφικό τους πλάτος από τον Ήλιο σε άλλες στιγμές της μέρας, τα αποτελέσματα τους θα ήταν τρομερά ανακριβή. Ευτυχώς, υπάρχει μια άλλη μέθοδος που δεν εξαρτάται τόσο σημαντικά από τον χρόνο – μολονότι λειτουργεί μόνο στο βόρειο ημισφαίριο και πρέπει να γίνει αφού νυχτώσει – βασιζόμενη στον Πολικό Αστέρα, το Αστέρι του Βορρά.

Ενώ οι θέσεις των άλλων αστεριών φαίνεται να αλλάζουν κατά την διάρκεια της νύχτας, ο Πολικός Αστέρας εμφανίζεται να παραμένει σταθερός στον βορρά (εικόνα 8), επειδή η θέση του βρίσκεται στην γραμμή του άξονα περιστροφής της Γης. Αν στεκόσασταν στον Βόρειο Πόλο (γεωγραφικό πλάτος 90° Β), ο Πολικός Αστέρας θα φαινόταν ακριβώς πάνω από το κεφάλι σας, σε ένα ύψος 90°. Σε αντίθεση, στον ισημερινό (γεωγραφικό πλάτος 0°), ο Πολικός Αστέρας θα φαινόταν στον ορίζοντα, σε ύψος 0°. Έτσι το ύψος του Πολικού Αστέρα είναι ίσο με το γεωγραφικό του πλάτος: αν ήσασταν στο Παρίσι, σε γεωγραφικό πλάτος περίπου 49° Β, θα μετρούσατε το ύψος του Πολικού Αστέρα ως περίπου 49°.

Γεωγραφικό πλάτος = ύψος του Πολικού Αστέρα  (Εξίσωση 4)

Οι πρώτοι θαλασσοπόροι χρησιμοποιούσαν τον ναυτικό αστρολάβο για να βρίσκουν το δρόμο με την βοήθεια των αστεριών, όπως το έκαναν και για να βρίσκουν τη πορεία τους χρησιμοποιώντας τον Ήλιο. Πάλι μπορούμε να χρησιμοποιήσουμε ένα κινητό.

Υλικά

• Έξυπνο κινητό τηλέφωνο με εγκατεστημένες τις εφαρμογές του κλισιομέτρου και του πλανητάριου
• Κυάλια (προαιρετικά)
• Φακός (προαιρετικός)

Διαδικασία

Είναι πιο απλό να υπολογίσετε το γεωγραφικό σας πλάτος από τον Πολικό Αστέρα παρά από τον Ήλιο: δεν είναι απαραίτητο να λάβετε υπόψη την απόκλιση, γιατί η θέση του Πολικού Αστέρα παραμένει αμετάβλητη όλο τον χρόνο.

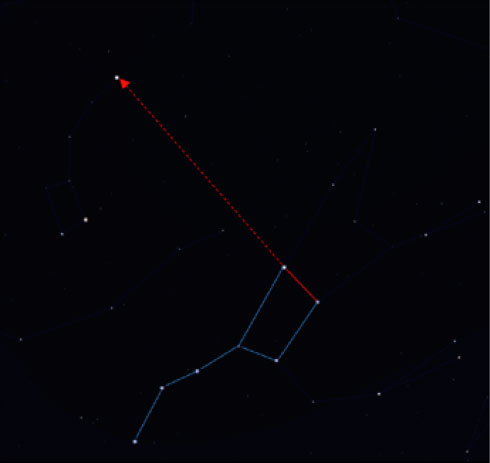
Πως μπορείτε να βρείτε τον Πολικό Αστέρα; Ψάξτε για τον αστερισμό Ursa Major, γνωστό επίσης και ως Μεγάλη Άρκτο η Plough (Άροτρο) (εικόνα 9). Προεκτείνετε μια φανταστική γραμμή προς τα πάνω από τα δύο πιο μακρινά αστέρια του τετραγώνου, επεκτείνοντας περίπου επτά φορές την μεταξύ τους απόσταση. Το πρώτο φωτεινό αστέρι κατά μήκος αυτής της γραμμής είναι ο Πολικός Αστέρας, που είναι μέρος του αστερισμού Ursa Minor, της Μικρής Άρκτου. Εναλλακτικά μπορείτε να χρησιμοποιήσετε την εφαρμογή του πλανητάριου και την λειτουργία αναζήτησης.

Επειδή είναι πιο αμυδρός από τον Ήλιο, οι παρατηρήσεις του Πολικού Αστέρα μπορεί να γίνουν απευθείας, χωρίς το κλισιόμετρο, αλλά η αμυδρότητα του επίσης δυσκολεύει αρκετά τον  εντοπισμό του. Μπορεί να βοηθήσει αν εκπαιδεύσετε τις δεξιότητες σας στην μέτρηση κάνοντας εξάσκηση σε πιο φωτεινά αντικείμενα όπως τους πλανήτες η τη Σελήνη.

Ζητήστε από τους μαθητές σας να:

1. Κρατήσουν τα κινητά τους με την μεγαλύτερη πλευρά προς τα πάνω, και μετά να τα στρέψουν κατευθείαν προς τον Πολικό Αστέρα, κοιτάζοντας κατά μήκος της μπροστινής πλευράς του τηλεφώνου.

Θα χρειαστούν λίγο περιβάλλον φυσικό φως για αυτό, για να αναγνωρίσουν την άκρη του τηλεφώνου στο σκοτάδι.

2. Χρησιμοποιώντας την εφαρμογή του κλισιομέτρου, διαβάστε την γωνία ανύψωσης του Πολικού Αστέρα. Αυτή είναι η εκτίμηση του γεωγραφικού σας πλάτους.

Διαφορετικά, δουλεύοντας σε ζευγάρια, θα μπορούσαν να χρησιμοποιήσουν τα κυάλια. Ο ένας μαθητής θα πρέπει να στρέψει τα κυάλια προς τον Πολικό Αστέρα έτσι ώστε το αστέρι να είναι στο κέντρο του οπτικού πεδίου (ακουμπήστε τα κυάλια σε, παραδείγματος χάριν, έναν τοίχο για να τα κρατήσετε σταθερά). Ένας άλλος μαθητής θα πρέπει να ακουμπήσει το κινητό τηλέφωνο πάνω στα κυάλια και να προσδιορίσει την γωνία ανύψωσης χρησιμοποιώντας την εφαρμογή του κλισιομέτρου. Αν είναι απαραίτητο, καλιμπράρετε τα κυάλια: τοποθετήστε τα πάνω σε μια οριζόντια επιφάνεια, βάλτε το κινητό τηλέφωνο από πάνω τους και ελέγξτε την γωνία στην εφαρμογή του κλισιομέτρου.

Συζήτηση

Ζητήστε από τους μαθητές σας να ψάξουν το ύψος του Πολικού Αστέρα στην εφαρμογή του πλανητάριου. Πόσο ακριβείς ήταν οι μετρήσεις τους; Πως συγκρίνεται το εκτιμώμενο γεωγραφικό τους πλάτος με το ακριβές γεωγραφικό πλάτος που δίνεται από την εφαρμογή του πλανητάριου η την λειτουργία GPS στο κινητό; Ποιες πηγές σφάλματος θα μπορούσαν να σκεφτούν, εκτός από αυτές που συζητήθηκαν στην προηγούμενη δραστηριότητα;

Παρόλο που ο Πολικός Αστέρας είναι ένα φωτεινό αστέρι, είναι πολύ πιο αμυδρός από τον Ήλιο, και αυτό δυσκολεύει μια ακριβή ανάγνωση του ύψους του.

Μια άλλη πηγή λάθους είναι η θέση του Πολικού Αστέρα. Είπαμε ότι ο Πολικός Αστέρας θα εμφανιζόταν ακριβώς πάνω από το κεφάλι σας αν στεκόσασταν στον Βόρειο Πόλο: σε ένα ύψος 90°. Στην πραγματικότητα, το ύψος του θα ήταν 89.3°,  που εισάγει ένα σφάλμα 0.7° στους υπολογισμούς των μαθητών σας, που αντιστοιχεί σε περίπου 100 χιλιόμετρα.

Αυτή η μέθοδος λειτουργεί καλύτερα σε μεσαία γεωγραφικά πλάτη. Πολύ πιο βόρεια, είναι δύσκολο να στοχεύσετε σε ένα αστέρι, που εμφανίζεται ακριβώς πάνω από το κεφάλι σας. Κοντά στον ισημερινό, ο Πολικός Αστέρας εμφανίζεται κοντά στον ορίζοντα, που σημαίνει ότι υπάρχουν διαταραχές που εισάγονται από την ατμόσφαιρα.

Ευχαριστίες

Αυτό το άρθρο είναι βασισμένο σε μια δραστηριότητα που δημοσιεύτηκε από το Science on Stage, το δίκτυο των Ευρωπαίων εκπαιδευτικών φυσικών επιστημών, τεχνολογίας, μηχανικής και μαθηματικών (STEM), που ξεκίνησε το 1999 από το EIROforum, τον εκδότη του Science in School. Το Science on Stage φέρνει σε επαφή εκπαιδευτικούς φυσικών επιστημών από όλη την Ευρώπη με σκοπό να ανταλλάξουν ιδέες διδασκαλίας και την καλύτερη πρακτική με ενθουσιώδεις συναδέλφους από 25 χώρες.

Σε σεμινάρια του Science on Stage στην Βιέννη, Αυστρία, και Βερολίνο, Γερμανία, καθώς επίσης και σε συζητήσεις μέσω ηλεκτρονικού ταχυδρομείου (email) και την ανοιχτού κώδικα πλατφόρμα μάθησης Moodle, 20 εκπαιδευτικοί από 14 Ευρωπαϊκές χώρες συνεργάστηκαν για να αναπτύξουν 11 διδακτικές ενότητες που δείχνουν πως τα κινητά τηλέφωνα και οι εφαρμογές τους μπορούν να χρησιμοποιηθούν στα μαθήματα των μαθηματικών, της φυσικής, της χημείας η της βιολογίας. Αυτές οι ενότητες δημοσιεύτηκαν το 2014 από το Science on Stage Γερμανία ως iStage 2: Έξυπνα κινητά τηλέφωνα στην Διδακτική των Φυσικών Επιστημών^w4. Το πρόγραμμα συντηρείται από το SAP.

Εκτός από τον Gerhard Rath και τον Philippe Jeanjacquot, ο Pere Compte από την Ισπανία και η Immacolata Ercolino από την Ιταλία είχαν μεγάλη συμμετοχή στην ανάπτυξη αυτού του προγράμματος. Ο Martin Pratl παρείχε πολύτιμη βοήθεια στο κείμενο του άρθρου.