Paralaxe: chegando às estrelas com geometria Teach article
Traduzido por Pedro Augusto. Quão longe estão as estrelas? Explore na sua sala de aula como medem os astrónomos as distâncias no espaço.

Gaia, com a Via Láctea de
fundo
A imagem é cortesia da ESA /
ATG medialab; imagem de
fundo: ESO / S Brunier
Olhe para fora da janela de um carro ou de um comboio em movimento e notará que a sua visão dos objetos se altera com a respetiva distância: os arbustos ou árvores próximos parecem passar a voar, enquanto uma árvore ou um edifício mais distante parecem deslocar-se muito mais devagar.
Esta aparente alteração da posição que depende da distância é chamada de paralaxe. Pode reproduzir o efeito fazendo um sinal com o polegar para cima em frente à sua cara e observando o polegar em primeiro lugar com o olho esquerdo (apenas) e depois apenas com o olho direito. Conforme altera os olhos, o seu polegar parece saltar de lado em relação às imagens de fundo – porque os seus dois olhos estão em posições ligeiramente diferentes. Agora estique o seu braço tão longe quanto este pode ir e, deslocando o polegar para mais próximo da sua cara, repita a experiência anterior: notará que a deslocação em posição aparente aumenta quando a distância entre o seu polegar e os seus olhos diminui.
Este efeito é já usado há séculos para a determinação de distâncias no espaçow1. Em meados do século XIX, os astrónomos usaram a paralaxe para determinar as primeiras distâncias estelares. Os topógrafos também usam esta forma de medição para desenharem mapas detalhados da superfície da Terra. Presentemente, o satélite Gaia da ESA, lançado em dezembro de 2013, está a medir paralaxes precisas para mais de um bilião de estrelas na nossa galáxia, a Via Láctea, aumentando a precisão de um fator de cerca de 200.
Neste artigo, descrevemos uma atividade que explora a forma como os astrónomos usam a paralaxe para medir distâncias interestelares, determinando a distância a uma ‘estrela’ colocada na sala de aula. Existe, ainda, um curto artigo na web sobre a história de medições de paralaxe, que pode descarregar da secção de material adicionalw1.
A atividade aqui descrita reproduz a geometria básica das medições de paralaxe, usando aparelhos simples para a medição de ângulos. Utilizámos esta atividade com sucesso, que leva de 30 a 45 minutos incluindo montagem, com estudantes de idades entre 13 e 17 anos. No próximo número do Science in School, vamos descrever um método fotográfico para efetivar medições de paralaxe que é ainda mais preciso e astronomicamente realista.
Atividade: a geometria da paralaxe
Para esta atividade, vai precisar de um instrumento para medir ângulos entre linhas-de-visão – um teodolito (ver figura 1), se existir um entre o equipamento de Matemática, Física ou Geografia da escola. Caso contrário, damos aqui instruções em como construir um aparelho de medições de ângulos semelhante, a partir de materiais facilmente disponíveis.

A imagem é cortesia de HdA / M Pössel
Material
- Dois teodolitos
- Pequena esfera ou LED como ‘estrela’
- Fita métrica
Se não tiver acesso a teodolitos pode improvisar construindo os aparelhos simples apresentados na figura 2. Para cada um (serão precisos dois) vai precisar de:
- Folha de papel
- Cartolina com cerca de 4 cm x 8 cm
- Pequeno bloco de madeira, com cerca de 1 cm x 3 cm x 8 cm
- Mesa ou outra superfície horizontal

A imagem é cortesia de HdA / M Pössel
Procedimento
A montagem básica pode ser vista na figura 3. Para simplificar, fazemos todas as medições angulares no plano definido pelos pontos A, B e C, que deve ser paralelo ao chão.

A imagem é cortesia de HdA / M Pössel
Montagem
- Dividir a sala em duas partes marcando uma linha no chão, como indicado pela linha a tracejado. A parte do lado direito da sala com os dois teodolitos (ou, em alternativa, com os dois aparelhos improvisados) representa a Terra, enquanto a parte do lado esquerdo da sala representa o espaço.
- Coloque a ‘estrela’ na região do espaço (posição A na figura 3). Para a estrela pode usar um LED, um ornamento de Natal, uma bola de ping-pong ou outra pequena esfera. Coloque a estrela como conseguir – recorrendo a um tripé, num cabo de vassoura, num porta-guarda-chuva ou pendurada do teto.
Siga os passos para a montagem que se seguem, se estiver a utilizar teodolitos:
- Monte os dois teodolitos, cada um no seu tripé, na região da Terra. Vai ser necessário ajustar a mesa de suporte de cada um, de forma a esta ficar completamente horizontal (use um nível de bolha, se existir).
- Ajuste o ângulo de declinação (lido na escala semicircular branca da figura 1) para zero. Isto mantém as linhas-de-visão (através das miras da figura 1) no plano horizontal, onde vamos fazer todas as medições de ângulos e comprimentos.
- Ajuste a altura do teodolito à da estrela. Pode fazer isto elevando as pernas telescópicas em tripé do teodolito. Com a estrela a alguma distância do teodolito, observe através das miras e ajuste o tripé até que a estrela fique diretamente numa linha-de-visão. Provavelmente terá de voltar a ajustar a mesa rotativa de forma a garantir que ainda se mantém horizontal.
Alternativamente, se não estiver a usar teodolitos, siga os seguintes passos para contruir os aparelhos improvisados:
- Cole uma folha de papel em cada uma das mesas ou superfícies planas de observação de forma a criar duas plataformas de observação correspondentes às posições do teodolito B e C da figura 3.
- Faça a mira (a reta por onde se olha) colando rigidamente o pedaço de cartão ao bordo do bloco de madeira, como mostrado na figura 2.
- Ajuste a altura da sua estrela (posição A na figura 3) de forma a estar, exatamente, à mesma altura acima do solo das duas miras. Depois, de cada uma das suas duas posições, deve ser capaz de ajustar a posição das miras de tal forma a poder olhar ao longo do cartão, exatamente de lado, em linha reta até à estrela.
Fazendo as medições
A sua tarefa agora é determinar a distância entre o seu ponto de observação e a estrela, fazendo todas as suas medições apenas na Terra. É claro que não pode simplesmente usar a fita métrica e esticá-la de B a A, uma vez que isso significaria deixar a Terra. Nós não conseguimos medir as distâncias a objetos astronómicos fora do nosso Sistema Solar voando até lá.
Em vez disso, vamos medir dois ângulos e o comprimento de um lado do triângulo ABC e a geometria vai-nos ajudar a descobrir o comprimento dos outros dois lados, AB e AC. Com o teodolito na posição B, podemos medir o ângulo ABC como segue:
- Aponte a mira do teodolito B na direção do teodolito C. Leia o ângulo de azimute do respetivo disco (a escala preta na mesa rotativa da figura 1). Isto funciona melhor se ambos os teodolitos estiverem apontados um para o outro ao mesmo tempo.
- Depois, aponte a mira do teodolito B na direção da estrela em A. Mais uma vez, leia o valor do ângulo de azimute.
- Subtraia um dos valores de azimute pelo outro. Isto dá o valor do ângulo ABC.
- Repita o procedimento com o teodolito na posição C, de modo a obter o ângulo ACB.
- Finalmente, meça a distância entre os pontos B e C ao longo da linha-de-base, usando fita métrica.
Com os aparelhos improvisados, as mesmas medições angulares podem ser feitas como segue, em primeiro para o aparelho em B:
- Desenhe um ponto na folha de papel. Este será a referência.
- Coloque a mira de forma à parte baixa do cartão tocar no ponto de referência e a parte superior (ao longo da qual está a olhar) apontar diretamente ao outro aparelho, colocado em C. (Isto funciona melhor se os dois aparelhos estiverem apontados um para o outro ao mesmo tempo, com as partes superiores dos cartões de mira alinhados um com o outro.)
- Marque a posição da mira traçando uma reta no papel (como se mostra na figura 2).
- Repita o procedimento, olhando agora com o aparelho B a estrela em A, mais uma vez visualizando através da parte superior do cartão enquanto a inferior toca no ponto de referência e traçando um reta ao longo da aresta inferior.
- Use um transferidor para medir o ângulo entre as duas retas que desenhou. Este é o ângulo ABC.
- Repita o procedimento, utilizando o aparelho em C, olhando para B e para A à vez e desenhando as linhas-de-visão. Estas vão dar o ângulo ACB.
- Finalmente, meça a distância entre os pontos B e C ao longo da linha-de-base utilizando a fita métrica.
Descobrindo a distância da estrela
Agora sabe os ângulos de visão da estrela de duas posições diferentes da Terra e ainda a distância entre estas posições. Assim, como utilizamos estes resultados para determinar a distância à estrela? Primeiro, repare na geometria da situação, mostrada na figura 4.
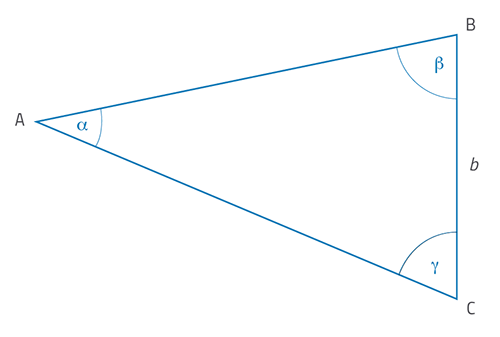
A imagem é cortesia de HdA / M Pössel
Nesta disposição a posição A da estrela e as posições B e C do teodolito estão todas no mesmo plano horizontal e formam o triângulo ABC (diretamente visto de cima). Os ângulos b e g são os valores medidos dos ângulos ABC e ACB, respetivamente, e o comprimento b é a distância medida ao longo da linha-de-base entre B e C.
Utilizando as suas próprias medições, desenhe um diagrama em escala de um triângulo como este tão preciso quanto possível: uma escala de 1:50 numa folha A3 dá bons resultados. Depois, pode simplesmente medir as distâncias AB e AC do diagrama e convertê-las em distâncias reais de forma a determinar as distâncias B e C para a estrela A.
De forma a verificar os seus resultados, infrinja as regras! Viaje pelo ‘espaço’ e use a fita métrica para medir AB e BC.
Finalmente, discuta a precisão dos resultados obtidos com a medição de ângulos. Se tivessemos usado distâncias maiores como se alteraria esta precisão? e porquê?

A imagem é cortesia da ESA / Gaia
Medições no espaço
Esperamos que os alunos gozem da sensação de descoberta a partir desta atividade e que fiquem com alguma ideia da forma como as medições de distâncias são feitas em Astronomiaw1. É claro que os procedimentos astronómicos reais utilizam métodos elaborados de forma a garantir a máxima precisão possível, já que as estrelas estão muito longe e os seus desvios de paralaxe são tão minúsculos. Mesmo o nosso mais próximo vizinho estelar fora do Sistema Solar (Proxima Centauri) está cerca de 100 000 vezes mais longe do que a mais longa distância que pode ser medida com uma linha-de-base a partir da Terra, isto é, duas vezes a distância entre a Terra e o Sol, se recolhermos imagens separadas de meio ano. Isto é como tentar detetar o desvio em paralaxe de um objeto a 100 quilómetros quando nos deslocamos um metro para o lado.
Web References
- w1 – Material de base sobre a história das medições de paralaxe pode ser descarregado da secção de materiais adicionais.
Resources
- Para uma fonte útil sobre a história da medição de paralaxes, ver:
- Hirshfeld AW (2013) Parallax: The Race to Measure the Cosmos. Mineola, NY, USA: Dover Publications. ISBN: 9780486490939
- Uma experiência de paralaxe utilizando um aparelho de medição de ângulos improvisado, como no artigo, está descrita aqui:
- Ferguson JL (1977) More parallax without pain. American Journal of Physics 45(12): 1221-1222. doi: 10.1119/1.10697
- Para informação sobre como fazer medições de paralaxe astronómica a sério com telescópios astronómicos, grandes e pequenos, ver:
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46. doi: 10.1088/0143-0807/30/1/004
- Cenadelli D et al. (2016) Geometry can take you to the Moon. Science in School 35: 41-46.
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11/2014: 72-77
- Ratcliff SJ et al. (1993) The measurement of astronomical parallaxes with CCD imaging cameras on small telescopes. American Journal of Physics 61(3): 208. doi: 10.1119/1.17292
Review
A paralaxe estelar é o mais velho, mais simples e mais preciso método para a determinação de distâncias às estrelas. Este artigo explica como fazer medições terrestres utilizando este método. Se seguir as instruções, vai conseguir medir a distância dentro da sala de aula a um objeto, a ‘estrela’, e os seus alunos vão entender como podem os astrónomos calcular as imensas distâncias do espaço.





