Paralaksa: gwiezdna geometria Teach article
Tłumaczenie Ewa Stokłosa. Jak bardzo oddalone są od nas gwiazdy? Poznajcie metody mierzenia odległości w kosmosie przez astronomów.

z Drogą Mleczną w tle
Zdjęcie dzięki uprzejmości ESA
/ ATG medialab; tło: ESO / S
Brunier
Spójrz przez okno poruszającego się samochodu czy pociągu, a zauważysz, że postrzeganie obiektów zależy od tego, w jakiej odległości od ciebie się one znajdują: pobliskie krzaki i drzewa wydają się pędzić, a bardziej oddalone budynki zdają się poruszać o wiele wolniej.
Pozorna zmiana w położeniu zależna od odległości to paralaksa. Można ją zrozumieć wyciągając przed siebie palec i spoglądając na niego najpierw tylko lewym okiem, a później prawym. Gdy spojrzysz na palec drugim okiem odniesiesz wrażenie, że przemieszcza się on względem obiektów tła – co jest wynikiem niewielkiej różnicy w położeniu oczu. Teraz wyciągnij rękę przed siebie i powtórz eksperyment z patrzeniem jednym okiem przysuwając palec do twarzy: zauważysz, że pozorna zmiana położenia palca jest tym większa, im mniejsza jest odległość między palcem i oczami.
Zjawisko to od wieków służy do obliczania odległości w kosmosiew1. W połowie XIX wieku astronomowie wykorzystali paralaksę do pierwszych pomiarów odległości do gwiazd. Pomaga ona również geodetom przy tworzeniu dokładnych map powierzchni Ziemi. Satelita Gaia należąca do Europejskiej Agencji Kosmicznej (ESA), która została wystrzelona w grudniu 2013 roku, w sposób nadzwyczaj precyzyjny mierzy obecnie paralaksy ponad miliarda gwiazd naszej galaktyki, Drogi Mlecznej. Jej pomiary są około 200 razy dokładniejsze niż wcześniejsze.
W artykule przedstawiamy ćwiczenie pokazujące jak astronomowie wykorzystują paralaksę do pomiaru odległości międzygwiazdowych poprzez obliczenie odległości od „gwiazdy” znajdującej się w klasie. Z części materiałów dodatkowych można również pobrać krótki artykuł o historii pomiarów paralaks gwiazdw1.
Przedstawione przez nas ćwiczenie pokazuje podstawową geometrię pomiaru paralaksy przy pomocy nieskomplikowanych przyrządów do pomiaru kątów. Ćwiczenie, które zajmuje od 30 do 45 minut wraz z przygotowaniami, zostało pomyślnie przeprowadzone z uczniami w wieku od 13 do 17 lat. W kolejnym numerze Science in School opisana zostanie fotograficzna metoda pomiaru paralaksy, która jest jeszcze bardziej precyzyjna i rzeczywiście stosowana przez współczesnych astronomów.
Ćwiczenie: geometria paralaksy
Do wykonania poniższego ćwiczenia potrzebny będzie przyrząd do mierzenia kątów pomiędzy liniami wzroku – teodolit (zob. ryc. 1), jeśli takowy znajduje się na wyposażeniu gabinetu matematycznego, fizycznego czy geograficznego szkoły. Jeśli nie, podana zostanie instrukcja skonstruowania podobnego przyrządu mierzącego kąty z łatwo dostępnych materiałów.

Zdjęcie dzięki uprzejmości HdA / M Pössel
Materiały
- Dwa teodolity
- Mała kulka lub żarówka LED jako „gwiazda”
- Taśma miernicza
Jeśli nie masz dostępu do teodolitów, możesz przygotować proste przyrządy pokazane na ryc. 2. Dla każdego z nich (potrzebne będą dwa) potrzebne są:
- Kartka papieru
- Cienki, płaski karton o wymiarach około 4 cm x 8 cm
- Mały, drewniany klocek o wymiarach około 1 cm x 3 cm x 8 cm
- Stół lub inna pozioma powierzchnia

Zdjęcie dzięki uprzejmości HdA / M Pössel
Procedura
Ogólne ustawienie przyrządów pokazane jest na ryc. 3. Aby uprościć zadanie, wszystkie pomiary będą dokonywane na płaszczyźnie wyznaczonej przez punkty A, B i C, która powinna być równoległa do podłoża.

Zdjęcie dzięki uprzejmości HdA / M Pössel
Przygotowanie
- Podziel salę na dwie równe części rysując linię na podłodze, jak pokazano na ryc. 3. Prawa część sali z dwoma teodolitami (lub dwoma przyrządami własnej konstrukcji) to Ziemia, a lewa to kosmos.
- Umieść „gwiazdę” w części kosmos (pozycja A na ryc. 3). Za gwiazdę może posłużyć żarówka LED, ozdoba choinkowa, piłeczka do ping ponga lub inna mała kulka. Umieść gwiazdę w odpowiednim miejscu przy użyciu statywu, kija od miotły czy stojaka na parasole, bądź też podwieś ją pod sufitem.
Jeśli korzystasz z teodolitów, wykonaj następujące czynności:
- Ustaw teodolity na statywach, w części Ziemia. Należy ustawić stolik obrotowy każdego przyrządu tak, aby umieszczony był w poziomie (możesz użyć do tego poziomicy).
- Ustaw kąt deklinacji (odczytywany z białego półkola na ryc. 1) na zero. Sprawi to, że linie celowników (pokazane na ryc. 1) znajdą się w poziomie, w którym należy odczytywać kąty i długości.
- Dostosuj wysokość teodolitu do wysokości gwiazdy. Można to zrobić przy pomocy nóg teleskopowych w statywie teodolitu. Spójrz przez celowniki teodolitu i zmień wysokość statywu na taką, z której oddalona gwiazda będzie widoczna w prostej linii. Prawdopodobnie będzie konieczne ponownie ustawienie stolika obrotowego, ponieważ musi on się znajdować w pozycji poziomej.
Jeśli nie korzystasz z teodolitów, wykonaj własne przyrządy w następujący sposób:
- Przyklej kartkę papieru na każdym ze stołów lub na innych poziomych powierzchniach, dzięki czemu otrzymasz dwie platformy obserwacyjne odpowiadające teodolitom z ryc. 3.
- Ustaw celownik (linię, wzdłuż której patrzysz) przymocowując kawałek kartonu do brzegu drewnianego klocka, jak zostało to pokazane na ryc. 2.
- Dostosuj wysokość gwiazdy (znajdującej się w punkcie A na ryc. 3) w tai sposób, aby była ona dokładnie taka sama, jak wysokość obu przyrządów. Następnie w każdej z dwóch pozycji obserwacyjnych dopasuj pozycję celowników tak, aby można było spojrzeć na gwiazdę wzdłuż krawędzi kartonów.
Pomiary
Waszym zadaniem jest teraz obliczyć odległość pomiędzy punktem obserwacyjnym a gwiazdą, dokonując pomiarów jedynie z Ziemi. Nie chodzi oczywiście o to, aby rozciągnąć taśmę mierniczą pomiędzy punktami B i A, bo oznaczałoby to opuszczenie Ziemi. Nie możemy zmierzyć odległości, jaka dzieli nas od obiektów astronomicznych poza naszym Układem Słonecznym lecąc do nich.
Zamiast tego zmierzymy dwa kąty i długość jednego boku trójkąta ABC, a geometria pomoże nam ustalić długość dwóch pozostałych boków, AB i AC. Z pomocą teodolitu w punkcie B możemy zmierzyć kąt ABC w następujący sposób:
- Wyceluj teodolit B w kierunku teodolitu C. Odczytaj kąt azymutu na pierścieniu azymutalnym (czarna podziałka na stoliku obrotowym na ryc. 1). Najlepiej, aby oba teodolity były zwrócone do siebie w tym samym momencie.
- Teraz wyceluj teodolit B w gwiazdę w punkcie A. Ponownie odczytaj kąt azymutu.
- Odejmij jedna wartość azymutu od drugiej. W ten sposób otrzymasz wartość kata ABC.
- Powtórz czynność z teodolitem C, aby otrzymać kąt ACB.
- Na zakończenie zmierz odległość pomiędzy punktami B i C wzdłuż wyznaczonej linii z pomocą miary.
Jeśli korzystasz z własnych przyrządów, możesz dokonać tych samych pomiarów kątów, zaczynając od przyrządu B, w następujący sposób:
- Narysuj na przygotowanym papierze kropkę. Będzie ona twoim punktem odniesienia.
- Ustaw celownik w taki sposób, aby dolna krawędź kartonu stykała się z punktem odniesienia, a jego górna krawędź (wzdłuż której patrzysz) była wycelowana dokładnie w przyrząd w punkcie C. (Najlepiej, żeby oba przyrządy były w siebie wycelowane w tym samym momencie, i aby górne krawędzie ich kartonów były ustawione w jednej linii.)
- Zaznacz pozycję celownika rysując linię na papierze (jak pokazano na ryc. 2).
- Powtórz czynność celując przyrządem B w gwiazdę i po raz kolejny robiąc to przy pomocy górnej krawędzi kartonu, podczas gdy jego dolna krawędź przylega do punktu odniesienia, a następnie narysuj linię wzdłuż dolnej krawędzi.
- Przy pomocy kątomierza zmierz kąt pomiędzy dwoma narysowanymi liniami. Jest to kąt ABC.
- Powtórz czynność używając przyrządu C, patrząc najpierw na punkt B, a potem na A i narysuj linie. Otrzymasz w ten sposób kąt ACB.
- Na zakończenie zmierz odległość pomiędzy punktami B i C wzdłuż wyznaczonej linii przy pomocy miary.
Obliczanie odległości od gwiazdy
Znasz już kąty pomiędzy liniami biegnącymi do gwiazdy z dwóch punktów na Ziemi oraz odległość między tymi punktami. Jak zatem wykorzystać te wyniki do obliczenia odległości od gwiazdy? Na początku spójrz na geometryczne przedstawienie problemu na ryc. 4.
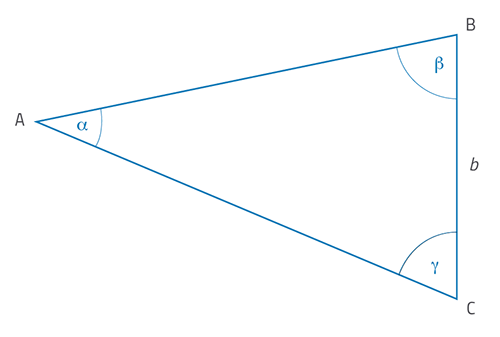
Zdjęcie dzięki uprzejmości HdA / M Pössel
Przedstawione w ten sposób pozycje gwiazdy A i teodolitów B i C znajdują się na poziomej płaszczyźnie i tworzą trójkąt ABC (widziany z góry). Kąty b i g odpowiadają zmierzonym kątom ABC i ACB, a odcinek b to wymierzona odległość pomiędzy B i C wzdłuż wyznaczonej linii.
Korzystając z wyników pomiarów, narysuj trójkąt w skali najdokładniejszej z możliwych: dobry rezultat uzyskasz w skali 1:50 na kartce A3. Następnie zmierz odcinki AB i AC na rysunku i przekształć ich długości w długości rzeczywiste, aby otrzymać odległości pomiędzy B i A oraz C i A.
Aby sprawdzić wynik, złam zasady! „Poleć w kosmos” i zmierz odcinki AB i BC taśmą mierniczą.
Na zakończenie przemyśl dokładność wyników uzyskanych dzięki pomiarom kątów. Gdybyśmy obliczali większe odległości, to czy dokładność wyników uległaby zmianie? Dlaczego?

Zdjęcie dzięki uprzejmości ESA / Gaia
Pomiary w kosmosie
Mamy nadzieję, że uczniom spodoba się odkrywcza natura przedstawionego ćwiczenia i że zrozumieją oni, w jaki sposób mierzy się odległości w astronomiiw1. Oczywiście prawdziwe procedury astronomiczne opierają się na skomplikowanych metodach, które muszą zapewnić największą możliwą precyzję, ponieważ gwiazdy znajdują się niemiernie daleko, a ich przesunięcia są nieznaczne. Nawet nasza najbliższa sąsiadka poza Układem Słonecznym (Proxima Centauri) jest oddalona o około 100 000 razy dalej niż najdłuższa odległość, jaką zmierzyć można na Ziemi – czyli podwójna odległość Ziemi od Słońca zakładająca pomiary oddzielone od siebie półletnią przerwą. Sytuacja porównywalna jest do próby pomiaru paralaksy obiektu oddalonego o 100 kilometrów przesuwając się zaledwie o metr.
Web References
Resources
- Poniżej przedstawiamy źródło dotyczące historii pomiaru paralaksy:
- Hirshfeld AW (2013) Parallax: The Race to Measure the Cosmos. Mineola, NY, USA: Dover Publications. ISBN: 9780486490939
- Eksperyment z paralaksą z użyciem zrobionego przez siebie przyrządu, jak w tym artykule, opisany jest tu:
- Ferguson JL (1977) More parallax without pain. American Journal of Physics 45(12): 1221-1222. doi: 10.1119/1.10697
- Informacje dotyczące przeprowadzania prawdziwych, astronomicznych pomiarów paralaksy z użyciem wielkich i małych teleskopów znajdziesz tu:
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46. doi: 10.1088/0143-0807/30/1/004
- Cenadelli D et al. (2016) Geometry can take you to the Moon. Science in School 35: 41-46.
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11/2014: 72-77
- Ratcliff SJ et al. (1993) The measurement of astronomical parallaxes with CCD imaging cameras on small telescopes. American Journal of Physics 61(3): 208. doi: 10.1119/1.17292
Review
Paralaksa gwiazd to najstarsza, najprostsza i najdokładniejsza metoda obliczania odległości do gwiazd. Artykuł wyjaśnia jak dokonać pomiarów naziemnych stosując tę metodę. Kierując się wskazówkami będziecie mogli zmierzyć odległości do obiektu, „gwiazdy” znajdującej się w klasie, a twoi uczniowie zrozumieją, w jaki sposób astronomowie wyznaczają ogromne odległości w kosmosie.





