La Parallasse: raggiungere le stelle con la geometria Teach article
Tradotto da Rocco G. Maltese. A che distanza troviamo le stelle? Impariamo, stando in classe, in quale modo gli astronomi misurano le distanze nello spazio.

della navicella spaziale Gaia,
con la Via Lattea sullo sfondo
Immagine cortesemente
concessa dall’ESA / ATG
medialab; immagine dello
sfondo: da ESO / S Brunier
Guardando dal finestrino di un’automobile o di un treno in movimento, ti accorgerai che la visuale degli oggetti cambia in relazione alla loro distanza: i cespugli o gli alberi vicini sembrano scorrere via rapidamente, mentre un albero che è ad una certa distanza sembra muoversi molto più lentamente.
Questa apparente variazione nella posizione dipendente dalla distanza detta parallasse. Potete riprodurre questo stesso effetto traguardando con il pollice della mano tesa davanti al viso, prima con l’occhio sinistro e poi con quello destro. A seconda dell’occhio utilizzato, il pollice sembra che salti da un posto all’altro in relazione alla distanza sullo sfondo verso cui vi ponete – questo perché i due occhi si trovano in due posizioni leggermente diverse una rispetto all’altra. Se muovete adesso il braccio, che precedentemente era steso, spostate il pollice più vicino al viso, ripetete l’esperimento traguardando prima con un occhio e poi con l’altro, a distanze diverse dal viso: noterete che la differenza di posizione apparente aumenta se la distanza tra il pollice e gli occhi diminuisce.
Questo effetto è stato utilizzato nei secoli per determinare le distanze nello spaziow1. A metà del 19-esimo secolo, gli astronomi utilizzando la parallasse, hanno ricavato le prime distanze delle stelle. Anche i cartografi hanno potuto utilizzare questa tecnica per creare carte geografiche più accurate della Terra. Attualmente, il satellite dell’ESA, Gaia, che è stato lanciato in orbita nel Dicembre 2013, sta misurando molto accuratamente le parallassi di più di un miliardo di stelle della nostra galassia, la Via Lattea, aumentando la precisione di queste osservazioni di circa un fattore 200.
In questo articolo descriviamo una esercitazione che spiega il modo in cui gli astronomi utilizzano la parallasse per determinare le distanze interstellari, ricavando la distanza di una “stella” in classe. Vi è del materiale di documentazione a disposizione che si può consultare e anche un breve articolo sul web, sulla storia della misura della parallasse che si può scaricare come materiale di documentazione dell’esercitazionew1.
L’esercitazione che descriviamo riproduce la geometria su cui si basano le misure delle parallassi, utilizzando semplici strumenti di misura degli angoli. Abbiamo successivamente utilizzato questa attività, che in tutto può durare dai 30 ai 45 minuti compreso il tempo di preparazione degli strumenti, con studenti di età compresa tra i 13 e 17 anni. Nel prossimo numero di Science in School, descriveremo un metodo fotografico per le misure delle parallassi, che è un metodo persino più accurato e astronomicamente più originale.
Esercitazione: la geometria alla base della parallasse.
Per questa esercitazione, necessiterete di uno strumento per la misura degli angoli tra la linee di vista – un teodolite (vedi figura 1), forse ne troverete uno tra la strumentazione di matematica, di fisica o di geografia. Se non lo troverete, vi forniremo qui di seguito, le istruzioni per costruirne uno simile, per misurare gli angoli, con del materiale di facile reperibilità.

Immagine cortesemente concessa da HdA / M Pössel
Materiali
- Due teodoliti
- Piccole sfere o LED che simuleranno le ‘stelle’
- Metro a nastro
Se non avete accesso ai teodoliti, potrete improvvisare, costruendo dei semplici strumenti come quelli mostrati in figura 2. Per ciascuno (ne avrete bisogno di due), avrete bisogno di:
- Un foglio di carta
- Un cartoncino sottile, piatto, di circa 4 cm x 8 cm
- Un piccolo blocco di legno, di circa 1 cm x 3 cm x 8 cm
- Un tavolo o un’altra superficie orizzontale

Immagine cortesemente concessa da HdA/ M Pössel
Procedura
La procedura base è illustrata nella figura 3. Per semplificare le cose, abbiamo eseguito tutte le misurazioni degli angoli nel piano definito dai punti A, B e C e parallelo al terreno.

Immagine cortesemente concessa da HdA / M Pössel
Preparazione
- Dividere la stanza in due sezioni mediante una linea disegnata a terra come quella mostrata in figura, dalla linea tratteggiata. La sezione alla destra della stanza che contiene il teodolite (o, altrimenti, dai due strumenti improvvisati) rappresenta la Terra, mentre la sezione a sinistra rappresenta lo spazio.
- Sistemare ‘la stella’ nella regione che abbiamo definito come spazio (posizione A in figura 3). Come stella possiamo utilizzare un LED, un addobbo natalizio, una palla da ping-pong o un’altra piccola sfera. Sistemate la stella come potete – usando un treppiede, su un manico di scopa in un porta ombrelli, o a partire dal soffitto.
Se state utilizzando un teodolite seguite le seguenti istruzioni:
- Sistemare i vostri due teodoliti, ciascuno montato su un treppiede, nella regione definita come Terra. AvrDovrete regolare il disco rotante di ciascun teodolite così che sia completamente orizzontale (potete utilizzare una livella ad alcool, se ne avete una a disposizione).
- Impostare a zero l’angolo di declinazione (letto sulla scala semicircolare in bianco riportato in figura 1). Questo conterrà la linea di vista (attraverso le viste in figura 1) all’interno del piano orizzontale, sul quale andremo a leggere tutti gli angoli e le distanze.
- Porre il teodolite alla stessa altezza di quella della stella. Potrete fare ciò utilizzando le gambe telescopiche del treppiede, sul quale avrete posto il teodolite, traguardate attraverso il mirino e regolate il treppiede sino a quando la stella è in direzione sulla linea di vista. Probabilmente bisognerà riaggiustare il disco rotante per essere sicuri che sia ancora orizzontale.
Se non state utilizzando i teodoliti, in alternativa, per regolare gli strumenti improvvisati seguite le seguenti istruzioni
- Incollate un foglio di carta su ciascuna delle tavole o altre superfici piane per creare due piattaforme di osservazione corrispondenti alle stesse posizioni B e C dei teodoliti della figura 3.
- Segnare la linea di “vista” (la linea lungo la quale effettuare l’osservazione) fissando il pezzo di cartone nello spigolo del blocco di legno, come mostrato in figura 2.
- Regolate l’altezza della vostra stella (posizione A in figura 3) così che si venga a trovarsi alla stessa altezza dal piano dei due visori. Quindi, da ciascuna delle vostre due posizioni, dovreste essere in grado di regolare la posizione del mirino così da guardare lungo il cartone da un lato, esattamente sul bordo, direttamente verso la stella.
Effettuare le osservazioni
Il vostro compito adesso è quello di determinando la distanza tra il vostro punto di osservazione e la stella, ponendovi per tutte le misurazioni esclusivamente nel settore denominato Terra. Ovviamente, non potrete semplicemente prendere il metro e allungarlo da B a A, poiché questo vorrebbe dire allontanarsi dalla Terra. Non possiamo misurare le distanze di oggetti astronomici al di fuori del Sistema Solare volando sino a la.
Invece misureremo, due angoli e la lunghezza di un lato del triangolo ABC, la geometria ci aiuterà a ricavare la lunghezza dei rimanenti due lati, AB e AC. Con il teodolite nella posizione B, possiamo misurare l’angolo ABC come descritto qui di seguito:
- Puntare l’obiettivo del teodolite-B nella direzione del teodolite-C. Leggere l’angolo sul disco di azimut (la linea sulla scala nera sul disco della figura 1). Questo funziona meglio se entrambi i teodoliti sono orientati uno nella direzione dell’altro allo stesso istante.
- Successivamente, puntare il visore del teodolite-B nella direzione della stella in A. Procedere alla lettura dell’angolo di azimut.
- Ripetere la procedura con il teodolite nella posizione C per ricavare l’angolo ACB.
- Finalmente, misuriamo la distanza tra i punti B e C lungo la linea di base usando il metro a nastro.
Con gli strumenti improvvisati, si possono effettuare le stesse misure angolari seguendo le istruzioni, prima per lo strumento nel punto B:
- Segnare un punto sul foglio di carta. Questo rappresenterà il vostro punto di riferimento.
- Porre il visore così che il lato inferiore del cartone tocchi il punto di riferimento, e il lato superiore (lungo il quale effettuerete l’osservazione) puntando direttamente verso l’altro dispositivo posto nel punto C. (Questo funzionerà meglio se i due dispositivi si guardano uno verso l’altro nello stesso istante, con il lato superiore dei loro cartoni allineati uno all’altro.)
- Segnare la posizione del visore disegnando una retta sul foglio (come mostrato in figura 2).
- Ripetere la procedura, cercando con lo strumento-B la stella posta nel punto A, traguardare quindi, lungo il lato superiore del cartone quello inferiore toccando il punto di riferimento, e segnare una retta lungo il lato inferiore.
- Usare il goniometro per misurare l’angolo tra le due rette che avete tracciato. Questo rappresenta l’angolo ABC.
- Ripetere la procedura, utilizzando lo strumento in C, guardando verso B e A a turno, segnando la linea di vista. Questa procedura fornirà l’angolo ACB.
- Finalmente, misurate la distanza tra i punti B e C lungo la linea di base, utilizzando il metro a nastro.
Ricavare la distanza stellare
Adesso conoscete gli angoli di vista della stella da due differenti posizioni della Terra, e in più la distanza, tra queste due posizioni. Come possiamo utilizzare questi risultati per determinare la distanza dalla stella? In primo luogo, diamo uno sguardo alla geometria della configurazione, come mostrata in figura 4.
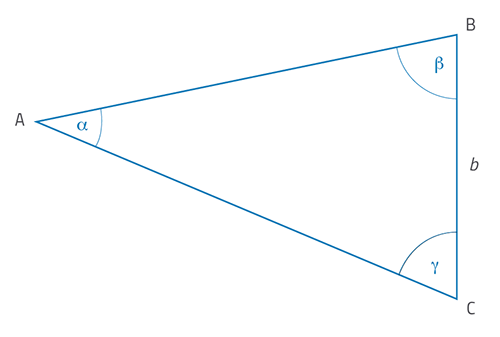
Immagine cortesemente fornita da HdA / M Pössel
Con questa configurazione, la posizione della stella in A, la posizione dei teodoliti in B e C, giacenti sul piano orizzontale formanti il triangolo ABC (visti dall’alto). Gli angoli b e g sono rispettivamente i valori degli angoli ABC e ACB, e la lunghezza b è la distanza misurata tra B e C lungo la linea di base.
Utilizzando le vostre misure, disegnate un diagramma in scala di un triangolo come questo il più accuratamente possibile: in scala di 1:50 su un foglio A3, si ottengono buoni risultati. Quindi semplicemente misurate le distanze AB e AC sul diagramma, e convertire queste in distanze reali per determinare le di distanze di B e C dalla stella A.
Per verificare i vostri risultati, rompiamo le regole! Viaggiamo nello “spazio” e utilizziamo il metro a nastro per misurare le distanze AB e BC.
Infine, discutiamo la precisione con la quale abbiamo ottenuto i risultati dalla misura dell’angolo. Se utilizziamo distanze più grandi, come varierà la precisione – e perché?

Immagine cortesemente concessa dall’ESA / Gaia
Effettuare le misure nello spazio
Noi speriamo che gli studenti apprezzino il senso della scoperta attraverso questa esercitazione, e si facciano un’idea di come si determinano le distanze in astronomiaw1. Naturalmente, le procedure astronomiche reali utilizzano dei metodi elaborati per poter assicurare la migliore precisione, poiché le stelle sono così distanti e la loro differenza di parallasse così minuscola. Persino la stella più vicine al di fuori del Sistema Solare (come Proxima Centauri) dista circa 100 000 volte più distanti della linea di base che può essere misurata sulla Terra – cioè, due volte la distanza tra la Terra e il Sole, se noi prendessimo delle immagini ad un intervallo di mezzo anno. Questo sarebbe come cercare di individuare una differenza di parallasse di un oggetto distante 100 chilometri quando ci spostiamo di un metro.
Web References
- w1 – Materiale di riferimento sulla storia della misura della parallasse possono essere scaricati dalla sezione riguardante il materiale aggiuntivo.
Resources
- Una fonte utile sulla storia delle misure di parallasse, vedi:
- Hirshfeld AW (2013) Parallax: The Race to Measure the Cosmos. Mineola, NY, USA: Dover Publications. ISBN: 9780486490939
- Un esperimento della misura della parallasse utilizzando uno strumento improvvisato per la misura degli angoli, come articolo, è descritto qui:
- Ferguson JL (1977) More parallax without pain. American Journal of Physics 45(12): 1221-1222. doi: 10.1119/1.10697
- Per informazioni su come calcolare misure reali di parallasse con telescopi astronomici, grandi e piccoli, vedi:
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46. doi: 10.1088/0143-0807/30/1/004
- Cenadelli D et al. (2016) La geometria ti può portare sulla Luna. Science in School 35.
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11/2014: 72-77
- Ratcliff SJ et al. (1993) The measurement of astronomical parallaxes with CCD imaging cameras on small telescopes. American Journal of Physics 61(3): 208. doi: 10.1119/1.17292
Review
La parallasse stellare è il metodo più antico e il più sicuro per determinare la distanza delle stelle. Questo articolo spiega come realizzare delle osservazioni terrestri utilizzando questo metodo. Se seguirete queste istruzioni, sarete in grado di misurare nella vostra classe di un oggetto, la “stella”, e i vostri studenti capiranno come gli astronomi calcolano le grandi distanze nello spazio.





