Balancing act: the physics of levers

We encounter various types of lever in our everyday lives: opening a drink with a bottle opener, cutting paper with scissors, taking the lid off a paint pot using a screwdriver, and – the simplest of all – playing on a seesaw in the park. Yet, the principle of levers is sometimes so natural to us that we do not pay any attention to how it actually works. 

In this easy game, pairs of students aged 11–19 take it in turns to add wooden blocks or objects to a tray balanced on a pivot. By competing to keep the tray level, students learn about the physics of levers – simple machines that make work easier by reducing the force needed to move a load. They can understand the moment of a force and the balance law of a lever (Haverlíková, 2011). 

Competitive students will strive to understand the basic principles so they can beat their opponents, and a practical game will enrich the learning process and contribute to a creative atmosphere in the classroom. The activity, including time for explanations and questions, will take around 1.5 hours.  

Physical principles of the lever 

Prior to the activity, introduce your students to the physical principles behind the lever. There are four basic elements to consider when using a lever:  

•     Pivot – the point around which something turns  
•     Beam – a wooden plank or solid rod that rests on the pivot
•     Load – the item or object being moved or lifted on the beam
•     Force – the effort or input needed to move the beam and the load

When you use a lever, you apply a turning force (the moment) around the pivot to move the load. Moments reduce the effort needed to move the load by increasing the distance over which it is acting. This explains why less force is needed to open a door by pushing at the side furthest from the hinge than at the side closest to the hinge. When you push at the hinge side of the door, you must apply more force because the distance is smaller.

A moment can be calculated using the following equation: 

M = F x d

where:  

M = moment of the force (Nm)

F = applied force (N)

d = perpendicular distance between the pivot and the point where the force is applied (m)

The balancing game 

Once students understand the physical principles behind the lever, they can consider how to use physics to win the game.

Materials

Working in pairs, each team will need:

• A tray (beam) – we used a plastic tray approximately 45 x 30 cm
• Cupboard handle or object with flat base and spherical top (pivot)
• Wooden building blocks or other objects (these act on the tray with force F) 

See figure 1 for example materials. 

Pre-game questions 

Before your students go head-to-head in the game, they can apply their knowledge of levers to answer the following questions: 

If you start off with a balanced tray, what would happen when you add an object to the tray? 

Depending on the weight of the object and where it is placed on the tray, there can be no visible effect, or the tray can rotate, tilt or fall over. 

An object is added to the balanced tray, making it tilt. Why? Where would the object need to be placed to cause the most tilting?

When an object is placed at a distance from the pivot, a moment is established, causing the tray to tilt. The moment of a force is directly proportional to the distance between the body and the pivot (M = F x d), so if the same object is placed further from the pivot, the tray will tilt more. If the object is placed at a distance too far from the pivot, the tray will tip and touch the table. The effect also depends on the weight (F) of the object. 

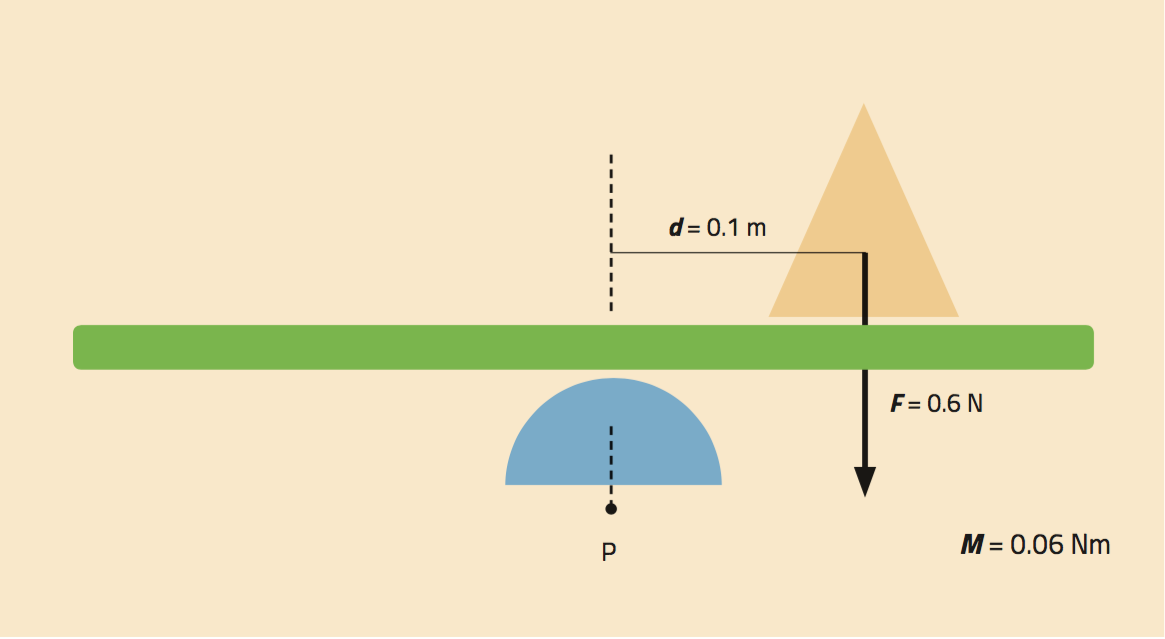
An example is shown in figure 2. If a load acting on the tray with a force of 0.6 N is placed at a distance of 0.1 m from the pivot, the moment may be calculated as follows:

M = F x d

    = 0.6 N x 0.1 m

    = 0.06 Nm

The resulting moment of force would make the tray tilt.

If we put the same load further from the pivot, e.g. 0.2 m away, the moment of force would increase to 0.12 Nm, which would cause the tray to tilt further or to touch the table.

Where should you place an object so that an empty or balanced tray remains balanced? 

When an object is placed on the pivot, the moment of force is equal to zero (d = 0) so there is no visible effect on the tray. 

Your opponent places an object on the tray, causing it to tilt. Where should you place your object to rebalance the tray?

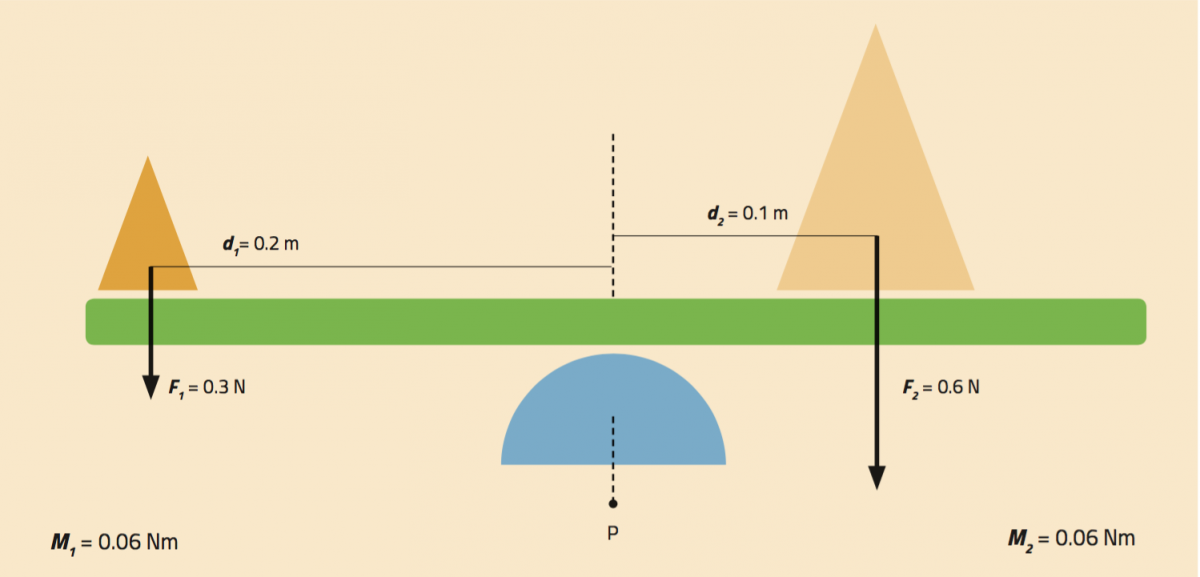
To keep the tray balanced, you must follow the physical principles related to the moment of a force. When an object is in equilibrium, the total anticlockwise moments should be equal to the total clockwise moments (F₁ x d₁ = F₂ x d₂). 

There are a few possibilities: 

• Place an identical object (same weight, same shape) opposite to your opponent’s object on the tray. It should be at the same distance from the pivot as the distance between the opponent’s object and the pivot.
• Place a lighter object opposite to your opponent’s object but at a greater distance from the pivot than their object. For example, an object two times lighter should be placed at a distance two times greater. 

In figure 3, the object that acts on the tray with a force of 0.3 N is two times lighter that the object opposite, which acts on the tray with a force of 0.6 N. If we want to balance the moment of force, the lighter object must be placed at a distance two times greater.

M₁= F₁ x d₁                                        M₂ = F₂ x d₂   

     = 0.3 N x 0.2 m                                   = 0.6 N x 0.1 m

     = 0.06 Nm                                           = 0.06 Nm

• Place a heavier object opposite to your opponent’s object but closer to the pivot than their object. 

If you keep the position of an object the same but vary the weight of the object, what is the effect on the moment? 

Placing a heavier object on the tray will cause the tray to tilt more. This is because the moment (M) is directly proportional to the applied force (F) and the perpendicular distance (d).  

Playing the game

After your students have considered the questions, they are ready to play the game.

1.  Balance the empty tray on the pivot (see figure 4), attempting to keep the tray as level as possible.
2.  Sitting opposite their opponent, students take it in turns to add an object to the tray from a shared pile of wooden building blocks or other objects. Allow 5 minutes to practice before starting the game.
3. The aim of the game is to keep the tray balanced. Students compete until one person places an object on the tray and causes it to tip and touch the table. The other student is the winner and gains one point.
4.  
   

   If neither student causes the tray to fall, and there are no more objects left in their pile, the students gain one point each.

5. Carry out a set of five games to determine the winner of the pair. The winners go on to the next round, making a new pair with another winner. The sets continue until there is only one winner.
6. Students who have been eliminated can support those who are still playing, or they can play for fun with other eliminated students.
7. Alternatively, to save time, use the scoring system to determine the highest scoring students from the first round. These students then compete in a final playoff, with the eliminated students as spectators.  

Basic rules

• During their turn, students can either add an object to the tray or change the position of an existing object on the tray.
• Only a single object can be placed on the tray at a time, and players can place only one object during their turn.
• Objects can be placed on top of each other.
• Players can skip a turn up to three times during the set, but a player cannot skip more than two successive turns.
• A piece of paper can be placed on the tray to increase friction between the tray and objects. This stops objects gliding off the tray when it tips. 

These rules can be varied, as agreed between the teacher and students.

Note: to increase the friction to stop the objects gliding off the tray when it tips, place a piece of paper on the tray.

Discussion

To encourage the students to think about the physical principles of levers and moments during the game, ask them some of the following questions: 

• How could you make the game more difficult for your opponent?
• Based on your experience, how could you advise your friend so they become the winner?
• What part of the game was most difficult?
• What most surprised you about the game?
• Did the position of the object on the tray matter?
• Did the weight of the object on the tray matter? 

You could repeat the pre-game questions to see if the activity has strengthened students’ understanding of the topic. 

Extension

You can increase the difficulty of the game by making some changes:

• Start by placing all the objects on the tray and in each turn, take away an object. Unlike when an object is added, the student cannot hold the object to estimate its weight and anticipate what will happen when they add it to the tray.
• Use a pointier pivot (e.g. place the tray on the tapered end of a hard-boiled egg or use an alternative cupboard handle) to reduce the surface area between the tray and the pivot.
• Use a smoother tray and a polished metal pivot to reduce friction.
• Use smoother objects to reduce the friction between the tray and the objects. The objects will glide on a tilted tray until it tips.
• Add or remove bigger, heavier, asymmetrical or inhomogeneous objects (an object that does not have the same weight in all parts) that cannot be placed on top of each other.
• Use a lighter tray so that the effect of adding an object is greater.
• Use a tray where the weight is not distributed equally (e.g. the four corners are heavier than the centre of the tray).

Acknowledgement

The activity was produced by Science on Stage Slovakia at the science centre SteelPark in Košice, Slovakia. Science on Stage^w1 is the network for European science, technology, engineering and mathematics (STEM) teachers, which was initially launched in 1999 by EIROforum, the publisher of Science in School. The non-profit association Science on Stage brings together science teachers from across Europe to exchange teaching ideas and best practice with enthusiastic colleagues from 25 countries.