Supporting materials
Download
Download this article as a PDF

Μετάφραση από Παναγιώτης Στασινάκης (Panagioits Stasinakis) Οι Pongprapan Pongsophon, Vantipa Roadrangka και Alison Campbell από το Πανεπιστήμιο Kasetsart στην Μπανγκόγκ της Ταϊλάνδης, παρουσιάζουν πώς…
«Η αρχή Hardy-Weinberg είναι η πιο δύσκολη έννοια για μένα. Ακόμα και τώρα, μετά από δέκα χρόνια διδασκαλίας, δεν έχω ξεκάθαρη εικόνα για αυτήν. Γνωρίζω πώς να λύνω προβλήματα σχετικά με την αρχή Hardy-Weinberg και μπορώ να την εξηγήσω στους μαθητές μου, αλλά… πραγματικά δεν μπορώ όμως να κατανοήσω γιατί τη χρησιμοποιούμε και πώς συσχετίζεται με την εξέλιξη. Για μένα, αυτό το πεδίο είναι περισσότερο μαθηματικά παρά βιολογία».
Κυρία Karnika, βιολόγος που διδάσκει στη δευτεροβάθμια εκπαίδευσης της Μπανγκόκ
Όταν, πριν από περίπου 150 χρόνια, ο Κάρολος Δαρβίνος γνωστοποίησε στο ευρύ κοινό τη θεωρία του για την εξέλιξη μέσω της φυσικής επιλογής, η ιδέα είχε μία σημαντική αδυναμία. Όπως οι περισσότεροι βιολόγοι της εποχής του, ο Δαρβίνος υπέθεσε πως τα χαρακτηριστικά των γονέων «αναμιγνύονταν» στους απογόνους τους. Σε διαδοχικές γενεές θα οδηγούσε στη μείωση της ποικιλομορφίας, προσφέροντας στη φυσική επιλογή ελάχιστο υλικό ποικιλότητας για να δράσει. Μία τυχαία συνάντηση ενός βιολόγου και ενός μαθηματικού σε έναν αγώνα κρίκετ περίπου 50 χρόνια μετά, έπαιξε σημαντικό ρόλο στην επίλυση αυτού του προβλήματος.
Τα πρώτα βήματα έγιναν στις αρχές του 20ου αιώνα, όταν ξαναμελετήθηκαν οι εργασίες του Γρηγόριου Μέντελ σχετικά με την κληρονόμηση στα φυτά. Ο τελευταίος είχε προτείνει πως τα χαρακτηριστικά είναι διακριτά (ξεχωριστά) και δεν αναμιγνύονται. Επίσης ο Μέντελ παρατήρησε πως αν και ένα χαρακτηριστικό φαίνεται να εξαφανίζεται σε μία συγκεκριμένη γενεά, συχνά αποκρύπτεται από ένα «επικρατές» χαρακτηριστικό – και επομένως μπορεί να επανεμφανιστεί, απαράλλαχτο σε μία επόμενη γενεά.
Πολλοί θεώρησαν πως αυτές οι ανακαλύψεις αντί να ενισχύουν τη Δαρβινική θεωρία, ήταν ασύμβατες με τη φυσική επιλογή. Αν οι μονάδες της κληρονομικότητας ήταν διακριτές, πώς θα μπορούσαν να παράγονται οι μικρές και συνεχείς παραλλαγές που παρατηρούνταν από τους βιολόγους; Και γιατί, αν ο Μέντελ ήταν σωστός, η συχνότητα των επικρατών χαρακτηριστικών δεν αυξάνονταν μέσα στον πληθυσμό;
Ανήμπορος να λύσει αυτό το τελευταίο πρόβλημα, ο Βρετανός Βιολόγος Reginald Punnett ζήτησε τη βοήθεια του G. Harold Hardy (με τον οποίο έπαιζαν κρίκετ). Ο Hardy ήταν μαθηματικός που γενικά αντιμετώπιζε με καταφρόνηση τα εφαρμοσμένα μαθηματικά. Το 1908, έγραφε στον επιμελητή της επιστημονικής επιθεώρησης Science:
«Είμαι απρόθυμος να ανακατευτώ σε μία συζήτηση που αφορά θέματα για τα οποία δεν έχω καμία εξειδικευμένη γνώση, και θα αναμένω η πολύ απλή λεπτομέρεια με την οποία θα πρέπει να καταπιαστώ, να γίνει οικεία στους βιολόγος. Παρόλα αυτά, ορισμένα σχόλια … με τα οποία ο κ. R. C. Punnett είχε τραβήξει την προσοχή μου, με έκαναν να πιστεύω πως ίσως έχει κάποια αξία να προσπαθήσω…»
Η «πολύ απλή λεπτομέρεια» που έπρεπε να αποδείξει ο Hardy, ήταν πως σε σχετικά μεγάλους πληθυσμούς όπου δεν υπάρχει ουσιαστικά μετανάστευση, τα ζευγαρώματα θα γίνονται τυχαία απουσία επιλογής και μεταλλαγής και οι συχνότητες των γονιδίων θα παραμένουν οι ίδιες. Η ποικιλομορφία θα μπορούσε να διατηρηθεί κατά τη διάρκεια των γενεών.
Η «αρχή του Hardy» αποτελούσε μία συνεισφορά στην συνύπαρξη της Δαρβινικής φυσικής επιλογής και της γενετικής του Μέντελ, που αναπτύχθηκε σταδιακά στις δεκαετίες του 1920 και 1930 για να δημιουργηθούν οι νέες ιδέες σχετικά με την εξέλιξη.
Το 1943 η αρχή έγινε γνωστή ως αρχή Hardy-Weinberg (ή ισορροπία ή νόμος των Hardy-Weinberg), όταν διαπιστώθηκε πως η ίδια ιδέα είχε ήδη προταθεί ανεξάρτητα το 1908, από το γερμανό ιατρό, Wilhelm Weinberg.*
Σήμερα, η επιστήμη της πληθυσμιακής γενετικής, της οποίας είναι μέρος, παρέχει την πιο σημαντική θεωρητική βάση για την εξελικτική βιολογία και μπορεί να χρησιμοποιηθεί για να δοκιμαστούν σχεδόν όλες οι εξελικτικές ιδέες.
*Αργότερα διαπιστώθηκε πως ένας αμερικανός, ο William Castle, είχε προτείνει μία ανάλογη ιδέα το 1903.
Dean Madden, Εθνικό Κέντρο για τη Βιοτεχνολογική Εκπαίδευση, Ηνωμένο Βασίλειο
Η αρχή των Hardy-Weinberg είναι ένα από τα πιο δύσκολα ζητήματα στην εξέλιξη, για πολλούς καθηγητές και μαθητές (Mertens, 1992). Ίσως έχουν ένα φόβο για τα μαθηματικά και τις ποσοτικές προσεγγίσεις της πληθυσμιακής γενετικής και πιθανόν δεν έχουν τη δυνατότητα να εφαρμόσουν την αρχή για να εξηγήσουν τα βιολογικά φαινόμενα. Αρκετοί από αυτούς αναρωτιούνται πια να είναι άραγε η σχέση μεταξύ της αρχής Hardy-Weinberg και της κατανόησης της εξέλιξης. Για να βοηθήσω την κ. Karnika καθώς και άλλους εκπαιδευτικούς που αντιμετωπίζουν τις ίδιες δυσκολίες, θα ήθελα να σας παρουσιάσω τη δραστηριότητα Μετρώντας Κουμπιά. Πρόκειται για μία απλή αναπαράσταση της ισορροπίας Hardy-Weinberg και το πώς η φυσική επιλογή επηρεάζει τη συχνότητα των αλληλομόρφων μέσα σε ένα πληθυσμό. Αυτή η δραστηριότητα είναι κατάλληλη για μαθητές δευτεροβάθμιας εκπαίδευσης και φοιτητές, που διδάσκονται εξέλιξη. Η δραστηριότητα αναπτύχθηκε εξ’ ολοκλήρου από το προσωπικό του Τμήματος Γενετικής στο Πανεπιστήμιο Kasetsart της Ταϊλάνδης και αργότερα τροποποιήθηκε, ως μέρος μίας διδακτορικής διατριβής, για να χρησιμοποιηθεί με μαθητές δευτεροβάθμιας εκπαίδευσης.

Η εξέλιξη είναι αλλαγή στις γονιδιακές συχνότητες ενός πληθυσμού κατά τη διάρκεια του χρόνου (Skelton, 1993; Strickberger, 1996). Ένας πληθυσμός είναι ομάδα ατόμων του ίδιου είδους που ζει σε μία συγκεκριμένη περιοχή, του οποίου τα μέλη μπορούν να διασταυρώνονται και επομένως να μοιράζονται μία κοινή ομάδα γονιδίων, γνωστή ως γονιδιακή δεξαμενή. Κάθε γονιδιακή δεξαμενή περιέχει όλα τα αλληλόμορφα, για όλα τα χαρακτηριστικά όλων των ατόμων. Η συχνότητα των αλληλομόρφων είναι ο αριθμός των αλληλομόρφων ενός συγκεκριμένου τύπου, ως αναλογία του συνολικού αριθμού των αλληλομόρφων για αυτό το χαρακτηριστικό. Το 1908, οι Hardy και Weinberg κατασκεύασαν ένα μοντέλο ενός πληθυσμού ο οποίος δεν εξελίσσεται και διευθέτησαν τις συνθήκες στις οποίες ένας τέτοιος πληθυσμός θα μπορούσε να υπάρξει (Abedon, 2005): a large ένας πληθυσμός με πολλά άτομα που δεν μεταναστεύουν, δεν έχουν μεταλλάξεις, δεν ασκείται φυσική επιλογή και παρατηρείται τυχαίο ζευγάρωμα. Αν παρακολουθήσουμε τις συχνότητες των αλληλομόρφων ενός πληθυσμού σε διαδοχικές γενιές και βρούμε ότι οι συχνότητες των αλληλομόρφων παρεκκλίνουν από τις τιμές που αναμένουμε σύμφωνα με την ισορροπία Hardy-Weinberg, τότε ο πληθυσμός εξελίσσεται.
Η δραστηριότητα Μετρώντας Κουμπιά προσομοιάζει έναν πληθυσμό σε γενετική ισορροπία και έναν πληθυσμό που υφίσταται φυσική επιλογή. Η φυσική επιλογή δρα στους φαινοτύπους των οργανισμών: φυσικά χαρακτηριστικά, μεταβολισμό, φυσιολογία και συμπεριφορά, «και προσαρμόζει έναν πληθυσμό στο περιβάλλον του, αυξάνοντας ή διατηρώντας τους ευνοϊκούς γονότυπους στη γενετική δεξαμενή» (Campbell & Reece, 2002). Σε ένα μεταβαλλόμενο περιβάλλον, η φυσική επιλογή ευνοεί κάθε υπάρχοντα γονότυπο που έχει ήδη προσαρμοστεί στις νέες συνθήκες.
Σημείωση προς τους εκπαιδευτικούς: Οι εκπαιδευτικοί θα πρέπει να διαπιστώσουν αν οι μαθητές τους κατανοούν τη Μεντελική γενετική, ειδικά τις μονοϋβριδικές διασταυρώσεις, πριν πραγματοποιήσουν αυτή τη δραστηριότητα. Αυτή είναι μία δραστηριότητα για ομάδες τεσσάρων ή πέντε μαθητών, και μπορεί να διαρκέσει μέχρι και τρεις ώρες.
Αφού έχουν ολοκληρώσει αυτή τη δραστηριότητα, οι μαθητές θα έχουν προσομοιώσει έναν πληθυσμό σε γενετική ισορροπία και θα έχουν εξετάσει την επίδραση της φυσικής επιλογής στη συχνότητα των αλληλομόρφων ενός πληθυσμού κατά τη διάρκεια πέντε γενεών.
Κάθε κουμπί αντιπροσωπεύει ένα διπλοειδές άτομο, μέσα σε έναν πληθυσμό. Κάθε πλευρά του κουμπιού, αντιπροσωπεύει ένα αλληλόμορφο: το μαύρο-μαύρο είναι ένα άτομο με γονότυπο RR, το μαύρο-λευκό είναι Rr, και το λευκό-λευκό είναι rr.
Κάθε ζευγάρι κουμπιών, θα παράγει τέσσερις απογόνους: οι γονότυποι των απογόνων καθορίζονται από τον πρώτο νόμο του Μέντελ.
Πείραμα Ι: ένας πληθυσμός σε ισορροπία
Πείραμα ΙΙ: ένας πληθυσμός που εξελίσσεται
Υποθέστε πως τα άτομα με το γονότυπο rr πεθαίνουν πριν κατορθώσουν να αναπαραχθούν. Πρέπει επομένως να εξαλείψετε τα κουμπιά λευκό/λευκό από κάθε γενεά μετά την πρώτη.
Σημείωση: Οι μαθητές ίσως βρουν, πως σε ορισμένους γύρους υπάρχει ένα μοναχικό μη ζευγαρωμένο κουμπί στο κουτί μετά την επιλογή ζευγαριών κουμπιών. Αυτό το μοναχικό κουμπί θα πρέπει να απομακρυνθεί από τον πληθυσμό καθώς δεν έχει καμία πιθανότητα να ζευγαρώσει με άλλα άτομα.
Τους πλήρεις πίνακες μπορείτε να τους κατεβάσετε από την ιστοσελίδαw1 του Science in School.
| No. | Γονότυποι γονέων | Γονότυποι απογόνων | ||||
|---|---|---|---|---|---|---|
| PR | Rr | rr | ||||
| 1 | → | |||||
| 2 | → | |||||
| 3 | → | |||||
| 4 | → | |||||
| 5 | → | |||||
| Γενιές | Αριθμός κάθε γονότυπου | Συχνότητα αλληλομόρφου R | Συχνότητα αλληλομόρφου r | ||
|---|---|---|---|---|---|
| RR | Rr | rr | |||
| 0 | 16 | 32 | 16 | 0.5 | 0.5 |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| Γενιές | Αριθμός κάθε γονότυπου | Συχνότητα αλληλομόρφου R | |||
|---|---|---|---|---|---|
| RR | Rr | Frequency of allele rrr | |||
| 0 | 16 | 32 | 16 | 0.5 | 0.5 |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
Όταν δεν υπάρχει επιλεκτική πίεση, η συχνότητα των δύο αλληλομόρφων αυξομειώνεται ελαφρώς (Πίνακας 5). Όταν υπάρχει μία εξελικτική πίεση έναντι του ομόζυγου υπολειπόμενου γονότυπου (δηλαδή, αν τα rr άτομα πεθάνουν πριν αναπαραχθούν), η συχνότητα του αλληλομόρφου r στον πληθυσμό μειώνεται με το πέρας του χρόνου (Πίνακας 6).
| NO. | Γονότυποι γονέων | Γονότυποι απογόνων | ||||
|---|---|---|---|---|---|---|
| RR | Rr | rr | ||||
| 1 | RR | Rr | → | 2 | 2 | 0 |
| 2 | → | |||||
| 3 | → | |||||
| 4 | → | |||||
| 5 | → | |||||
| Γενιά | Αριθμός κάθε γονοτύπου | Συχνότητα αλληλομόρφου R | Συχνότητα αλληλομόρφου r | ||
|---|---|---|---|---|---|
| RR | Rr | rr | |||
| 0 | 16 | 32 | 16 | 0.5 | 0.5 |
| 1 | D1 = 17 | H1 = 34 |
R1 = 13 |
0.53 | 0.47 |
| 2 | D2 = 14 | H2 = 35 | R2 = 15 | 0.49 | 0.51 |
| 3 | D3 = 16 | H3 = 32 | R3 = 16 | 0.50 | 0.50 |
| 4 |
D4 = 15 |
H4 = 31 |
R4 = 18 |
0.48 | 0.52 |
| 5 | D5 = 16 |
H5 = 33 |
R5 = 15 | 0.50 | 0.50 |
| Γενιά | Αριθμός κάθε γονοτύπου |
Συχνότητα αλληλομόρφου R |
Συχνότητα αλληλομόρφου r | ||
|---|---|---|---|---|---|
| RR |
Rr |
rr | |||
| 0 | 16 | 32 | 16 | 0.5 | 0.5 |
| 1 |
D1 = 21 |
H1 = 29 | R1 = 14 | 0.55 | 0.45 |
| 2 | D2 = 30 | H2 = 24 | R2 = 10 | 0.65 | 0.35 |
| 3 | D3 = 36 | H3 = 21 | R3 = 17 | 0.72 | 0.28 |
| 4 | D4 = 41 |
H4 = 17 |
R4 = 6 | 0.77 | 0.23 |
| 5 | D5 = 48 |
H5 = 12 |
R5 = 4 |
0.84 | 0.16 |
D = επικρατές
H = ετερόζυγος
R = υπολειπόμενο
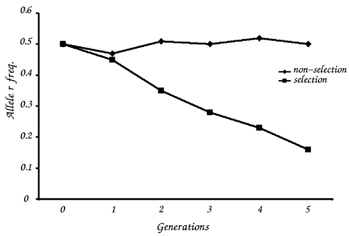
Συγρίνετε τις γραφικές παραστάσεις συχνοτήτων των αλληλομόρφων από τον σταθερό και τον εξελισσόμενο πληθυσμό. Διαφέρουν;
Πώς η φυσική επιλογή επηρεάζει τις συχνότητες των αλληλομόρφων ενός πληθυσμού κατά τη διάρκεια του χρόνου;
Ένα επικρατές αλληλόμορφο ενός χαρακτηριστικού, εμφανίζεται πάντοτε σε μεγαλύτερη συχνότητα σε ένα πληθυσμό και ένα υπολειπόμενο αλληλόμορφο έχει πάντα τη μικρότερη συχνότητα; Εξήγησε την απάντησή σου.
Οι εκπαιδευτικοί θα πρέπει να έχουν υπόψη τους πως οι μαθητές ίσως δεν ερμηνεύουν καλά τις γραφικές παραστάσεις, εστιάζοντας αποκλειστικά σε δύο ή τρία σημεία και δεν παρατηρούν πως υπάρχουν διακυμάνσεις από γενιά σε γενιά. Ο εκπαιδευτικός θα πρέπει επιπλέον να δώσει έμφαση πως σε έναν φυσικό πληθυσμό απαιτούνται συνήθως περισσότερες από πέντε γενιές πριν μπορέσουμε να καταγράψουμε οποιαδήποτε αλλαγή στη συχνότητα των αλληλομόρφων. Η εξέλιξη χρειάζεται χρόνο.
Μετά τη διεξαγωγή του δεύτερου πειράματος, ορισμένοι μαθητές ίσως συμπεράνουν πως η φυσική επιλογή πάντα αυξάνει τη συχνότητα ενός επικρατούς αλληλομόρφου και μειώνει τη συχνότητα ενός υπολειπόμενου αλληλομόρφου στον πληθυσμό. Ωστόσο, δεν οδηγούν όλες οι επιλογές σε σταδιακή μείωση των υπολειπόμενων αλληλομόρφων. Το αλληλομόμορφο – επικρατές ή υπολειπόμενο – το οποίο επιλέγεται, σχετίζεται πάντα με τις υπάρχουσες περιβαλλοντικές συνθήκες. Προκειμένου να αποφύγετε την παρανόηση, είναι επιθυμητό για τον εκπαιδευτικό να ρωτήσει τους μαθητές για περιπτώσεις όπου το υπολειπόμενο αλληλόμορφο είναι κοινό ενώ το επικρατές σπάνιο: η ομάδα αίματος Ο είναι ένα υπολειπόμενο χαρακτηριστικό αλλά η πλειονότητα των ανθρώπων σε ορισμένους πληθυσμούς έχει αυτή την ομάδα αίματος, η ασθένεια Huntington είναι ένα επικρατές χαρακτηριστικό αλλά μόνο 4-10 άτομα στους 100000 την εμφανίζουν. Περισσότερα παραδείγματα άλλων ειδών φυσικής επιλογής περιγράφονται στο O’Neil (2006).

Το «Μετρώντας Κουμπιά» είναι μία απλή και απτή δραστηριότητα για να αποδείξετε την αρχή Hardy-Weinberg. Οι μαθητές, με την εμπλοκή τους σε αυτή τη δραστηριότητα θα κατορθώσουν να εμβαθύνουν σε πληθυσμό που βρίσκεται σε ισορροπία και στη φυσική επιλογή ως μία δύναμη για βιολογική προσαρμογή. Οι μαθητές θα εφαρμόσουν τους νόμους του Μέντελ και μαθηματικές δεξιότητες για να αξιοποιήσουν τα δεδομένα και να ερμηνεύσουν τα αποτελέσματα. Το «Μετρώντας Κουμπιά» είναι ένα παράδειγμα για το πώς να διδάξουμε βιολογία με έναν ενιαίο τρόπο και να χρησιμοποιήσουμε μαθηματικά για να κατανοήσουμε περίπλοκα βιολογικά φαινόμενα.
«Το Μετρώντας Κουμπιά με βοήθησε να αντιληφθώ την αρχή Hardy–Weinberg. Τώρα μπορώ να εξηγήσω στους μαθητές μου για ποιό λόγο χρησιμοποιείται η αρχή και πώς να τη συσχετίσουν με άλλα πεδία που διαθέτουν εξελικτικό περιεχόμενο. Αισθάνομαι μεγαλύτερη αυτοπεποίθηση και διασκεδάζω να διδάσκω αυτό το θέμα. Προφανώς, οι μαθητές έδειξαν μεγαλύτερο ενδιαφέρον για το μάθημα. Ήταν χαρούμενοι που εργάστηκαν πρακτικά και συνεργάστηκαν σε αυτή την εργαστηριακή άσκηση».
Κυρία Karnika, αφού υλοποίησε τη δραστηριότητα το «Μετρώντας Κουμπιά»
w1 – Όλοι οι απαραίτητοι πίνακες μπορούν να προσπελασθούν από εδώ.
Για κάθε επίπεδο, η αρχή Hardy-Weinberg είναι μία δυσνόητη έννοια. Είναι πραγματικά απίθανο να δεις πώς ακριβώς δρα και πώς ίσως η επιλογή επηρεάζει τη συχνότητα των αλληλομόρφων. Αυτή η πρωτότυπη ιδέα ενεργούς μάθησης, μίας φαινομενικά αφαιρετικής έννοιας, προσομοιάζει πώς η αρχή Hardy-Weinberg μπορεί να εφαρμοστεί τόσο σε έναν σταθερό όσο και σε έναν εξελισσόμενο πληθυσμό. Τα κουμπιά αντιπροσωπεύουν ομόζυγους και ετερόζυγους γονότυπους επικρατών και υπολειπόμενων αλληλομόρφων, οι οποίο γονότυποι χρησιμοποιούνται για να αξιολογήσουν την κατανόηση της Μεντελικής γενετικής και στη συνέχεια να διερευνήσουν πώς μεταβάλλεται η γονιδιακή συχνότητα σε σταθερούς και εξελισσόμενους πληθυσμούς.
Τρεις ώρες για όλη την δραστηριότητα είναι ένας λογικός υπολογισμός. Η δραστηριότητα θα μπορούσε να είναι ιδανική για δύο χωριστά μαθήματα: ένα για τον σταθερό πληθυσμό και ένα για τον εξελισσόμενο πληθυσμό. Αυτό θα εμποδίσει τους μαθητές να βαρεθούν καθώς τραβούν κουμπιά από τις σακούλες ή να μπερδευτούν από τα διαφορετικά μαθηματικά που απαιτούνται για να μοντελοποιηθεί κάθε πληθυσμός. Τα μαθηματικά για τον εξελισσόμενο πληθυσμό απαιτούν ιδιαίτερη συγκέντρωση για να γίνουν κατανοητά και ίσως οι μαθητές χρειαστούν χρόνο για να κάνουν τους υπολογισμούς
Οι ερωτήσεις για συζήτηση θα μπορούσαν να αποτελέσουν αφορμή για ανταλλαγή ορισμένων καλών ιδεών. Τα σημεία που αναφέρθηκαν για την επιλογή των αλληλομόρφων θα μπορούσαν να αναδείξουν την ανάγκη συνειδητοποίησης ορισμένων επικρατών και υπολειπόμενων γενετικών ασθενειών και θα μπορούσαν να χρησιμοποιηθούν για περαιτέρω έρευνα, ίσως συνδέοντάς τα με τη γενετική μηχανική και τη γενετική διάγνωση και, αν το επιτρέπει ο χρόνος, τη συζήτηση σχετικά με την ηθική της επιλογής.
Shelley Goodman, Ηνωμένο Βασίλειο
Download this article as a PDF