Παράλλαξη: φτάνοντας στα αστέρια με την γεωμετρία Teach article
Μετάφραση από την Αιμιλία Ξανθοπούλου (Emily Xanthopoulos). Πόσο μακριά βρίσκονται τα αστέρια; Εξερευνήστε στην τάξη σας το πως μετρούν οι αστρονόμοι τις αποστάσεις στο…

αναπαράσταση του
διαστημόπλοιου Gaia (Γαία),
με τον Γαλαξία μας στο
βάθος
Η εικόνα είναι ευγενική
χορηγία του ESA / ATG
εργαστηρίου των μέσων
ενημέρωσης· η εικόνα του
φόντου: ESO / S Brunier
Κοιτάξτε έξω από ένα παράθυρο ενός κινούμενου αυτοκινήτου η τρένου, και θα παρατηρήσετε ότι η θέα σας για τα αντικείμενα αλλάζει με την απόσταση τους: κοντινοί θάμνοι η δέντρα φαίνονται σαν να περνούν βιαστικά, ενώ ένα μακρινό δέντρο η κτήριο φαίνεται σαν να κινείται πολύ πιο αργά.
Αυτή η φαινομενική αλλαγή στην θέση που εξαρτάται από την απόσταση ονομάζεται παράλλαξη. Μπορείτε να αναπαράγετε το φαινόμενο κάνοντας το σημάδι του “like/μπράβο” με τον αντίχειρα πάνω και μπροστά από το πρόσωπο σας και κοιτώντας τον αντίχειρα σας πρώτα μόνο με το αριστερό σας μάτι, και μετά μόνο με το δεξί σας μάτι. Καθώς αλλάζετε μάτια, ο αντίχειρας σας φαίνεται να μετακινείται προς τα πλάγια σε σχέση με τις πιο απομακρυσμένες εικόνες στο βάθος – γιατί τα δυο σας μάτια είναι σε ελαφρώς διαφορετικές θέσεις. Τώρα τεντώστε το χέρι σας όσο πιο μακριά πάει και, πλησιάζοντας τον αντίχειρα προς το πρόσωπο σας, επαναλάβετε το πείραμα κοιτάζοντας με κάθε μάτι χωριστά σε διάφορες αποστάσεις: θα παρατηρήσετε ότι η μετατόπιση στην προφανή θέση αυξάνεται καθώς η απόσταση μεταξύ του αντίχειρα και των ματιών σας μειώνεται.
Αυτό το φαινόμενο χρησιμοποιείται αιώνες τώρα για να προσδιοριστούν οι αποστάσεις στο διάστημαw1. Στα μέσα του 19ου αιώνα, οι αστρονόμοι χρησιμοποίησαν την παράλλαξη για να υπολογίζουν τις πρώτες αστρικές αποστάσεις. Οι τοπογράφοι χρησιμοποιούν επίσης αυτού του είδους την μέτρηση για να σχεδιάσουν ακριβείς χάρτες της επιφάνειας της Γης. Αυτή την στιγμή, ο δορυφόρος Gaia (Γαία) του ESA, που εκτοξεύτηκε τον Δεκέμβριο του 2013, μετρά εξαιρετικά ακριβείς παραλλάξεις για περισσότερο από ένα δισεκατομμύριο άστρα στον Γαλαξία μας, αυξάνοντας την ακρίβεια κατά ένα συντελεστή περίπου 200.
Σε αυτό το άρθρο, περιγράφουμε μια δραστηριότητα, που εξερευνά τον τρόπο με τον οποίο οι αστρονόμοι χρησιμοποιούν την παράλλαξη για να μετρήσουν τις διαστρικές αποστάσεις, υπολογίζοντας την απόσταση ‘ενός αστεριού‘ που έχει στηθεί σε μια τάξη. Υπάρχει επίσης ένα σύντομο άρθρο στο διαδίκτυο για την ιστορία των μετρήσεων της παράλλαξης, που μπορείτε να κατεβάσετε από το τμήμα με το επιπλέον υλικόw1.
Η δραστηριότητα που περιγράφουμε εδώ αναπαράγει την βασική γεωμετρία των μετρήσεων παράλλαξης, χρησιμοποιώντας απλά όργανα για να μετρήσουμε τις γωνίες. Χρησιμοποιήσαμε με επιτυχία αυτή την δραστηριότητα, η οποία διαρκεί 30 με 45 λεπτά συμπεριλαμβανομένου και του στησίματος της διάταξης, με μαθητές με ηλικίες μεταξύ 13 και 17. Στο επόμενο τεύχος του Science in School, θα περιγράψουμε μια φωτογραφική μέθοδο που χρησιμοποιεί μετρήσεις παράλλαξης η οποία είναι ακόμη πιο ακριβής και αστρονομικά αυθεντική.
Δραστηριότητα: η γεωμετρία της παράλλαξης
Για αυτή την δραστηριότητα, θα χρειαστείτε ένα όργανο για την μέτρηση των γωνιών ανάμεσα στις οπτικές γραμμές – έναν θεοδόλιχο (δείτε την εικόνα 1), αν υπάρχει ένας στον σχολικό σας εξοπλισμό για τα μαθηματικά, την φυσική η την γεωγραφία. Αν όχι, δίνουμε εδώ οδηγίες για το πως να κατασκευάσετε ένα παρόμοιο εργαλείο μέτρησης γωνιών από υλικά που είναι εύκολα διαθέσιμα.

Η εικόνα είναι ευγενική χορηγία του HdA / M Pössel
Υλικά
- Δύο θεοδόλιχοι
- Μια μικρή σφαίρα η LED (δίοδος εκπομπής φωτός) ως το ‘άστρο’
- Μεζούρα
Αν δεν έχετε πρόσβαση σε θεοδόλιχους, μπορείτε να αυτοσχεδιάσετε κατασκευάζοντας τα απλά όργανα που φαίνονται στην εικόνα 2. Για το καθένα (θα χρειαστείτε δύο), θα χρειαστείτε:
- Ένα φύλλο χαρτιού
- Λεπτό, επίπεδο χαρτόνι, περίπου 4 εκ. x 8 εκ.
- Ένα μικρό ξύλινο κομμάτι, περίπου 1 εκ. x 3 εκ. x 8 εκ.
- Ένα τραπέζι η μια άλλη οριζόντια επιφάνεια

Η εικόνα είναι ευγενική χορηγία του HdA / M Pössel
Διαδικασία
Η βασική διάταξη φαίνεται στην εικόνα 3. Για να απλουστεύσουμε τα πράγματα, κάνουμε όλες τις γωνιακές μετρήσεις στο επίπεδο που ορίζεται από τα σημεία Α, Β και C, τα οποία πρέπει να είναι παράλληλα με το έδαφος.

Η εικόνα είναι ευγενική χορηγία του HdA / M Pössel
Διάταξη
- Χωρίστε το δωμάτιο σε δύο τμήματα ζωγραφίζοντας μια γραμμή στο έδαφος, όπως φαίνεται από την διακεκομμένη γραμμή. Το δεξί τμήμα του δωματίου με τους δύο θεοδόλιχους (η εναλλακτικά με τα αυτοσχέδια όργανα) αντιπροσωπεύει την Γη, ενώ το τμήμα στα αριστερά αντιπροσωπεύει το διάστημα.
- Τοποθετήστε το ‘άστρο’ στην περιοχή του διαστήματος (θέση Α στην εικόνα 3). Ως άστρο, μπορείτε να χρησιμοποιήσετε ένα LED (μια δίοδο), ένα χριστουγεννιάτικο στολίδι, μια μπάλα του πινγκ πονγκ η μια άλλη μικρή σφαίρα. Στήστε το άστρο όπως μπορείτε – χρησιμοποιώντας ένα τρίποδο, σε μια λαβή σκούπας, σε μια ομπρελοθήκη, η από το ταβάνι.
Ακολουθήστε τα βήματα της διάταξης παρακάτω αν χρησιμοποιείτε θεοδόλιχους:
- Στήστε του δυο σας θεοδόλιχους, καθέναν πάνω στο τρίποδο του, στην περιοχή της Γης. Θα χρειαστεί να ρυθμίσετε την περιστρεφόμενη βάση κάθε θεοδόλιχου έτσι ώστε να είναι τελείως οριζόντια (χρησιμοποιήστε το αλφάδι αν έχει ένα ο θεοδόλιχος).
- Βάλτε την γωνία απόκλισης (ανάγνωση από την άσπρη ημικυκλική κλίματα στην εικόνα 1) στο μηδέν. Αυτό διατηρεί τις ορατές γραμμές (μέσω των σκοπευτών στο σχήμα 1) μέσα στο οριζόντιο επίπεδο, στο οποίο θα λαμβάνουμε όλες τις μετρήσεις γωνίας και μήκους.
- Ρυθμίστε το ύψος του θεοδόλιχου ώστε να είναι το ίδιο με αυτό του αστεριού. Μπορείτε να το κάνετε αυτό χρησιμοποιώντας τα τηλεσκοπικά πόδια του τρίποδου του θεοδόλιχου. Με το αστέρι να βρίσκεται σε κάποια απόσταση από τον θεοδόλιχο, κοιτάξτε από τα σκόπευτρα και ρυθμίστε το τρίποδο μέχρι το αστέρι να βρίσκεται απευθείας σε θέα ευθείας γραμμής. Πιθανώς να χρειαστεί να ξαναπροσαρμόσετε την περιστρεφόμενη βάση ώστε να βεβαιωθείτε ότι είναι ακόμη οριζόντια.
Διαφορετικά, αν δεν χρησιμοποιείτε θεοδόλιχους, ακολουθήστε αυτά τα βήματα για να κάνετε τα αυτοσχέδια όργανα:
- Τοποθετήστε ένα φύλλο χαρτιού σε καθένα από τα τραπέζια η τις άλλες επίπεδες επιφάνειες για να δημιουργήσετε δύο πλατφόρμες παρατήρησης που θα αντιστοιχούν στις θέσεις Β και C του θεοδόλιχου στην εικόνα.
- Κάντε την ‘οπτική γραμμή’ (την γραμμή κατά μήκος της οποίας βλέπετε) σταθεροποιώντας το χαρτόνι στην πλευρά του ξύλινου κομματιού, όπως φαίνεται στην εικόνα2.
- Ρυθμίστε το ύψος του αστεριού σας (θέση Α στην εικόνα 3) έτσι ώστε να είναι ακριβώς στο ίδιο ύψος πάνω από το έδαφος όπως η γραμμή ορατότητας του θεοδόλιχου. Τότε, από κάθε μια από τις δύο θέσεις σας, θα μπορείτε να ρυθμίζετε την θέση της ορατότητας έτσι ώστε να μπορείτε να βλέπετε κατά μήκος της κάρτας από το πλάι, ακριβώς πάνω στην άκρη, κατευθείαν προς το άστρο.
Παίρνοντας τις μετρήσεις
Η εργασία σας τώρα είναι να προσδιορίσετε την απόσταση ανάμεσα στo σημείο παρατήρησης σας και το άστρο, κάνοντας όλες τις μετρήσεις σας μόνο από την Γη. Προφανώς, δεν μπορείτε απλά να αρπάξετε την μεζούρα και να την τεντώσετε από το σημείο Β στο σημείο Α, γιατί αυτό θα σήμαινε ότι θα φεύγατε από την Γη. Δεν μπορούμε να μετρήσουμε τις αποστάσεις των αστρονομικών σωμάτων έξω από το Ηλιακό μας σύστημα πετώντας μέχρι εκεί.
Αντί αυτού, θα μετρήσουμε τις δύο γωνίες και το μήκος της μιας πλευράς του τριγώνου ΑΒC, και η γεωμετρία θα μας βοηθήσει να βρούμε το μήκος των άλλων δύο πλευρών, ΑΒ και ΑC. Με τον θεοδόλιχο στην θέση Β, μπορούμε να μετρήσουμε την γωνία ΑΒC ως εξής:
- Στρέψτε το σκόπευτρο του Β-θεοδόλιχου προς την κατεύθυνση του C-θεοδόλιχου. Διαβάστε την γωνία αζιμούθιου στον δίσκο αζιμούθιου (την μαύρη κλίμακα στην περιστρεφόμενη βάση στην εικόνα 1). Αυτό λειτουργεί καλύτερα αν και οι δύο θεοδόλιχοι είναι στραμμένοι ο ένας προς τον άλλο ταυτόχρονα.
- Στην συνέχεια, στρέψτε το σκόπευτρο του Β-θεοδόλιχου προς την κατεύθυνση του αστεριού Α. Ξανά, διαβάστε την γωνία αζιμούθιου
- Αφαιρέστε την μια από τις αζιμούθιες τιμές από την άλλη, Αυτό σου δίνει την τιμή της γωνίας ΑΒC..
- Επαναλάβετε την διαδικασία με τον θεοδόλιχο στην θέση C για να μετρήσετε την γωνία ΑCΒ.
- Τέλος, μετρήστε την απόσταση ανάμεσα στα σημεία Β και C κατά μήκος της γραμμής βάσης χρησιμοποιώντας την μεζούρα.
Με τα αυτοσχέδια όργανα, οι ίδιες γωνιακές μετρήσεις μπορούν να εκτελεστούν ως εξής, πρώτα για το όργανο στο Β
- Σημειώστε μια κουκίδα στο χαρτί. Αυτό θα είναι το σημείο αναφοράς σας.
- Τοποθετήστε το στόχαστρο έτσι ώστε η κάτω πλευρά του χαρτονιού να αγγίζει το σημείο αναφοράς, και η πάνω πλευρά (κατά μήκος της οποίας βλέπεις) να δείχνει απευθείας στο άλλο όργανο που έχει τοποθετηθεί στο C. (Αυτό λειτουργεί καλύτερα αν τα δύο όργανα είναι στραμμένα το ένα προς το άλλο ταυτόχρονα, με τις πάνω πλευρές των χαρτονιών σκοπεύτρων ευθυγραμμισμένες μεταξύ τους.)
- Σημειώστε την θέση του σκοπεύτρου σχεδιάζοντας μια γραμμή πάνω στο χαρτί (όπως φαίνεται στην εικόνα 2).
- Επαναλάβετε την διαδικασία, κοιτάζοντας με το Β όργανο προς το αστέρι Α, ξανά στοχεύοντας κατά μήκος της επάνω πλευράς του χαρτονιού με την κάτω πλευρά να ακουμπά το σημείο αναφοράς, και σχεδιάζοντας μια γραμμή κατά μήκος της κάτω πλευράς.
- Χρησιμοποιήστε ένα μοιρογνωμόνιο για να μετρήσετε την γωνία ανάμεσα στις δύο γραμμές που έχετε σχεδιάσει. Αυτή είναι η γωνία ΑΒC.
- Επαναλάβετε την διαδικασία, χρησιμοποιώντας το όργανο στο C, κοιτώντας προς το Β και το Α με την σειρά, και σημειώνοντας τις γραμμές στόχευσης. Αυτή θα δώσει την γωνία ΑCΒ.
- Τέλος, μετρήστε την απόσταση ανάμεσα στα σημεία Β και C κατά μήκος της γραμμής βάσης χρησιμοποιώντας την μεζούρα
Βρίσκοντας την απόσταση του αστεριού
Ξέρετε τώρα τις οπτικές γωνίες του αστεριού από δύο διαφορετικές θέσεις στην Γη, και επίσης την απόσταση ανάμεσα σε αυτές τις θέσεις. Πως μπορούμε τώρα να χρησιμοποιήσουμε αυτά τα αποτελέσματα για να υπολογίσουμε την απόσταση του αστεριού; Πρώτα από όλα, δείτε την γεωμετρία της κατάστασης, όπως φαίνεται στην εικόνα 4.
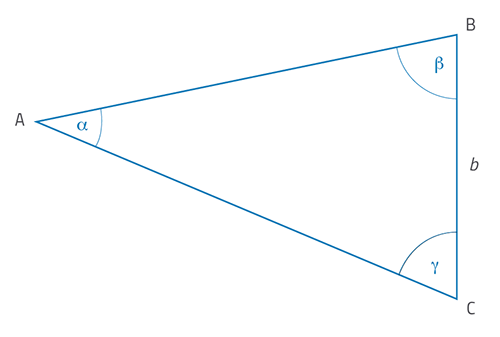
Η εικόνα είναι ευγενική χορηγία του HdA / M Pössel
Σε αυτή την διάταξη, η θέση Α του αστεριού και οι θέσεις του θεοδόλιχου Β και C βρίσκονται όλες σε ένα οριζόντιο επίπεδο και δημιουργούν το τρίγωνο ΑΒC (όπως φαίνεται ακριβώς από πάνω). Οι γωνίες β και γ είναι οι μετρούμενες γωνίες ΑΒC και ΑCΒ, αντίστοιχα, και το μήκος b είναι η μετρούμενη απόσταση ανάμεσα στο Β και C κατά μήκος της γραμμής βάσης.
Χρησιμοποιώντας τις δικές σας μετρήσεις, σχεδιάστε ένα διάγραμμα σε κλίμακα ενός τέτοιου τριγώνου όσο το δυνατόν πιο ακριβές: μια κλίμακα 1:50 σε χαρτί A3 δίνει καλά αποτελέσματα. Μετά απλά μπορείτε να μετρήσετε τις αποστάσεις ΑΒ και ΑC από το διάγραμμα, και να τις μετατρέψετε σε αληθινές αποστάσεις για να προσδιορίσετε τις αποστάσεις του Β και C από το αστέρι Α.
Για να ελέγξετε τα αποτελέσματα σας, σπάστε τους κανόνες! Ταξιδέψτε μέσα στο ‘διάστημα’ και χρησιμοποιήστε την μεζούρα για να μετρήσετε τα ΑΒ και ΒC.
Τέλος, συζητήστε για την ακρίβεια των αποτελεσμάτων που επιτεύχθηκαν με την γωνιακή μέτρηση. Αν είχαμε χρησιμοποιήσει μεγαλύτερες αποστάσεις, πως θα άλλαζε αυτή η ακρίβεια – και γιατί;

Η εικόνα είναι ευγενική χορηγία του ESA / Gaia
Μετρήσεις στο διάστημα
Ελπίζουμε ότι οι μαθητές θα απολαύσουν μια αίσθηση ανακάλυψης από αυτή την δραστηριότητα, και θα πάρουν μια ιδέα του τρόπου με τον οποίο γίνονται οι μετρήσεις απόστασης στην αστρονομίαw1. Φυσικά, οι πραγματικές αστρονομικές διαδικασίες χρησιμοποιούν περίπλοκες μεθόδους ώστε να εξασφαλίσουν την καλύτερη δυνατή ακρίβεια, διότι τα αστέρια βρίσκονται πολύ μακριά και οι μετατοπίσεις της παράλλαξης τους είναι τόσο μικρές. Ακόμη και ο πιο κοντινός μας αστρικός γείτονας έξω από το Ηλιακό μας Σύστημα (ο Εγγύτατος του Κενταύρου, Proxima Centauri) βρίσκεται μερικές 100 000 φορές πιο μακριά από την μεγαλύτερη απόσταση γραμμής βάσης που μπορεί να μετρηθεί από την Γη – δηλαδή, διπλάσια από την απόσταση μεταξύ της Γης και του Ήλιου, αν πάρουμε φωτογραφίες σε χρονικό διάστημα μισού χρόνου. Αυτό είναι σαν να προσπαθούμε να εντοπίσουμε μια μετατόπιση παράλλαξης ενός αντικειμένου που βρίσκεται 100 χιλιόμετρα μακριά όταν κάνουμε ένα βήμα ενός μέτρου στο πλάι.
Web References
- w1 – Μπορείτε να κατεβάσετε υλικό σχετικά με την ιστορία των μετρήσεων παράλλαξης από το διαδίκτυο από το τμήμα του επιπλέον υλικού.
Resources
- Για μια χρήσιμη πηγή σχετικά με την ιστορία των μετρήσεων παράλλαξης, δείτε το:
- Hirshfeld AW (2013) Parallax: The Race to Measure the Cosmos. Mineola, NY, USA: Dover Publications. ISBN: 9780486490939
- Ένα πείραμα παράλλαξης χρησιμοποιώντας ένα αυτοσχέδιο όργανο γωνιακών μετρήσεων, όπως στο άρθρο, περιγράφεται εδώ:
- Ferguson JL (1977) More parallax without pain. American Journal of Physics 45(12): 1221-1222. doi: 10.1119/1.10697
- Για πληροφορίες σχετικά με το πώς να κάνετε πραγματικές μετρήσεις αστρονομικής παράλλαξης με αστρονομικά τηλεσκόπια, μεγάλα και μικρά, δείτε τα:
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46. doi: 10.1088/0143-0807/30/1/004
- Cenadelli D et al. (2016) Geometry can take you to the Moon. Science in School 35: 41-46.
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11/2014: 72-77
- Ratcliff SJ et al. (1993) The measurement of astronomical parallaxes with CCD imaging cameras on small telescopes. American Journal of Physics 61(3): 208. doi: 10.1119/1.17292
Review
Η αστρονομική παράλλαξη είναι η πιο παλιά, πιο απλή και πιο ακριβής μέθοδος για να καθορίσουμε τις αποστάσεις των αστεριών. Αυτό το άρθρο εξηγεί πώς να κάνετε επίγειες μετρήσεις χρησιμοποιώντας αυτή την μέθοδο. Αν ακολουθήσετε τις οδηγίες, θα μπορέσετε να μετρήσετε μέσα από την τάξη σας την απόσταση ενός σώματος, του ‘αστεριού’, και οι μαθητές σας θα καταλάβουν πως οι αστρονόμοι μπορούν να υπολογίσουν τεράστιες αποστάσεις στο διάστημα.





