Fantastic feats: magic with money Teach article
You’ll need to put your money on the table for this batch of tricks, then use your scientific knowledge to make ‘cents’ of what happens!

In this third ‘fantastic feats’ article, we present some entertaining challenges involving money – and, of course, some physics along the way. One-cent coins from the USA and aluminium coins from various countries are especially useful for these activities – so if you encounter these on your holiday this summer, perhaps bring some back with you.
Feat 1: Jumping coin
Can you get a coin to jump into a cup without using your hands? Remarkably, the answer is yes – just by using the power of your breath. The challenge is to get the coin to ‘jump’ into the cup by blowing hard enough.
After you have succeeded, you can try to calculate the minimum breath speed needed to get the coin into the cup. You can also repeat the trick – and the calculation – with other coins.
Materials
- One small, light coin – if possible made from aluminium (e.g. Chinese yen)
- Other small coins (optional)
- Small match box
- Cup or mug, preferably with sloping sides
- A table or other level surface
Procedure
- Set up the coin, match box and mug as shown in figure 1.
- Position yourself as shown in figure 1, so that your breath will go straight over the coin.
- Blow quickly and forcefully – the coin should ‘jump’ into the mug (figure 2).
- For additional fun, the coins can be made to do a ‘high jump’ or ‘long jump’, by using pencils stacked up or laid next to each other, instead of the cup.
David Featonby
reduction in air pressure above it.
David Featonby
Discussion
How does fast-moving air manage to lift the coin into the cup, when there is nothing pushing up from below? The explanation lies in Bernoulli’s principle – the same idea that explains how aircraft wings gain lift by moving fast through air. This principle states that when the speed of air (or any fluid) increases, its pressure decreases. So here, the fast-moving breath leads to a reduction in air pressure above the coin, which lifts the coin into the mug.
Mathematically, Bernoulli’s principle can be stated thus:
P + ½ ∂ v2 = constant
where:
P = pressure (force exerted divided by the area on which it is exerted)
∂ = density of the fluid (air)
v = velocity of the moving object or fluid
So
P1 + ½ ∂ v02 = P2 + ½ ∂ v2
The pressure difference between stationary air (v0 = 0) and moving air (v) is thus:
P1 – P2 = ½ ∂ v2
The uplift force due to the reduced pressure is:
(P1 – P2) x A (where A = area of coin)
= A x ½ ∂ v2 (from above)
The force required to lift the coin is m x g (where m = mass of coin, and g = acceleration due to gravity, approximately 9.8 m s–2)
This means that the coin’s weight is balanced when
½ ∂ v2 x A = m x g
We can therefore calculate the minimum speed (vmin) of breath needed to lift the coin:
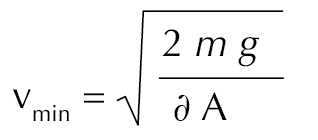
For circular coins, A = πr2
For a Chinese yen (mass = approximately 1 g, diameter = 20 mm)
Density of air = 1.225 kg/m3
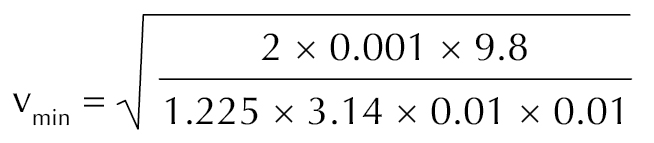
= 7.2 m/s
For a euro one-cent coin (mass = 2.3 g, diameter 16.25 mm)

= 13.32 m/s
For a euro five-cent coin (mass = 3.9 g, diameter 21.25 mm)
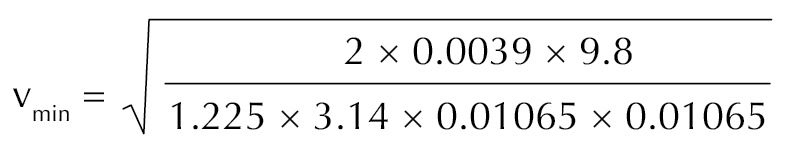
= 13.23 m/s
Note that these last two values are very similar. Can you show that coins of the same thickness and material will have the same lifting velocity, no matter what their diameter is?
Feat 2: Water pile-up
This feat involves another property of fluids: surface tension. We use a coin as a base on which to ‘pile up’ water. The challenge is to get as many drops of clean water from a dropper onto a clean coin without spilling any off the edge of the coin. You can carry out this feat as a contest to see who can get the most drops on a coin – but be sure everyone has coins and droppers of the same size.
Materials
Each person or group will need the following:
- One small copper coin (a euro one-cent coin is ideal)
- Dropper (e.g. a pipette or syringe)
- Clean water
- A table or other level surface
Procedure
- Most coins that have been handled are quite greasy, so first wash the coin in hot soapy water, then rinse and dry it thoroughly. The detergent also needs to be removed completely.
- Fill the dropper with clean water.
- Hold the dropper over the coin (without touching it) and place a drop of water on the coin (figure 3).
- Keep on placing water drops onto the coin, counting the number of drops as you go. The water will pile up over the surface of the coin, but eventually it will spill over. Note how many drops you added before this happened (figure 4).
- What’s the highest number of drops you can place on the coin? Try the challenge again to find your personal best – or find out what others managed and try to beat them!
- As an extra challenge, try to work out what will happen if you add soap or detergent to the water pile on the coin. Think about it and make a note of your prediction – then touch the water gently with a piece of soap or a drop of detergent. What happens – and why?
David Featonby
David Featonby
Discussion
It should be possible to put approximately 40 drops onto a clean coin, although this number will vary considerably with the cleanliness of the water and the size of the coin. But as water is liquid, why does it stay on the coin at all, rather than flowing over the sides?
The answer, of course, is surface tension: forces of attraction between molecules in the water act like a ‘skin’ to hold the water together on the coin. Although these forces are quite weak, they really do affect how liquids behave – as this activity shows. Surface tension is also what causes drops of liquid to form a spherical shape, minimising their surface area.
However, dirt on the surface of the coin can reduce the surface tension of the water dropped onto it, meaning that fewer drops can be added: the water does not ‘pile up’, but spreads out over the surface. And when the water is contaminated by soap or detergent, the surface tension forces are greatly reduced. As the drops are no longer held together, only a few drops can be placed on the coin before they flow over the coin’s edge.
Feat 3: Heads versus tails
This activity is not really a feat or a physical challenge – but it does challenge our notion of a ‘fair’ coin.
We all know that coins have two sides – heads and tails – and that the chance of a tossed coin landing one particular side up (heads, say) is 50%. But while this assumption is widely held, and relied upon in situations ranging from football match kick-offs to probability questions in maths, is it really true in practice?
For most coins, the answer is probably ‘yes, just about’ – but it’s not true for all coins. In particular, US one-cent coins are not perfectly balanced between their two sides: the ‘tail’ side is marginally heavier than the ‘heads’ side. This means that, given a perfectly fair spin, these coins will land heads-up significantly more often than tails-up.
In this activity, we use an ingenious method that effectively tosses 50 coins at once – revealing in a single action whether that type of coin is fair or not.
Materials
- A large number (e.g. 50) of identical low-value coins, preferably US one-cent coins
- A table or other level surface
Procedure
- Place the coins flat on the table.
- Balance all the coins on their edges, one by one, facing in different directions (figure 5).
- When the coins are all balanced, hit the table sharply with your fist (figure 6). The coins will fall over onto their faces – either the heads or tails side.
- Separate the coins into those that landed heads-up and those that landed tails-up (figure 7). How many are there of each? Do you think the coin is fair – or biased?
- If possible, repeat the activity with another set of a different coin. If you are going abroad for a summer holiday, perhaps try to bring back a set of coins to try.
coins balanced on their edges
David Featonby
the table is hit sharply
David Featonby
after sorting – showing many
more ‘heads’, as the ‘tails’
side is lightly heavier
David Featonby
Discussion
Tossing a coin, as at the beginning of a football match, does not reveal whether the coin is fair or not, as the way in which the coin is tossed has more effect on how it lands than any slight mass difference between the two sides. The challenge is to give the coin a totally neutral spin, giving it an equal chance to land on either side – if it is truly fair. Here, we do this by balancing 50 or so coins on their edges and seeing how many fall each way.
If you are lucky enough to have a set of US one-cent coins, you should have been able to witness how far from fair this seemingly normal coin is. If you are interested in probability and statistics, you can try posing and answering follow-up questions with your students, such as:
- What is the probability of your result (numbers of heads and tails) occurring purely by chance?
- Is your result statistically significant? (Assume p < 0.05 for significance.)
- From your results, can you work out the probability of a single toss of this coin landing (i) heads, or (ii) tails?
As far as we know, based on our experiments, no coin other than the US one-cent coins has a sufficient mass difference for this effect to be reliably observed. So here is a further challenge: by obtaining coins from countries around the world and repeating this balancing experiment, can you find any other coins that are significantly biased? If so, please write and tell us!
Resources
- Read an accessible article illustrating Bernoulli’s principle, complete with several demonstrations, from Wired magazine.
- Explore fluid dynamics and the Bernoulli equation with an online app.
- Watch a video from Physics Girl, which shows some fun experiments demonstrating surface tension.
- Read about a study of biased coins from the Smithsonian magazine.
Review
This article describes some activities that illustrate some basic principles in physics – particularly the Bernoulli principle and the surface tension of fluids. One wonderful feature in the Bernoulli activity is that it includes the mathematics needed to calculate the physical parameters involved.
As well as providing practical activities for a physics class with interesting explanations, the article could be used as a basis for class discussion. Suggested questions include:
- What is the Bernoulli principle, and what terms does the Bernoulli equation include?
- Using the Bernoulli principle, can you explain how aircraft wings gain lift?
- How can you decrease the surface tension of water?
- Some insects such as the pond-skater (or water strider) can run over water. How do they do this?
Gerd Vogt, physics and technology teacher, Higher Secondary School for Environment and Economics, Yspertal, Austria





