What do we know about climate? Investigating the effects of anthropogenic global warming Understand article
In this, the second of two articles, climate researcher Rasmus Benestad from the Norwegian Meteorological Institute examines the evidence that humans are causing climate change.
It is well established that there is a natural greenhouse effect on Earth that makes the planet inhabitable. So what about anthropogenic global warming (AGW)? After all, natural climate variations existed long before man intervened; just look at the ice ages.
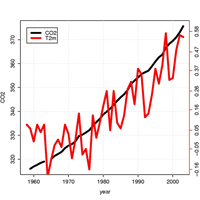
concentrations (black; from
Mauna Loa, Hawaii) and the
global mean temperature (T(2m)
orange, but no scale provided;
data from NASA GISS).
Click on image to enlarge
Image courtesy of Rasmus Benestad
From theoretical considerations, you would expect that temperature would increase if heat loss was inhibited while energy supply was constant. Increasing the concentrations of greenhouse gases (GHGs) has the same effect as restricting heat loss, as GHGs are transparent to sunlight but opaque to the infra-red light that constitutes Earth’s heat loss to space. Thus, an increased greenhouse effect disrupts the radiative energy balance.
The primary empirical evidence for an ongoing climate change includes a ~30% systematic increase in CO2 levels since a pre-industrial level of 280 parts per million (the black curve in this figure shows CO2 levels since 1958). There is no doubt that the CO2 is from fossil sources, as isotope ratios show that the carbon has been less exposed to galactic cosmic rays (GCRs).
When protons from GCRs collide with the nitrogen-14 (seven protons plus seven neutrons in the nucleus) in the air, carbon-14 is created (in addition to other isotopes such as beryllium-10) through a nuclear reaction:
14N + p → 14C + n
This means that carbon with a low isotope carbon-14 ratio must come from deep in the ground, out of reach of cosmic rays.
Furthermore, the ratio of O2 to N2 has diminished. This is expected from the increased combustion of fossil fuels, in which O2 combines with C to form CO2. The oceans have also become more acidic, leading to an increase in CO2 levels in both the atmosphere and the oceans.

Rob Friedman
After all, carbon cannot spontaneously vanish from the face of Earth – under normal circumstances, it is conserved. Hence, the burning of fossil fuels is expected to produce a surplus of CO2 somewhere in the atmosphere, oceans and/or the biosphere. Extracting fossil carbon from deep underground removes it from these hidden reservoirs and releases it to the surface of Earth, where it remains.
According to the Fourth Assessment Report (AR4) from the Intergovernmental Panel on Climate Change (IPCC), the global mean temperature, estimated from thousands of individual thermometers scattered around the globe, has increased by 0.74 ± 0.18 ºC over the past 100 years, and appears to be rising still. Some satellite-based studies have also reported changes in the spectral characteristics of the heat radiated from Earth, in line with an increased greenhouse effect. Bore-hole measurements from below the surface can also be used to infer temperature changes, and these too indicate that there has been a warming.
The global mean sea level is increasing, both due to the fact that warmer water has greater volume and because glaciers have melted. It has also been documented that most glaciers worldwide have retreated since the end of the 19th century. The sea-ice cover in the Arctic has diminished substantially since satellite measurement began, and the snow extent has decreased too.
There is also evidence from the hydrologic cycle: signs of more frequent intense downpours, and changes in the river discharge and rainfall statistics.
Additional reports on biological responses fit into the picture of a global climate change. Changes in the tree line, tree ring widths/density, corals, sea-bottom sediments and stalagmites bear witness to how the climate has varied in the past. Compared with these indicators, the present warming seems to be exceptional for at least the past 1000 years.
Doubts?
Those who dispute the notion of an AGW, popularly called climate sceptics, have argued that global warming is a consequence of changes in the Sun. But modern measurements of cosmic rays, sunspots and other indices used to describe the state of the Sun suggest that it has not become more active since the 1950s (see graph).
Variations to the Sun’s behaviour would not necessarily exclude the role of GHGs in climate change. If our climate were to be sensitive to slight changes in the Sun, then it would suggest that our climate is easily affected by changes in the energy balance – hence a stronger reason to think that changes in GHGs could cause a global climate change.
Other factors may affect the radiation balance, such as changes in Earth’s orbit around the Sun, and solar activity. Volcanoes are known to inject particles into the upper atmosphere that block sunlight, and natural as well as anthropogenic aerosols may also have a ‘dimming’ effect, reducing the amount of energy from the Sun that reaches Earth’s surface. Aerosols may also affect Earth’s heat loss – the net effect depends on the type of particle, their size, altitude and concentration.
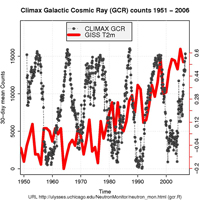
cosmic rays (GCRs; grey) and
the global mean temperature
(T(2m); blue). Although there
is no long-term trend in GCR
behaviour, the T(2m) has risen.
Click on image to enlarge
Image courtesy of Rasmus Benestad
Changes in land surface may also play a role by changing the way the planet reflects light as well as the exchange of moisture and energy between the surface and the atmosphere.
Some sceptics argue that global warming is an illusion due to the effect of urbanisation. However, this does not explain how most of the world’s oceans have warmed both near the surface and at depths – where there are no cities. Nor does it explain why the greatest warming has been observed in the Arctic, Alaska and Siberia. Besides, the urban influence on the temperature record has been studied and taken into account when estimating the global mean.
Another argument used by climate sceptics is that satellite measurements of the temperature in the atmosphere do not show similar warming as on the ground. This discrepancy was due to errors in the analysis of the satellite data; the trends in the free atmosphere have now been reconciled with the surface data.
Others have argued that our atmosphere is already opaque to infra-red radiation and is hence saturated, so any additional CO2 will not have much effect. However, one only has to look to Venus to see that the atmosphere doesn’t saturate that easily. One can also show this theoretically. Besides, it is not only the effect of CO2 that matters, as there are important feedback processes which may amplify (such as retreating sea ice, or air moisture) or dampen (low clouds, for example) the response to a changing greenhouse effect.
But hasn’t the climate always been changing? There are scholars who argue that our climate has a naturally cyclic behaviour. How do we know that the present warming is not just a part of a natural cycle, such as a rebound from a short ice age?
We can deduce from the laws of physics that the mean temperature does not just change spontaneously, as heat must be conserved. In the past, something in particular caused the variations – be it changes in the Earth’s solar orbit, atmospheric composition, solar activity, volcanoes or landscape changes. None of these factors, except for changes in GHG concentrations, can explain the current warming. Even changes to the system itself, such as El Niño Southern Oscillations, may produce some variations, but these tend to be weak compared with the changes due to external forces. And regardless of cause, there is always a physical explanation for the changes, be it external or internal.
Can we really trust global climate models (GCMs)? GCMs are not perfect, but they are still the best tool available for making projections for the future. A GCM may be thought of as a jigsaw puzzle, where the large picture emerges from small pieces put together in a consistent and organised manner. GCMs incorporate everything we know about the climate system in terms of physical laws and empirical data, and provide a comprehensive picture through the means of numerical methods on large computers. Some equations describing the processes cannot be solved exactly, but approximations nevertheless provide a good representation.
Projections for the future
So what can we expect from an AGW? The scientific findings published in peer-reviewed scientific journals have been collected and assessed in the IPCC’s report, which then presents the main picture for the future.
According to the AR4, an AGW will very likely result in a general warming, with a stronger response in the Arctic and over the continents. In the sub-tropics, there may be more droughts, but higher latitudes are expected to receive more precipitation. The report suggests that there will be more floods and famines. The glaciers may melt, reducing the supply of drinking water for a large part of the world’s population. A sea-level rise will affect low-lying coastal land areas, and in some regions people may be forced to move to higher ground.
The hurricane season of 2005 produced an unprecedented number – at least in modern times – of tropical cyclones in the Caribbean/North Atlantic, some of which resulted in substantial casualties and severe damages. Will there be more frequent or more powerful hurricanes/typhoons when the world is warmer? And are we now witnessing a trend in tropical cyclone activity? At present, we cannot be sure, although there are some indications that the potential for storm intensity may rise, and that there has been an upward trend in the activity associated with the more intense tropical cyclones over some ocean basins.
Condensation trails

This MERIS (MEdium Resolution Imaging Spectrometer) shows much of north-eastern Europe, including areas of Germany, Sweden, Poland and Denmark.
The elongated clouds around and to the east of Denmark, particularly visible over the sea, are in fact condensation trails formed by water vapour from aeroplanes. The number of contrails reflects the high level of air traffic in the skies. It is thought that these contrails can form high-altitude cirrus clouds, which could contribute towards global warming.
Work within ESA’s Data User Element (DUE) currently includes studies into condensation trails and any effects they might have on climate change.
Social aspects
In addition to the scientific issues surrounding AGW, there are clearly ethical aspects too, such as those associated with the realisation that rich countries bear most of the responsibility for increased emissions of GHGs but are the least affectedw1. There are also energy considerations, and the question whether renewable sources of energy can replace fossil sources. Furthermore, economic considerations and political choices concerning climate change are closely related to energy options and greenhouse gas emissions.
The climate debate may indeed be one of the most profound issues of our time. It would be a shame if the broader public could not participate in this debate due to lack of understanding. Hence, it is important that schools teach students about climate and climate change, and that their information is accurate and up-to-date.
Web References
- w1 – For a discussion of the politics of climate change see www.OpenDemocracy.net
Review
Everyone has heard about climate change. The subject is frequently addressed by the media, but the information given is often incomplete or biased by political views. As science teachers, we have to provide students with correct information and instruments to develop critical attitudes based on facts and aimed at active citizenship.
This second of two articles by Rasmus Benestad is very useful because it presents the topic clearly and objectively, addressing the evidence for anthropogenic climate change.
I recommend this article to science teachers who are willing to update their knowledge and to secondary-school students interested in the facts and scientific evidence at the heart of this debate. The material is also particularly suitable for classroom discussion and for an interdisciplinary approach to environmental education in secondary schools.
Giulia Realdon, Italy





