Pete solare pe un Soare în rotație Teach article
Tradus de Gabriela Cîrstea. Studiem mișcarea oscilatorie armonică folosind imagini astronomice reale.
În urmă cu câțiva ani am descris în această publicație modul în care, folosindu-ne de lunile lui Jupiter, putem studia mișcarea oscilatorie armonică și am menționat intenția de a extinde proiectul la nivel internațional (Ribeiro, 2012). Această intenție a fost realizată, dar folosind un alt fenomen astronomic, și anume petele solare. În anii 2013 și 2014, studenți din Franța, Grecia, Italia, Polonia, Portugalia, România și Spania au participat la un proiect eTwinningw1 pentru a determina perioada de rotație a Soarelui cu ajutorul petelor solare. Ei au conceput propriile experimente, au pregătit rapoarte și au prelucrat date reale din baza de date a Observatorului Solar și Heliosferic (SOHO) gestionată de NASAw2.
Pornind de la proiectul lor, această activitate explică modul în care pot fi folosite ecuațiile mișcării oscilatorii armonice și imaginile petelor solare în contextul unei clase de elevi cu vârste cuprinse între 16 și 19 ani. Activitatea principală durează aproximativ o oră, dar există și idei de extindere pentru un proiect compus din mai multe lecții, și ați putea chiar să creați o rețea de clase, asemănătoare rețelei noastre.

Petele solare și mișcarea oscilatorie armonică
Petele solare sunt pete întunecate temporare pe suprafața Soarelui. Dacă presupunem că ele nu se mișcă, le putem folosi pentru a studia rotația Soarelui.
Observată de pe Pământ, o pată solară are o mișcare oscilatorie armonică. Acest termen este folosit pentru a descrie mișcări periodice regulate, cum ar fi cea a unui pendul sau oscilațiile unui obiect prins de un resort.
Pentru acest experiment puteți folosi imaginile petelor solare furnizate de SOHO (Observatorul Solar și Heliosferic), un observator spatial având misiunea de a explora Soarele, pornind de la nucleul și atmosfera acestuia, până la vântul solar.
Materiale
- Câteva imagini ale aceleiași pete solare, provenind din baza de date SOHO. În proiectul nostru am utilizat imagini luate la interval de o zi.
- Riglă
- Creion
- Hârtie milimetrică
- Calculator de buzunar
Procedeu
- Dacă realizați acest experiment ca parte a unui proiect mai amplu, ați putea începe la fel ca noi, invitându-vă elevii să studieze Soarele și petele solare: ce sunt ele și, eventual, ce legătură există între acestea și clima de pe Pământ și aurore.
Ca toate stelele, Soarele este un glob de plasmă fierbinte formată în principal din hidrogen ionizat supus fuziunii. În urma fuziunii, în nucleul Soarelui se generează energie, care este eliberată sub formă de radiație electromagnetică în atmosferă. Astfel se explică strălucirea Soarelui.
Petele solare apar atunci când concentrațiile cîmpului magnetic solar se opun convecției plasmei încărcate electric. Această convecție redusă micșorează temperatura la suprafață. În centrele întunecate ale petelor solare temperaturile scad la aproximativ 3700 K (față de 5700 K pentru restul suprafeței Soarelui), astfel că suprafața apare mult mai întunecată.
- Pentru a determina perioada de rotație a Soarelui folosind imagini ale unei pete solare din baza de date SOHO, fiecare grupă trebuie să măsoare cu o riglă deplasarea (x) – distanța de la pata solară respectivă la axa centrală a Soarelui – la diferite momente de timp (t).
- Grupele de elevi vor înregistra datele într-un tabel și vor nota deplasarea maximă posibilă (distanța de la axa de rotație la latura externă a imaginii Soarelui la latitudinea petei solare).
Mișcarea oscilatorie armonică poate fi interpretată ca proiecție pe o axă a unui obiect aflat în mișcare circulară uniformă. Altfel spus, fiind observat din lateral (echivalentul proiecției pe axa x), un obiect care se mișcă pe un cerc într-un plan orizontal, va descrie o mișcare periodică similară oscilației unui obiect prins de un resort. Doar dacă observăm obiectul de sus, mișcarea sa ne va apărea ca circulară. Trasând graficul acestei mișcări (distanța față de punctul central în funcție de timp) vom obține forma caracteristică unei dependențe sinusoidale (figura 1).
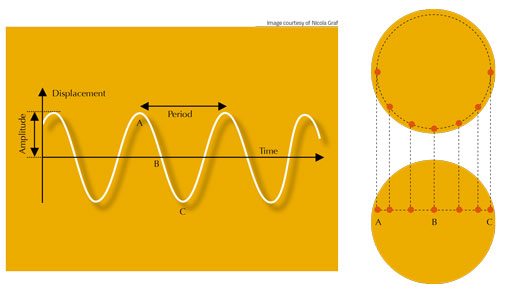
Pentru imaginea din dreapta, mulțumim lui Carla Isabel Ribeiro
Aceasta ar trebui să rezulte atunci când măsurăm deplasarea orizontală a petelor solare; ele par să se miște mai repede în apropierea axei de rotație din centrul Soarelui și mai lent pe măsură ce se apropie de laturile externe, de parcă ar fi atașate de un resort. Relația dintre cele două mișcări (oscilatorie armonică și circular uniformă) este reprezentată de ecuația:
x = Asin(ω t + φ) (1)
Unde x și A sunt elongația și, respectiv, amplitudinea mișcării pe traiectorie liniară a petelor solare văzute de pe Pământ. Mărimile fizice ω și φ sunt frecvența unghiulară și, respectiv, faza mișcării circulare văzute de la polul solar.
Deoarece frecvența unghiulară ω = 2π / T, unde T este perioada mișcării circulare, ecuația 1 devine:
x = Asin[(2π / T) t + φ] (2)
arcsin(x / A) = (2π / T)t + φ (3)
- Elevii vor calcula arcsin(x/A) pentru toate valorile lui x măsurate și apoi vor reprezenta graficul arcsin(x/A) în funcție de t (figura 2).
- Ei vor trasa apoi dreapta care corespunde cel mai bine datelor experimentale.
- Măsurând panta dreptei se va obține perioada de rotație a Soarelui. În exemplul de mai sus (figura 2), panta este de 0,01 radiani pe oră, deci T = 2π / ω = 628,3 ore = 26 zile.
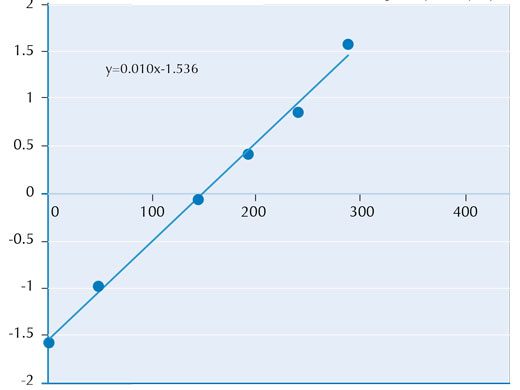
Pentru imagine, mulțumim lui Nikos Kyriazopulos
Extinderea activității
Dacă doriți să extindeți această activitate, fiecare elev poate repeta experimentul folosind imagini ale unei pete solare la alegere. De data aceasta ei vor măsura latitudinea petei solare, ceea ce le va permite să compare rotația Soarelui la diferite latitudini, comparând rezultatele lor cu cele obținute de ceilalți elevi.
Măsurarea rotației la diferite latitudini ar trebui să dovedească rotația diferențială a Soarelui: nefiind solid, perioada sa de rotație în apropierea polilor (aproximativ 34 de zile) este mai mare decât la ecuator (aproximativ 25 de zile). Discutați cu elevii posibile explicații ale acestui fapt.
Aveți idei de îmbunătățire a acestui proiect sau doriți să creați o rețea europeană similară, cu alte școli? Așteptăm comentariile dvs. referitoare la versiunea online a acestui articol.
References
- Ribeiro C (2012) Galileo and the moons of Jupiter: exploring the night sky of 1610. Science in School 25: 41–47.
Web References
- w1 – Portalul eTwinning este dezvoltat și administrat de European Schoolnet și este un spațiu virtual de întâlnire destinat schimbului de informații între școli.
- w2 – Puteți descărca date în timp real din baza de date a Observatorului Solar și Heliosferic (SOHO). SOHO este un proiect de cooperare internațională între Agenția Spațială Europeană și Administrația Aeronautică și Spațială Americană.
- w3 – Diferite metode utilizate de elevi pe parcursul proiectului sunt descrise chiar de ei pe site-ul MagazineFactory al proiectului.
Resources
- Pentru măsurarea deplasării petelor solare, participanții la proiectul nostru au folosit diferite metode, de la o simplă riglă sau trasarea unei grile pe imaginile Soarelui până la utilizarea unui software de procesare a imaginilor, toate acestea fiind descrise pe site-ul web al proiectuluiw3.
- Wikimedia Commons găzduiește câteva înregistrări video ale petelor solare, dintre care două surprind formarea și dezvoltarea petelor solare pe Soarele în rotație. Accesați http://commons.wikimedia.org or use the direct links.
- Pe site-ul web Alienworlds al Universității din Țara Galilor de Sud poate fi vizionată o animație care explică Soarele și petele solare. Accesați http://alienworlds.southwales.ac.uk sau folosiți linkul direct.
Review
Prea puțini tineri din zilele noastre au putut observa stelele pe cerul nopții, și același lucru este valabil și pentru petele solare, chiar dacă ele sunt un subiect fascinant și au jucat un rol în dezvoltarea astronomiei ca știință. (Dacă preferați să le vedeți cu propriii ochi, mai degrabă decât în imaginile din acest articol, puteți observa Soarele printr-o sticlă puternic opacizată sau în proiecție printr-un orificiu mic. Aveți grijă: observarea directă a Soarelui vă poate vătăma ochii. Este important de știut că pot fi observate puține pete solare pe parcursul lunilor sau chiar anilor.)
Dacă măsurați poziția orizontală a unei pete solare date pe parcursul unei zile, veți obține o fracțiune de ciclu al unei mișcări oscilatorii armonice. În acest articol, această informație este folosită pentru a obține perioada de rotație a Soarelui, iar rezultatele sunt surprinzătoare.
Eric Deeson, Marea Britanie





