Reglas de simetría Understand article
Traducido por Antonio Gallego. Todos saben lo que es la simetría. Pero en este artículo, Mario Livio, del Instituto Científico del Telescopio Espacial (STScI en inglés), Baltimore, USA, explica cómo pueden ser simétricas no solo las figuras, sino también las leyes naturales.
Todos se darán cuenta de que la mancha de tinta de la parte inferior izquierda es simétrica, pero pocos saben que la figura de la parte inferior derecha también se considera simétrica desde el preciso punto de vista matemático. ¿Qué es entonces realmente la simetría? ¿Y por qué ese concepto ha resultado tan fundamental que muchos científicos creen que es la base de las leyes naturales?


de tinta es simétrica…
Cuando cosas que podrían haber cambiado no lo hacen

mariposa
La simetría significa inmunidad a posibles alteraciones: la forman esos nucleos resistentes de ciertas figuras, frases, leyes o expresiones matemáticas que permanecen inalterables bajo determinadas transformaciones. Consideremos por ejemplo la frase «Se es o no se es»; es simétrica cuando se lee al revés, letra a letra; es decir, la sentencia se mantiene idéntica leída de atrás adelante. La misma propiedad tiene el título de la película Amor a Roma. Las frases con ese tipo de simetría se denominan palíndromos. Pues bien, los palíndromos juegan un importante papel en la estructura del cromosoma Y, que define el sexo de los machos. Hasta el 2003, los biólogos especialistas en el genoma creían que, dado que el cromosoma Y carece de compañero con el que intercambiar sus genes, su carga genética tendería a perderse debido a mutaciones que la dañaran. Mas para su sorpresa, los investigadores que secuenciaron el cromosoma Y descubrieron que ese cromosoma combate su destrucción usando palíndromos. Unos 6 millones de letras de su DNA (de un total de 50 millones) froman secuencias en forma de palíndromos. Estas copias-espejo proporcionan una copia de seguridad ante mutaciones perjudiciales y permiten que, en cierto sentido, ese cromosoma haga el sexo consigo mismo, pues ambas hileras pueden intercambiar su posición.
Para las figuras y formas bidimensionales, como las que se dibujan en un trozo de papel, existen exactamente 4 tipos de simetría «rígida» (o sea, sin permitir estiramientos ni distorsiones). Se conocen por los nombres de: reflexión, rotación, traslación y reflexión con deslizamiento.
La simetría de reflexión la hallamos por todas partes en nuestro alrededor: es la conocida simetría bilateral característica de los animales. Trácese una linea por la mitad de la foto de una mariposa (ver arriba). A continuación voltéese la foto manteniendo la línea central quieta. El perfecto solapamiento resultante indica que la mariposa permanece inalterable por una reflexión en torno a su eje central.

simetría rotacional
Muchas letras del alfabeto tienen también esa propiedad; por eso, si en un folio colocamos en columna (una debajo de otra) las letras AHIMTWX y ponemos un espejo al lado de ella, la imagen reflejada es idéntica a la columna original.
La simetría rotacional domina también mucho en la naturaleza. Un copo de nieve (ver arriba) girado 60, 120, 180, 240, 300 ó 360 grados (en torno al eje que pasa por su centro y es perpendicular a su plano) conduce a una configuración indistinguible de la original. También permanecerá inalterado un cículo girado un ángulo arbitrario entorno a su eje central perpendicular.
La simetría de traslación representa el tipo de inmunidad al cambio que encontramos en los motivos repetidos de forma periódica en figuras tales como la segunda. Traslación significa desplazamiento o salto, a una distancia determinada, a lo largo de una línea particular. Muchos frisos clásicos, los diseños de los papeles de pared, las filas de ventanas de los grandes edificios de apartamentos e incluso los ciempiés, todos exhiben este tipo de simetría.
La simetría de traslación representa el tipo de inmunidad al cambio que encontramos en los motivos repetidos de forma periódica en figuras tales como la segunda. Traslación significa desplazamiento o salto, a una distancia determinada, a lo largo de una línea particular. Muchos frisos clásicos, los diseños de los papeles de pared, las filas de ventanas de los grandes edificios de apartamentos e incluso los ciempiés, todos exhiben este tipo de simetría.

Todas las simetrías discutidas hasta ahora son simetrías de formas y figuras: aquellas que de hecho podemos ver con nuestros propios ojos. Las simetrías que subyacen a las leyes fundamentales de la naturaleza están íntimamente relacionadas con ellas; pero en lugar de centrarse en la forma o la figura, tienen que ver con una cuestión diferente: ¿qué transformaciones pueden realizarse en el mundo que nos rodea que dejen inalteradas las leyes que describen todos los fenómenos que observamos?
Reglas de simetría
Las «leyes naturales» en su conjunto describen un cuerpo de reglas que se supone que explican al pie de la letra todo lo que observamos en el universo. Que semejante enorme conjunto de reglas existiera era inconcebible antes del siglo XVII. Sólo gracias a las obras de gigantes de la ciencia como Galileo Galilei (1564-1642), René Descartes (1596-1650) y, en especial, Isaac Newton (1642-1727) resultó claro que un simple puñado de leyes podía explicar un extenso campo de fenómenos. De pronto, cosas tan diversas como la caída de las manzanas, las mareas en la playa y el movimiento planetario, todo quedaba cubierto por el paraguas de la ley de la gravitación de Newton.
De forma parecida, partiendo de los impresionantes resultados experimentales de Michael Faraday (1791-1867), el escocés James Clerk Maxwell (1831-1879) fue capaz de explicar con sólo cuatro ecuaciones toda la electricidad y el magnetismo clásicos, así como los fenómenos luminosos.
Esas leyes naturales se vio que obedecían algunas de las mismas simetrías que acabamos de encontrar y algunas otras pocas simetrías, algo más esotéricas. Ante todo, esas leyes son simétricas por traslaciones. La forma en que esa propiedad se manifiesta es muy sencilla: independientemente de que un experimento se realice en Nueva York o Los Ángeles, en el otro extremo de la Vía Láctea o en una galaxia a más de mil millones de años luz, los resultados podremos describirlos usando las mismas leyes. ¿Cómo sabemos que eso es verdad? Porque las observaciones sobre galaxias diseminadas por todo el universo muestran no sólo que la ley de la gravitación es la misma aquí y allí; también que los átomos de hidrógeno en los confines del universo obedecen con exactitud las mismas leyes del electromagnetismo y la mecánica cuántica que en la Tierra.
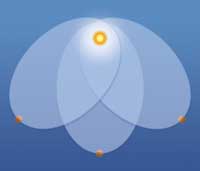
Newton es simétrica respecto
a las rotaciones, pero eso no
significa que lo sean las
órbitas
Las leyes naturales también son simétricas repecto a las rotaciones: esas leyes presentan exactamente la misma forma, tanto si medimos en dirección norte como en dirección a la cafetería más cercana. Es decir, la física no tiene direcciones preferentes en el espacio.
Si no fuera por esa notable simetría de las leyes por traslaciones y rotaciones, no habría esperanza de entender nunca las diferentes partes del cosmos. Más aún, incluso aquí en la Tierra, si esas leyes no fueran simétricas los experimentos habrían de repetirse en cada laboratorio por todo el globo.
Un palabra de cautela es necesaria para distinguir entre las simetrías de las figuras y las de las leyes. Los antiguos griegos pensaban que las órbitas de los planetas alrededor del sol eran simétricas respecto a las rotaciones: o sea, circulares. En realidad, esa no es la forma de las órbitas; sin embargo la ley de la gravitación de Newton sí es simétrica repecto a las rotaciones. Eso significa que las órbitas pueden ser (¡de hecho lo son!) elípticas, aunque sí pueden tener cualquier orientación en el espacio (ver arriba).
En el primer párrafo afirmé algo que es más fuerte que decir simplemente que las leyes obedecen ciertas simetrías. Dije que la simetría puede ser el origen de las leyes. ¿Qué significa eso?
El origen de las leyes naturales
Imagina que nunca antes habías oído hablar de los copos de nieve y que alguien te pide que lances una hipótesis sobre la forma de uno de ellos. Claramente se trata de un empeño imposible. Por lo que tú conoces, el copo de nieve lo mismo puede parecerse a una tetera que a la letra S que a Bugs Bunny.

copo de nieve
Incluso si te dieran la forma de uno de los rayos del copo de nieve (arriba, a) y te dijeran que es una parte de la figura completa, ello no te ayudaría mucho. El copo de nieve podría tener el aspecto de la configuración b (arriba). Por otra parte, si te dijeran que el copo de nieve es simétrico por rotaciones de 60 grados en torno a su centro, esa información sí podría usarse de forma muy eficiente. Esa simetría limita inmediatamente las posibles configuraciones a copos de nieve de seis, doce, dieciocho, etc esquinas. Asumiendo por experiencia que la naturaleza tiende a optar por la solución más simple y económica, una suposición muy razonable sería la del copo de nieve de seis esquinas (arriba, c). En otras palabras, la exigencia de simetría en la figura nos ha puesto en la dirección correcta.
En esa misma línea, la exigencia de que las leyes naturales sean simétricas repecto a ciertas transformaciones, no sólo dicta la forma de estas leyes; en ciertos casos, además, hace necesaria la existencia de fuerzas o nuevas partículas elementales. Dejad que me explique usando dos ejemplos de interés.
Uno de las principales metas de Einstein para su explicación de la relatividad general fue formular una teoría dentro de la cual las leyes naturales se presentaran exactamente igual para todos los observadores. Es decir, las leyes debían ser simétricas respecto a cualquier cambio de nuestro punto de vista espacio-temporal (en Física, esto se denomina «covarianza general»). Un observador sentado sobre la espalda de una tortuga gigante debería deducir las mismas leyes que uno montado en un tiovivo o en un cohete en plena aceleración. De hecho, si las leyes han de ser universales ¿por qué iban a depender de si el observador está o no acelerando?
Aunque la exigencia de simetría por parte de Einstein era ciertamente razonable, no era en absoluto trivial. Después de todo, un millón de traumatismos cervicales al año, sólo en Estados Unidos, prueba que sí notamos la aceleración. Y cada vez que un avión entra en un bache de aire, sentimos cómo el estómago se nos sube a la garganta. Parece pues haber una clara distinción entre movimiento uniforme y acelerado. ¿Cómo entonces las leyes naturales pueden ser las mismas para observadores en movimiento acelerado, cuando estos observadores parecen experimentar fuerzas adicionales?
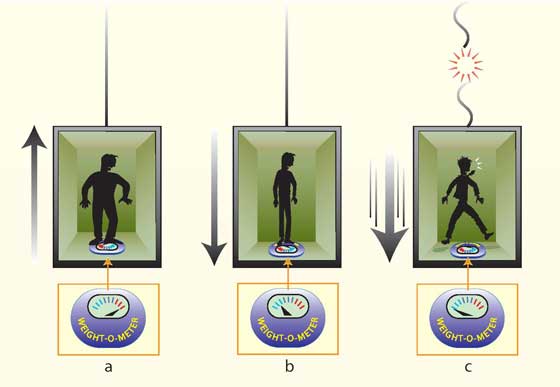
Consideremos la situación siguiente. Si te subes en una balanza de baño dentro de un ascensor que está acelerando hacia arriba, tus pies ejercen una gran presión sobre la balanza, que regristrará un peso mayor del real (arriba, a). Lo mismo sucedería, sin embargo, en un ascensor estático si la gravedad se hiciera más fuerte por algún motivo. Y un ascensor acelerando hacia abajo produciría la misma sensación que una gravedad más débil (arriba, b). Si el cable del ascensor se partiera, tú y la balanza caerías a la vez, en caida libre; y la balanza registaría peso cero (arriba, c). Así pues, la caída libre equivale a que alguien milagrosamente hiciera desaparecer la gravedad. Esto es lo que llevó a Einstein en 1907 a una realmente rompedora conclusión: la fuerza de la gravedad y la fuerza resultante de la aceleración son de hecho una y la misma. Esta potente unificación ha recibido el nombre de «principio de equivalencia» e implica que la aceleración y la gravedad son realmente dos facetas de una misma fuerza: son equivalentes.
En una conferencia impartida en Kyoto en 1922, Einstein describió así ese momento de revelación que tuvo en 1907: «Estaba sentado en la oficina de patentes, en Berna, cuando de repente se me ocurrió el siguiente pensamiento: si una persona está en caída libre ya no sentirá su propio peso. Estaba impresionado. Ese simple pensamiento me hizo una profunda impresión. Ello me impulsó a la teoría de la gravitación.”
El principio de equivalencia es en realidad la afirmación de una omnipresente simetría: las leyes naturales -tal como las expresan las ecuaciones de la relatividad general de Einstein- son las mismas en todos los sistemas, incluyendo a los sometidos a una aceleración. ¿Por qué entonces hay diferencias aparentes entre lo que se nota en un tio vivo y en un laboratorio en reposo? La teoría de la relatividad general da una respuesta sorprendente: Las diferencias se dan sólo en el entorno; no en las propias leyes. De forma parecida, las direcciones arriba y abajo, en la Tierra, parecen diferentes sólo por la gravedad terrestre; en sí mismas, las leyes naturales no tienen direcciones preferentes (son simétricas respecto a las rotaciones) y no distinguen el arriba y el abajo. En cuanto a los observadores situados en un tiovivo, sienten la fuerza centrífuga, que -según la relatividad general- es equivalente a la gravedad. La conclusión es verdaderamente electrizante: ¡la simetría de las leyes frente a cambios en las coordenadas espacio-temporales impone la existencia de la gravedad! Esto explica por qué la simetría es el origen de las fuerzas. La exigencia de simetría no le deja a la naturaleza ninguna opción: la gravedad tiene que existir.
Review
El Dr. Mario Livio, un Astrofísico Numerario del Instituto Científico del Telescopio Espacial, ofrece una explicación muy interesante de la simetría de las leyes naturales. Para las formas y figuras trazadas sobre un trozo de papel existen cuatro tipos de simetría: reflexión, rotación, traslación y reflexión con desplazamiento. ¿Cómo pueden aplicarse estas simetrías a las leyes naturales? ¿Las leyes naturales son simétricas? ¿Qué transformaciones pueden hacerse sobre ellas de forma que las leyes queden invariantes?
Aunque no está directamente relacionado con el curriculum de materias escolares, este artículo será seguramente de interés para todos los profesores de ciencias a los que les gustaría mejorar su comprensión de las leyes que gobiernan el universo. Los profesores de matemáticas podrían encontrar este artículo de especial interés.
Elton Micallef, Malta
